اسأل الساحر #119
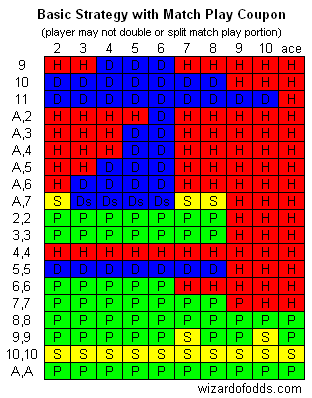
ما هي التغييرات التي يجب على المرء إجراؤها على استراتيجية البلاك جاك الأساسية عند لعب يد واحدة فقط عندما يكون الهدف هو زيادة فرصة الفوز بهذه اليد (على سبيل المثال عند استخدام قسيمة اللعب المطابق)؟
يعتمد ذلك على ما إذا كان يُسمح للاعب بمضاعفة وتقسيم رهان اللعب المطابق. عادةً لا يُسمح للاعب بذلك، مما يضره. يوضح الرسم البياني التالي كيفية تعديل استراتيجية المضاعفة والتقسيم، بافتراض عدم قدرة اللاعب على مضاعفة رهان اللعب المطابق، وإذا قسّم اللاعب رهانه، يُعتمد على أول يد لعب، بناءً على مجموعات أوراق لا نهائية واستقرار الموزع عند ورقة 17 ناعمة. استراتيجية "اضرب/اثبت" هي نفسها.
ما رأيك في الادعاء أدناه، بأن الله ديمقراطي كما يتضح من حقيقة أن جميع المقاطعات التي صوتت لصالح جور في عام 2000 نجت من الأعاصير الثلاثة التي ضربت فلوريدا مؤخرًا؟
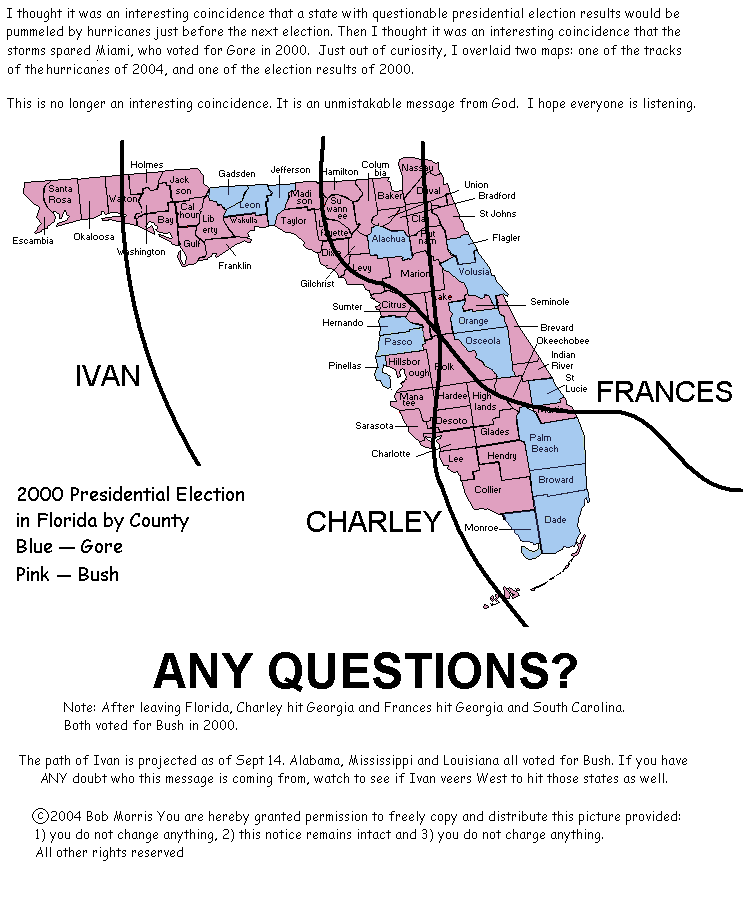
أولاً، أنشر هذا لأن المؤلف سمح بذلك في الأسفل. هذا مثال جيد على أن الارتباط لا يعني بالضرورة السببية. من السهل العودة بالزمن إلى الوراء والعثور على الكثير من المصادفات. لإثبات أي شيء، يجب طرح فرضية قبل جمع أي دليل.
متابعة (١٣ نوفمبر ٢٠٠٤): أشار قارئ آخر إلى أن هذه الخريطة كانت في البداية مزحة، ثم تحولت إلى أسطورة شعبية . وكما يشير هذا الرابط، فإن مسارات الأعاصير في الرسم البياني غير دقيقة، وأن الأعاصير ضربت العديد من مقاطعات غور. هذا يُظهر أنه لا يجب تصديق كل ما تقرأه، وخاصةً على الإنترنت.
أحب موقعك، شكرًا على كل الجهد المبذول فيه. أحاول النقر على بعض الإعلانات بين الحين والآخر، مع أنني لا أقيمر على الإنترنت.
(سأترك لرجل الإعلانات الخاص بي، مايكل بلو جاي، الإجابة على هذا السؤال.)
شكرًا لمحاولتك مساعدتنا، ولكن وفر نقراتك، فهي تُضيع وقتك ولا تُفيدنا بأي شكل. يدفع لنا مُعلنونا مبلغًا ثابتًا شهريًا، لذا نحصل على نفس المبلغ سواء نقرت أم لا. ولكن حتى لو حصلنا على أجرنا مقابل كل نقرة، فلن نطلب منك النقر على الإعلانات دون مُبرر، لأن ذلك لن يكون عادلًا للمُعلنين. يتوقع المُعلنون الذين يدفعون مقابل النقرات تحقيق أرباح من هذه النقرات، ويؤذيهم نقر المستخدمين دون نية الشراء. أينما كنت على الإنترنت، إذا كنت تعلم أن المُعلن يدفع مقابل النقرة، فمن غير اللائق أن تنقر على إعلانه إذا كنت تعلم أنك لا ترغب حقًا في الاطلاع على ما يُقدمه.
نحن نتميز بفرض رسوم شهرية على المعلنين. معظم إعلانات الكازينوهات الإلكترونية عبارة عن برامج تسويق بالعمولة، حيث يحصل مشرف الموقع على نسبة مئوية (حوالي 35%) من خسارة اللاعبين بعد فتح حساب. في الواقع، يُعدّ نشر مشرفي المواقع الأمريكية للإعلانات كبرامج تسويق بالعمولة أمرًا مشكوكًا فيه، وهذا أحد أسباب عدم قيامنا بذلك. سبب آخر هو أن لاعبينا يميلون إلى أن يكونوا أكثر تعليمًا وأقل عرضة للخسارة، مما قد يؤثر على عمولاتنا التسويقية. لذا، فإن السبب الرئيسي لعدم قيامنا ببرامج التسويق بالعمولة هو أننا لسنا مضطرين لذلك - بصفتنا أحد أبرز مواقع المقامرة على الإنترنت، يمكننا بيع الإعلانات بشروطنا الخاصة لأن العديد من الكازينوهات الإلكترونية تتسابق في محاولة الدفع لنا مقابل بعض مساحاتنا الإعلانية المحدودة. من الجيد أن نكون في الصدارة. :)
يسعدني أنك بدأت بلعب تكساس هولدم. أحب اللعبة وأفوز بها عبر الإنترنت، ولكن بصعوبة بالغة. قرأت أكثر من اثني عشر كتابًا عن البوكر، لكنني أردتُ معرفة رأيك في بعض النقاط.
- ما رأيك في "الوضع"؟ مثال: هل تعتقد أن هناك أوراقًا مربحة من الوضع المتأخر، ولكن لا ينبغي لعبها من الوضع المبكر؟
- ماذا عن "احتمالات الرهان"؟ أفهم المفهوم، لكنني راهنتُ على العديد من الأوراق التي كانت ستفوز، ببساطة لأنني لم أكن أملك الاحتمالات الصحيحة للبقاء والسحب... تشير الرسوم البيانية على موقعكم الإلكتروني إلى أن أقوى الأوراق الأولية لها "قيمة متوقعة" معينة إذا لم تُطوَ. هل تنصح بمتابعة هذه الأوراق حتى نهاية الرهان إلا إذا كان من الواضح أنك خسرت (بغض النظر عن احتمالات الرهان)؟
شكرا لك على وقتك.
أولاً، ما زلت مبتدئًا لذا لست الشخص الأفضل للسؤال. الموضع مهم جدًا في لعبة هول إم. كلما تأخر موضعك، زادت المعلومات التي لديك عن بطاقات خصومك بحلول دورك. على سبيل المثال، إذا قمت بإقران البطاقة الوسطى على الطاولة، وكانت لك علامة "تحقق" وأنت الأخير، فيمكنك أن تشعر بالراحة عند الرفع مع العلم أنه ربما لم يقترن أحد بالبطاقة العالية. ومع ذلك، سترى بحلول الوقت الذي يدور فيه الرهان حول الطاولة. إذا كانت لديك يد جيدة، ولكنها ليست رائعة، وقمت برفعها، فقد يعيد اللاعبون ذوو الأيدي الأقوى رفعها. إذا قمت بالتحقق مع مثل هذه اليد، فقد يتم التحقق منها بالكامل وتفوتك فرصة بناء الرهان وتخويف اللاعبين الآخرين. لذلك لا تراهن بقيمة بطاقاتك الخاصة فقط، بل عليك بدلاً من ذلك أن تزنها مقابل بطاقات أي شخص آخر. كلما تأخرت في اللعب، ستعرف المزيد عن بطاقات اللاعب الآخر بحلول دورك.
احتمالات الرهان مفهوم مهم. وكما هو الحال في أي نوع من المقامرة، تعتمد قيمة الرهان على احتمالية فوزك، ومبلغ الرهان، ومقدار الربح. يوضح الجدول التالي بعض الحالات الشائعة. يوضح عمود الاحتمالات احتمالية الحصول على ستريت أو فلش. بينما يوضح عمود احتمالات الرهان الحد الأدنى لعدد وحدات الرهان الموجودة في الرهان ليكون رهانًا جيدًا، بافتراض أنك ستفوز بالتأكيد إذا حصلت على يدك (إلا إذا كان لديك فلش نوت، فهذا شرط أساسي).
السحوبات المتكررة
| يُسلِّم | بعد | احتمالية صناعة اليد | احتمالات الرهان |
|---|---|---|---|
| 4 إلى تدفق | فشل | 34.97% | 1.86 |
| 4 إلى مستقيم خارجي | فشل | 31.45% | 2.18 |
| 4 إلى مستقيم داخلي | فشل | 16.47% | 5.07 |
| 4 إلى تدفق | دور | 19.57% | 4.11 |
| 4 إلى مستقيم خارجي | دور | 17.39% | 4.75 |
| 4 إلى مستقيم داخلي | دور | 8.70% | 10.50 |
هناك العديد من العوامل الأخرى التي يجب مراعاتها. يمكن كتابة كتاب كامل عنها، وفي الواقع فعل الكثيرون ذلك. أنصح شخصيًا بكتاب "Get the Edge at Low-Limit Texas Hold 'em" لبيل بيرتون ككتاب تمهيدي عن لعبة البوكر. أما بالنسبة لجداولي، فلا أثق مطلقًا في يد بداية جيدة طوال الوقت. ستكون هناك مرات عديدة تحتاج فيها إلى طيّ زوج من الآسات. طاولاتي مصممة لمساعدة اللاعب فقط على المراهنة قبل الفلوب. بعد الفلوب، من المرجح أن تتغير القيمة المتوقعة ليدك بشكل كبير.
هل يؤثر اللعب المجاني في كازينو على الإنترنت على اللعب بأموال حقيقية؟ أعتقد ذلك بالتأكيد، لكنني أردتُ الاستفسار منك.
لا ينبغي ذلك. وأضمن أن أي إعلان كازينو على هذا الموقع يُمارس لعبة عادلة. أي كازينو أجد فيه غشًا، سواءً كان للمتعة أو بأموال حقيقية ، لن أتردد في إضافته إلى قائمتي السوداء .
مرحباً يا ساحر، أردتُ معرفة إن كان بإمكانك الإجابة على هذا السؤال. في لعبة قمار شهيرة في فرنسا في القرن السابع عشر، كان اللاعب يرمي نرداً ٢٤ مرة. يفوز برهانه إذا كانت إحدى هذه الرميات على الأقل رقم ستة مزدوج. كان هناك جدلٌ آنذاك حول ما إذا كان احتمال الفوز أعلى أم أقل من ٥٠٪. هل يمكنك مساعدتي؟
بالتأكيد، هذا سهل. احتمال ظهور رقم ١٢ مرة واحدة على الأقل في ٢٤ رمية هو ١-(٣٥/٣٦) ٢٤ = ٤٩.١٤٪. لذا، فإن الاحتمالات ترجح المراهنة ضد الرقم ١٢. هذا رهان ذكي لأن العدد المتوقع لأرقام ١٢ في ٢٤ رمية هو ٢/٣. مع ذلك، هذا لا يعني أن احتمال ظهور الرقم ١٢ هو ٢/٣، لأنه في بعض الأحيان قد يكون هناك أكثر من رقم ١٢ واحد، واللاعب الذي يراهن على الرقم ١٢ لا يفوز بأي أرقام ١٢ إضافية بعد الرمية الأولى. إذا كان احتمال الفوز في أي محاولة هو ص، وعدد المحاولات هو ن، واحتمال الفوز مرة واحدة على الأقل هو و، فإن حل قيمة n بدلالة ص و و يعطينا...
w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n*log(1-p)
n= log(1-w)/log(1-p)
في مثالنا، n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051. لذا، إذا كانت احتمالية النجاح 50% في 24.6 رمية، فيجب أن تكون أقل قليلاً في 24 رمية.
هل هناك أي المقامرين المحترفين الحقيقيين هناك؟
نعم، الكثير منهم. أعرف العديد منهم شخصيًا. أحاول أن أصبح واحدًا منهم، لكن برأيي، يتطلب الأمر رأس مال لا يقل عن ثلاثة أضعاف دخلك السنوي المعتاد، ولم أصل إلى هذا الحد بعد. للاطلاع على قصص حقيقية لبعض أفضل المقامرين المحترفين، أنصح بقراءة كتاب "سحرة المقامرة" لريتشارد دبليو. مونشكين.
ما هو احتمال الحصول على 1،2،3،4،5،6 باستخدام ستة أحجار نرد، ست مرات على التوالي؟
يمكن التعبير عن احتمالية الحصول على العدد ١٢٣٤٥٦ بستة أحجار نرد في رمية واحدة على النحو التالي: احتمال (عدم تطابق النرد الثاني مع النرد الأول) * احتمال (عدم تطابق النرد الثالث مع النرد الأول أو الثاني) * ... = ١*(٥/٦)*(٤/٦)*(٣/٦)*(٢/٦)*(١/٦) = ٠٫٠١٥٤٣٢. وبالتالي، فإن احتمالية حدوث ذلك ست مرات متتالية هي ٠٫٠١٥٤٣٢. ٦ = ١ في ٧٤٫٠٣٧٫٢٠٨٫٤١١.


