اسأل الساحر #227

قبل ثلاث سنوات، في عمود "اسأل الساحر "، كتبتَ: "أنت محقّ في أن 500 رمية قليلة جدًا لإثبات صحة تأثير النرد أو عدمه، لكن 500 رمية أفضل من لا شيء". هل يمكنك وصف ما تحتاجه من شخص يُزعم أنه مؤثر على النرد، في تجربة، لتشعر بالثقة الكافية للبدء بالمراهنة عليه بمبالغ طائلة؟ أسأل لأن مليار جولة تُعدّ معيارًا جيدًا للنتائج "الموثوقة" في بعض ألعاب محاكاة البلاك جاك. مع التصميم التجريبي الأكثر كفاءة (أي الذي يتطلب أقل عدد من الرميات) الذي يمكنك تخيله، كم عدد الرميات التي يحتاجها اللاعب ليكون واثقًا من تأثيره على النتائج؟ أعلم أن الإجابة ستعتمد على مهارة اللاعب، لكنك تفهم قصدي. إذا كنت بحاجة إلى مليون رمية حتى في أفضل الأحوال، فلن يكون الأمر مجديًا.

Myooligan من Greenfelt

لا توجد نقطة حاسمة تُكتسب عندها الثقة. إنها مسألة درجة. أولًا، أود أن أسأل عن طبيعة الاختبار، وما يتوقعه مطلق النار. في أي اختبار، هناك خطأان محتملان. قد يفشل مطلق نار ماهر بسبب سوء الحظ، أو قد ينجح مطلق نار عشوائي بسبب حسن الحظ. من بين الاثنين، أُفضّل تجنب النتيجة الإيجابية الخاطئة. أعتقد أن الاختبار المعقول سيُحدد احتمال النتيجة السلبية الخاطئة بحوالي 5%، واحتمال النتيجة الإيجابية الخاطئة بحوالي 1%.

على سبيل المثال، لنفترض أن المُدّعي يقول إنه يستطيع الحصول على متوسط سبعة نقاط كل سبع رميات للنرد. سيُلقي مُقامر عشوائي نقطة واحدة كل ست رميات في المتوسط. بالتجربة والخطأ، أجد أن الاختبار الذي يُلبي هذين المعيارين هو رمي النرد ٣٦٠٠ مرة، ويتطلب ٥٤٧ نقطة أو أقل للنجاح، أو نقطة واحدة لكل ٦.٥٨ رمية.

يُفترض أن يُحرز رامي واحد من كل سبعة رميات 514.3 رمية سباعية، بانحراف معياري قدره 21.00. باستخدام التقريب الغاوسي، فإن احتمال أن يُحرز رامي ماهر 548 رمية سباعية أو أكثر (نتيجة سلبية خاطئة) هو 5.7%. أما الرامي العشوائي، فيُفترض أن يُحرز رمية سباعية في المتوسط 600 رمية، بانحراف معياري قدره 22.36. أما احتمال اجتياز رامي عشوائي للاختبار (نتيجة إيجابية خاطئة) فهو 0.94%. يُظهر الرسم البياني أدناه النتائج المحتملة للرماة المهرة والعشوائيين. إذا كانت النتائج على يسار الخط الأخضر، فسأعتبر الرامي قد اجتاز الاختبار، وسأراهن عليه.

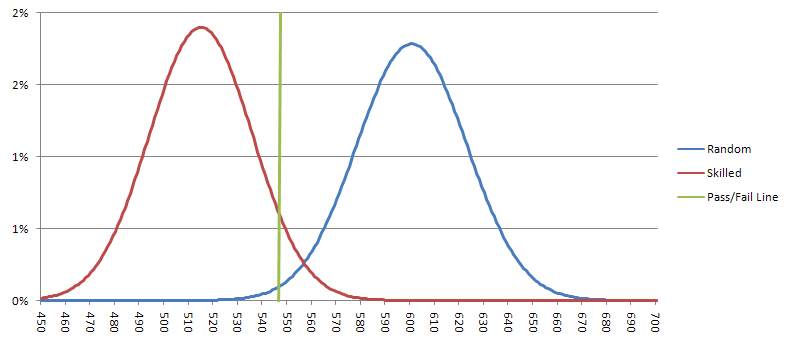
المعضلة العملية هي أنه إذا افترضنا رميتين في الدقيقة، فسيستغرق إجراء الاختبار 30 ساعة. ربما يمكنني أن أكون أكثر مرونة بشأن مستوى الدلالة، لتقليل الوقت المطلوب، لكن النتائج لن تكون بنفس القدر من الإقناع. أعتقد أن الوقت قد حان لاختبار أكبر من تجربة وونغ التي أجريت 500 رمية.

إذا تم لعب رهان "السيدة المحظوظة" الجانبي فقط عندما يكون العدد الحقيقي، مثلاً، ١٠ أو أكثر، فهل يمكن التغلب على هامش الكازينو؟ إذا كان الأمر كذلك، فما هو الحد الأدنى للعدد الحقيقي الذي يمكن عنده التغلب على هامش الكازينو بهذا الرهان الجانبي؟

Julie Jacques من Morristown, TN

لم أدرس تأثير عدّ البطاقات في هذا الرهان بنفسي. مع ذلك، قام أرنولد سنايدر بذلك، ويمكن الاطلاع على نتائجه في كتابه "الكتاب الكبير للبلاك جاك" . ينصح سنايدر بالمراهنة في لعبة بستة مجموعات أوراق إذا كانت المجموعة الأخيرة من البطاقات، وكان العدد +10 أو أكثر، باستخدام عدد السبعات الحمراء. أما في لعبة بمجموعتين من البطاقات، فينصح بالمراهنة على المجموعة الأخيرة، وكان العدد +6 أو أكثر.

ما هي الفائدة التي تعود على اللاعب عندما يسمح الكازينو بالاستسلام المتأخر في لعبة ورق من 6 مجموعات، وعندما يصل الكازينو إلى 17 ناعمة، وعندما يقف الكازينو عند 17 ناعمة؟ ماذا عن لعبة ورق من 8 مجموعات؟

Sam من Las Vegas

يمكنك إيجاد إجابات لمثل هذه الأسئلة باستخدام حاسبة هامش الربح الخاص بي، وذلك بتغيير قاعدة معينة وملاحظة تأثير ذلك على هامش الربح. عادةً ما أطلب منك القيام بذلك، لكنني في مزاج صبور اليوم، لذا إليك:

6 مجموعات، الموزع يقف على 17 ناعمة: 0.0726%
8 مجموعات، الموزع يقف على 17 ناعمة: 0.0758%
6 مجموعات، ضربات الموزع على 17 ناعمة: 0.0882%
8 مجموعات، ضربات الموزع على 17 ناعمة: 0.0916%

كنت أتساءل عما إذا كانت هناك طريقة لحساب متوسط عدد المحاولات التي قد تستغرقها خسارة عشر وحدات من أي نقطة معينة، الرهان على اللاعب في الباكارات.

J.J. من Oceanside, CA

نسبة ربح الكازينو على رهان اللاعب هي ١٫٢٣٥١٪، بافتراض وجود ثماني مجموعات أوراق. العدد المتوقع للأيدي اللازمة لخسارة عشر وحدات هو ١٠/٠٫٠١٢٣٥١ = ٨٠٩٫٦٦.

كنتُ مؤخرًا ألعب بوكر منزليًا (أوماها ديوسيس وايلد) مع بعض أفراد عائلتي. كان هناك خمسة لاعبين، وتراجع عددهم إلى اثنين. كنتُ واحدًا من الاثنين. كان اللاعب الآخر يفوز طوال الليل. وأخيرًا، حصلتُ على يد جيدة. نظرتُ إليها وقلتُ ساخرًا "أربعة سبعات". قالت إن لديها أربعة آسات، وبدأت بجمع الرقائق. ثم صحّحتُ نفسي، وأخبرتُها أن لديّ ستريت فلش. ثم أخبرتني أنني فزتُ بأربعة سبعات. أظهرتُ لها يدي، لكنها أصرت على أنني فزتُ بأربعة سبعات، وأن يدي لم تعد جيدة. إذًا، السؤال هو: من فاز باليد؟ من الواضح أن ستريت فلش أفضل من أربعة متماثلة. ولكن هل أفسدتُ يدي بقول ما قلته؟ لا يزال المال على الطاولة.

Don من Lihue, HI

في النهاية، البطاقات تتحدث. كان من المفترض أن تفوز بتلك اليد.