اسأل الساحر #253
لا أفهم كيف يكون ترتيب A-7 في جداول القوة الخاصة بلعبة Texas Hold 'Em أقل من ترتيب KJ المناسب، ولكن على الآلة الحاسبة الخاصة بك يكون احتمال فوز A7 أعلى.
سؤال جيد. لفائدة القراء الآخرين، إليكم احتمالات الفوز بيد عشوائية مع كلٍّ من هاتين اليدين الابتدائيتين في لعبة لاعبين:
KJ متناسقة ضد A-7 غير متناسقة
| يُسلِّم | يفوز | يخسر | يرسم | القيمة المتوقعة |
ك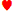 ج ج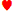 | 0.6148 | 0.3634 | 0.0218 | 0.2513 |
أ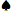 7 7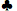 | 0.5717 | 0.3949 | 0.0334 | 0.1768 |
ومع ذلك، وفقًا لحاسبة Texas Hold 'em للاعبين اثنين، فإن احتمالات مواجهة هاتين اليدين لبعضهما البعض هي:
فوز A7 = 53.52%
فوز KJ = 46.10%
التعادل = 0.39%
لذا، فإنّ تصنيف KJ المتناسب أعلى في جدولي، ولكنه أدنى من تصنيف A7 غير المتناسب. لماذا؟
يصعب شرح الإجابة. عند مواجهة يدين، يجب مراعاة كيفية تفاعلهما. على سبيل المثال، في جدول قوة اليد الابتدائية، تتفوق ورقة AK غير المتماثلة على ورقة AQ غير المتماثلة بفارق ضئيل، بقيم متوقعة 0.3064 و0.2886 على التوالي. مع ذلك، إذا واجهتهما، فإن ورقة AK تتفوق على ورقة AQ، كما يلي:
فوز AK = 71.72%
فوز AQ = 23.69%
التعادل = 4.58%
في لعبة A7-غير متماثلة مقابل لعبة KJ-متماثلة، يتفوق الآس على الملك والولد. تكون أكبر فرصة لفوز لاعب KJ إذا جمع K أو J معًا ولم يظهر أي آسات. أُظهر أن احتمال ذلك هو 37.73% فقط. أما النسبة المتبقية (46.10%) لاحتمال فوز KJ فتأتي من الأيدي الأعلى.
على الرغم من أن A7 قوية ضد KJ، إلا أنها غالبًا ما تهيمن عليها الأيدي العشوائية أكثر من KJ.
ربما تكون هذه مقارنة سيئة، لكنها أشبه بلعبة حجر ورقة مقص . بين اللاعبين المهرة، يُفترض أن يكون لكل رمية قوة متقاربة. مع ذلك، إذا رمى أحد اللاعبين ورقة والآخر مقصًا، فلن يكون لقوة الرميتين أي معنى، وسيفوز المقص.
في بيغهورن ولونغهورن بلاس فيغاس، يُسمح بمضاعفة الرهان بثلاث بطاقات في البلاك جاك. هل هناك أي تغييرات في الاستراتيجية يجب عليّ إجراؤها بموجب هذه القاعدة؟
يقول أحد قراء موقع Wizard of Vegas الخاص بي أنه يجب إجراء التغييرات التالية، فيما يتعلق باستراتيجية تعدد الأوراق القياسية حيث يحصل الموزع على 17 ناعمة:
- ضربة ناعمة 13 مقابل 5 أو 6
- ضرب بطاقتين ناعمتين 15 مقابل 4
- ضربة 3،3 مقابل 2
سبب اختيار الأيدي الضعيفة هو إمكانية الحصول على ضعف ضعيف أفضل بعد الضربة. قيمة الحصول على الثلاثيات أعلى بموجب هذه القاعدة، لأن الحصول على الآس يُعدّ ضعفًا جيدًا بثلاث بطاقات.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
إذا تم رمي العملة المعدنية 100 مرة، ما هو احتمال الحصول على سلسلة من 7 وجوه على التوالي على الأقل مرة واحدة على الأقل؟
إذا كان هناك تعبير سهل وغير متكرر للإجابة، فأنا لست على علم به. مع ذلك، هناك إجابة سهلة ومتكررة.
f(n)= pr(الذيل في التقلب الأول)×f(n-1) +
pr(الوجه في الرمية الأولى، الكتابة في الرمية الثانية)×f(n-2) +
pr(الوجه في أول رميتين، الكتابة في الرمية الثالثة)×f(n-3) +
pr(الوجه في أول 3 رميات، الكتابة في الرمية الثالثة) × f(n-4) +
pr(الوجه في أول 4 رميات، الكتابة في الرمية الرابعة) × f(n-5) +
pr(الوجه في أول 5 رميات، الكتابة في الرمية الخامسة) × f(n-6) +
pr(الوجه في أول 6 رميات، الكتابة في الرمية السادسة) × f(n-7) +
pr(الرؤوس في أول 7 تقلبات) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
أين:
f(n)=احتمال النجاح في غضون n تقلبات.
pr(x)=احتمال حدوث x.
جداول البيانات مثالية لمثل هذه المسائل. في لقطات الشاشة لجدول البيانات أدناه، وضعتُ احتمالًا يساوي 0 للخلايا من B2 إلى B8، لأنه لا يمكن الحصول على 7 صور متتالية في 6 عمليات قلب أو أقل. بالنسبة للخلية B9، وضعتُ الصيغة التالية:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
ثم نسختها ولصقتها من الخلية B10 إلى الخلية B102، وهو ما يعادل 100 انعكاس. هذا الاحتمال هو 0.317520. وقد أكدته محاكاة عشوائية.
 |  |
بعد نشر هذا المقال، شاركني ريك بيرسي حله لجبر المصفوفات. إليكم الحل بكلماتي الخاصة. أفترض أن القارئ على دراية بأساسيات جبر المصفوفات.
أولاً، هناك ثماني حالات محتملة يمكن أن تكون فيها الزعنفة في أي نقطة:
p 1 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 7 رؤوس أخرى من النقطة الحالية.
p 2 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 6 رؤوس أخرى من النقطة الحالية.
ص 3 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 5 رؤوس أخرى من النقطة الحالية.
ص 4 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 4 رؤوس أخرى من النقطة الحالية.
ص 5 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 3 رؤوس أخرى من النقطة الحالية.
ص 6 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى رأسين إضافيين من النقطة الحالية.
ص 7 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى رأس واحد إضافي من النقطة الحالية.
ص 8 = احتمال النجاح، مع العلم أنك لا تحتاج إلى المزيد من الرؤوس = 1.
لنُعرّف الحد الأقصى للرقم S n بأنه احتمالية وجوده في كل حالة بعد الرمية رقم n. يمثل S 0 الاحتمالات قبل الرمية الأولى، حيث تكون نسبة وجوده في الحالة 0 100%. إذًا، S 0 =
| 1 0 0 0 0 0 0 0 |
دع T تكون مصفوفة التحويل من تقلبتين متتاليتين، أو S n إلى S n+1 ، حيث S n+1 = T × S n
- إذا كنت في الحالة 1، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 2 (مع وجود وجه)، وفرصة 0.5 للبقاء في الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 2، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 3 (مع وجود وجه)، وفرصة 0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 3، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 4 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 4، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 5 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 5، فبعد رمية واحدة لديك فرصة 0.5 لتكون في الحالة 6 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 6، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 7 (مع وجود وجه)، وفرصة 0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 7، فبعد رمية واحدة لديك فرصة 0.5 لتكون في الحالة 8 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 8، فقد حققت النجاح، وستبقى في الحالة 8 باحتمالية 1.0.
وضع كل ذلك في شكل مصفوفة الانتقال T =
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
للوصول إلى احتمال كل حالة بعد قلب واحد...
(1) S 1 = S 0 × T
ماذا عن بعد الانقلابين؟
(2) S 2 = S 1 × T
دعونا نستبدل المعادلة (1) في المعادلة (2)...
(3) S 2 = S 0 × T × T = S 0 × T 2
ماذا عن بعد 3 تقلبات؟
(4) S 3 = S 2 × T
استبدال المعادلة (3) في (4)...
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
يمكننا الاستمرار في القيام بذلك حتى الوصول إلى الحالة التي نصل إليها بعد الانقلاب رقم 100...
S 100 = S 0 × T 100
إذن، ما هو T 100 ؟ قبل ظهور الحواسيب، كان من الصعب جدًا فهم هذه الأمور. مع ذلك، باستخدام دالة MMULT في برنامج Excel، ومع كثرة النسخ واللصق، نجد أن T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
يوضح لنا المصطلح الموجود في أعلى اليمين احتمالية وجودنا في الحالة 8 بعد 100 عملية رمي، وهو 0.317520.
أطلق كازينو توسكانا مؤخرًا عرضًا ترويجيًا، حيث ستحصل على مكافأة قدرها 100 دولار أمريكي إذا ربحت 30 بلاك جاك خلال 30 يومًا. في البداية، كان الحد الأدنى للرهان 5 دولارات أمريكية للحصول على ختم بطاقتك. ولكن، سمعت لاحقًا أن الحد الأدنى للختم قد ارتفع إلى 15 دولارًا أمريكيًا. كتبتُ شكوى إلى مدير الكازينو بشأن هذا الأمر، ذكرتُ فيها جزئيًا:
أردتُ فقط التعبير عن خيبة أملي من هذا التغيير، إن كان صحيحًا. لم تسنح لي الفرصة للاستفادة من العرض الترويجي، وأشك في قدرتي على ذلك الآن. يبدو الوقت اللازم للحصول على 30 بلاك جاك (قيل لي إنه حوالي 8 ساعات من اللعب المتواصل) غير معقول بسعر 15 دولارًا لليد، بينما لا يزال العرض الترويجي يقدم 100 دولار فقط.
وهذا هو الرد الذي وصلني:
ردًا على رسالتك الإلكترونية بشأن عرض بلاك آوت في لعبة البلاك جاك، لست متأكدًا من مصدر معلوماتك حول المدة التي يستغرقها إكمال بطاقة بلاك آوت. لقد لاحظنا لاعبين يُكملون البطاقة في أقل من أربع ساعات. لديك أيضًا ثلاثون يومًا لإكمالها. آمل أن تفهم أن هذه المهمة ليست مستحيلة مع هذا الوقت الطويل. شكرًا لك على رسالتك. يسرّنا سماع آراء عملائنا. نأمل أن تُجرّبها وتربح بعض المال!
ما هو احتمال الحصول على 30 بلاك جاك في أربع ساعات؟
وفقًا لمقارنتي للعبة ، يلعب لاعبو البلاك جاك حوالي 70 يدًا في الساعة. احتمال الفوز في لعبة بستة رزم هو 24 × 96 / مجموع (312،2) = 4.75%. أفترض أن التعادل في البلاك جاك سيُحسم أيضًا. لذا، من المفترض أن يستغرق ملء البطاقة حوالي 30 / 0.0475 = 632 يدًا، أي 9.02 ساعة.
احتمال ملء البطاقة خلال ٤ ساعات، بافتراض ٢٨٠ يدًا، هو ١ من ٣٠٠٠٠ عند لعب يد واحدة في كل مرة. أظن أن أي لاعب يحقق هذا الهدف خلال أربع ساعات كان يلعب يدين على الأقل في كل مرة.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .


