اسأل الساحر #261
ما هي العوامل المؤثرة على إجمالي مراهنات كرة القدم مع استمرار الموسم، وتدهور الأحوال الجوية، وتوافر المزيد من المعلومات حول أداء الفرق في الآونة الأخيرة؟ ما مدى سهولة (أو صعوبة) اكتشاف الأخطاء في الخط؟
للمساعدة في الإجابة على هذا السؤال، قمت بإعداد رسم بياني لمتوسط النقاط المسجلة حسب رقم الأسبوع في دوري كرة القدم الأميركي، استنادًا إلى كل موسم من عام 1983 إلى عام 2009. يوضح الرسم البياني التالي النتائج.
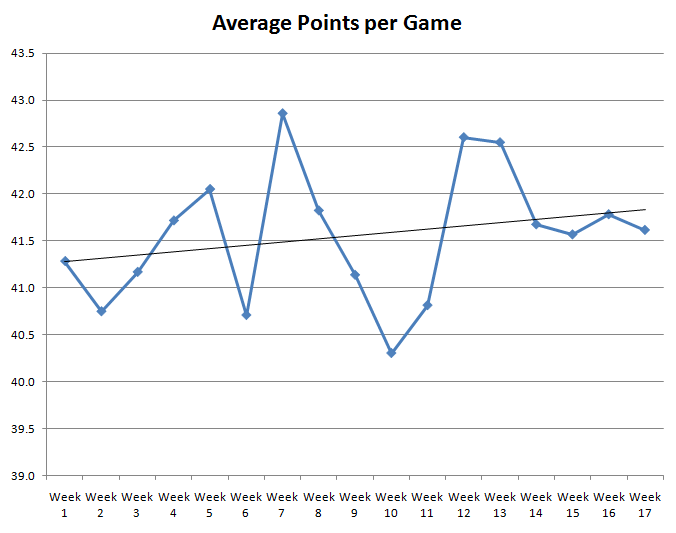
كما ترون، يرتفع الخط وينخفض كثيرًا. الخط الأسود الرفيع هو خطّ أفضل ملاءمة، وهو يُظهر اتجاهًا عامًا تصاعديًا. لذا، مع تقدّم الفصول وانخفاض درجات الحرارة، يرتفع متوسط النقاط المُسجّلة بشكل طفيف، ولكن قد يكون هذا ببساطة تغيّرًا عشوائيًا.
هذا كل ما أستطيع قوله. للحصول على رأي عام حول تأثير الطقس على المراهنات الرياضية بشكل عام، توجهتُ إلى صديقي جيسون بين، الخبير في هذا المجال. إليكم ما قاله:
في معظم الحالات، تكون الرياح هي الجانب السائد للطقس الذي يؤثر بشكل كبير على اللعبة؛ ولكنها ليست الوحيدة. في لعبة البيسبول وغيرها من الرياضات الخارجية، يمكن أن يكون للظلال تأثير متساوٍ، وخاصة خلال مباريات البيسبول في فترة ما بعد الظهيرة في بداية الموسم وأواخره. المطر أو الثلج ليس عاملاً كبيرًا كما يعتقد معظم الناس في كرة القدم، لأنه يؤثر بشكل عام على كل من الهجوم والدفاع بالتساوي. على سبيل المثال سيكون هناك ظهير دفاعي ضد مستقبل واسع. سيبطئ المطر والثلج من سرعتهما بالتساوي، وبالتالي لا يمنح أي من الجانبين أفضلية. يمكن للرياح ببساطة أن تقضي على لعبة التمرير في كرة القدم إلى جانب الركل. لقد رأيت مباريات حيث أُجبر فريق التمرير على تشغيل الكرة في كل لعبة تقريبًا بسبب الرياح العرضية القوية. لا يحدث هذا كثيرًا، ولكن في بعض الأحيان تكون الرياح هي الحاسمة النهائية للعبة.تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
ماذا يحدث عادة في لعبة الكرابس إذا قام اللاعب بالمراهنة بأكثر من مضاعفات الاحتمالات في لعبة الكرابس، ولم يلاحظ الموزعون ذلك حتى يفوز الرهان أو يخسر؟
سألتُ مديرًا سابقًا لألعاب الطاولة في فيغاس عن هذا الأمر. قال إن نسبة احتمالات الرهان، التي تزيد عن المضاعف المسموح به لرهان الخط، ستُدفع عند نقطة الرهان. طُرح هذا السؤال ونوقش في منتدى موقعي المرافق "ساحر فيغاس" .
في دوري كرة القدم الأميركي، في المتوسط، ما هو احتمال أن يكون الفريق الآخر هو التالي في التسجيل بعد تسجيل هدف؟
استنادا إلى مواسم دوري كرة القدم الأميركي من عام 2000 إلى عام 2009، فإن الإجابة هي 57%.
لنفترض وجود مبارزة ثلاثية (ترويل) بين المشاركين أ، ب، ج. يتقاتلون حتى الموت من أجل امرأة. جميعهم رجال، ويتفقون جميعًا على القواعد التالية.
- يشكل المشاركون الثلاثة مثلثًا.
- كل واحد منهم لديه رصاصة واحدة فقط.
- أ يبدأ أولا، ثم ب، ثم ج.
- احتمالية إصابة الهدف المقصود هي 10%.
- احتمالية إصابة B للهدف المقصود هي 60%.
- احتمالية إصابة C للهدف المقصود هي 90%.
- لا يوجد إطلاق نار عرضي.
- إطلاق النار في الهواء (عمدا) وإطلاق النار على نفسك مسموح به، وهما دائما ناجحان.
- إذا بقي اثنان أو ثلاثة ناجين بعد أي جولة، يُعطى كلٌّ منهم رصاصة جديدة. ثم يتناوبون على إطلاق النار، بنفس الترتيب، متجاوزين أي شخص مات سابقًا.
- كل المشاركين الثلاثة هم منطقيون مثاليون.
من يجب أن يستهدفه أ في البداية؟ ما احتمال نجاته من كل هدف أولي؟
نُوقش هذا اللغز في برنامج "مثير للاهتمام للغاية" على قناة بي بي سي. مرر لأسفل ١٠٠ سطر للعثور على الإجابة والحل.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
إليكم احتمالات فوز اللاعب (أ) وفقًا لكل هدف أولي. كما ترون، يتعاظم احتمال فوز اللاعب (أ) بإطلاق النار في الهواء عمدًا.
احتمالات ترويل
| الاستراتيجية | احتمال الفوز |
| هواء | 13.887% |
| أ | 0.000% |
| ب | 12.560% |
| ج | 13.094% |
للحل، لنستخدم الرمز Pr(X) للدلالة على احتمال بقاء المجموعة X فقط بعد الجولة. ولنستخدم المصطلح Pr(X*) للدلالة على احتمال فوز المجموعة X بالجولة في النهاية، بعد تكرار اللعبة حتى تتغير حالة اللعبة بإصابة أحد اللاعبين. لنفترض أن Pr(X**) هو احتمال أن يكون اللاعب X هو الناجي الوحيد. لإيجاد الاحتمالات النهائية، لننظر أولًا إلى حالتي اللاعبين. من الواضح أن كلًا منهما سيُصيب الآخر.
أ مقابل ب
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
إذا نجا كلاهما، فسيتكرر الأمر حتى يبقى ناجٍ واحد فقط. لذا، تكون احتمالات أن يكون الناجي الأخير هي:
- العلاقات العامة(A*) = العلاقات العامة(A)/(1- العلاقات العامة(AB)) = 0.1/0.64 = 0.15625
- العلاقات العامة(B*) = العلاقات العامة(B)/(1- العلاقات العامة(AB)) = 0.54/0.64 = 0.84375
أ مقابل ج
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
إذا نجا كلاهما، فسيتكرر الأمر حتى يبقى ناجٍ واحد فقط. لذا، تكون احتمالات أن يكون الناجي الأخير هي:
- العلاقات العامة(A*) = العلاقات العامة(A)/(1- العلاقات العامة(AC)) = 0.1/0.91 = 0.10989011
- العلاقات العامة(C*) = العلاقات العامة(B)/(1- العلاقات العامة(AC)) = 0.81/0.91= 0.89010989
ب مقابل ج
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
إذا نجا كلاهما، فسيتكرر الأمر حتى يبقى ناجٍ واحد فقط. لذا، تكون احتمالات أن يكون الناجي الأخير هي:
- العلاقات العامة(B*) = العلاقات العامة(A)/(1- العلاقات العامة(BC)) = 0.6/.96 = 0.625
- العلاقات العامة(C*) = العلاقات العامة(B)/(1- العلاقات العامة(BC)) = 0.36/.96= 0.375
الآن، نحن مستعدون لتحليل حالة اللاعبين الثلاثة. لننظر إلى الحالة التي يستهدف فيها اللاعب (أ) اللاعب (ب).
ثلاثة لاعبين - أ يهدف إلى ب
إذا أصابت الكرة أ الكرة ب، فإن الكرة ج ستنجو حتمًا، وقد تصيب الكرة أ أو لا تصيبها. لذا، فإن نتيجتين محتملتين لإصابة الكرة ب هما AC وC. إذا أخطأت الكرة أ الكرة ب، فإن الكرة ب ستستهدف الخطر الأكبر ج. إذا أصابت الكرة ب الكرة ج، فإن الكرة أ و B ستنجو. إذا أخطأت الكرة ب الكرة ج، فإن الكرة ج ستستهدف الخطر الأكبر ب. إذا أخطأت الكرة ج الكرة ب، فإن الكرة الثلاثة ستنجو. إذا أصابت الكرة ج الكرة ب، فإن الكرة أ و C ستنجو. لذا، فإن النتائج المحتملة هي C، AB، AC، وABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.1 × 0.9 = 0.09. يتحقق ذلك بضرب A لـ B، ثم ضرب C لـ A.
- Pr(AB) = 0.9 × 0.6 = 0.54. يتحقق ذلك بفشل A في الوصول إلى B، ثم اصطدام B بـ C.
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334. يمكن تحقيق ذلك بطريقتين. الأولى: أن يصطدم A بـ B، ثم يفوت C A. الثانية: أن يفوت A B، ثم يفوت B C، ثم يصطدم C بـ B.
- Pr(BC) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. يتحقق ذلك من خلال فقدان جميع القيم الثلاث.
وبنفس المنطق الذي اتبعناه في حالات اللاعبين، يمكننا قسمة كل نتيجة على (1-Pr(ABC))=0.964 لإيجاد احتمالات كل حالة، على افتراض أن حالة اللعبة تغيرت بعد الجولة.
- العلاقات العامة(C*) = 0.09/0.964 = 0.093361.
- العلاقات العامة (AB*) = 0.54/0.964 = 0.560166.
- العلاقات العامة (AC *) = 0.334 / 0.964 = 0.346473.
من خلال اللعب بين لاعبين، نعلم أنه إذا انتهى الأمر بفوز أ و ب، فسيفوز أ باحتمال 0.15625، وب باحتمال 0.84375. وإذا انتهى الأمر بفوز أ و ج، فسيفوز أ باحتمال 0.109890، وج باحتمال 0.890110.
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. يمكن أن يكون A هو الفائز بطريقتين: (1) الوصول إلى حالة AB، ثم الفوز، أو (2) الوصول إلى حالة AC ثم الفوز.
- Pr(B**) = 0.560166 × 0.84375 = 0.472640. سيكون B هو الفائز إذا وصل إلى حالة AB، وعندها يفوز B.
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760. يمكن لـ C الفوز بفوز A على B، ثم فوز C على A في الجولة الأولى، أو بوصوله إلى حالة AC، ثم فوز C.
لذا، إذا كانت استراتيجية أ هي استهداف ب في البداية، فإن احتمال كونه الناجي الوحيد هو 12.56%.
ثلاثة لاعبين - أ يهدف إلى ج
إذا أصابت الكرة أ الكرة ج، فإن الكرة ب ستنجو حتمًا، وقد تصيب الكرة أ أو لا تصيبها. لذا، فإن نتيجتين محتملتين لإصابة الكرة ج هما: أ ب و ب. إذا أخطأت الكرة أ ج، فإن الكرة ب ستستهدف الخطر الأكبر ج. إذا أصابت الكرة ب ج، فإن الكرة أ و ب ستنجو. إذا أخطأت الكرة ب ج، فإن الكرة ج ستستهدف الخطر الأكبر ب. إذا أخطأت الكرة ج ب، فإن الكرة الثلاثة ستنجو. إذا أصابت الكرة ج ب، فإن الكرة أ و ج ستنجو. لذا، فإن النتائج المحتملة هي: ب، أ ب، أ ج، أ ب ج، أ ب ج.
- Pr(A) = 0.
- Pr(B) = 0.1 × 0.6 = 0.06.
- Pr(C) = 0.
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58. يمكن تحقيق ذلك بطريقتين.الأول هو أن يضرب أ ج، ثم يخطئ ب أ. الثاني هو أن يخطئ أ ب، ثم يخطئ ب ج.
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324. يتحقق ذلك بأن A يفتقد C، وB يفتقد C، وC يصطدم بـ B.
- Pr(BC) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. يتحقق ذلك من خلال فقدان جميع القيم الثلاث.
وبنفس المنطق الذي اتبعناه في حالات اللاعبين، يمكننا قسمة كل نتيجة على (1-Pr(ABC))=0.964 لإيجاد احتمالات كل حالة، على افتراض أن حالة اللعبة تغيرت بعد الجولة.
- العلاقات العامة (ب*) = 0.06/0.964 = 0.062241.
- العلاقات العامة (AB*) = 0.58/0.964 = 0.601660.
- العلاقات العامة (AC *) = 0.324 / 0.964 = 0.336100.
بنفس منطق الحل لحالة A يهدف إلى B:
- العلاقات العامة(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943.
- العلاقات العامة (ب**) = 0.062241 + 0.601660 × 0.84375 = 0.569891.
- العلاقات العامة(C**) = 0.336100 × 0.890110 = 0.299166.
لذا، إذا كانت استراتيجية أ هي استهداف ج في البداية، فإن احتمال كونه الناجي الوحيد هو 13.09%.
ثلاثة لاعبين - أخطأ عمدًا
بعد أن يُخطئ أ عمدًا، سيُصوِّب ب على التهديد الأكبر ج. إذا أصاب ب ج، فسينجو أ و ب. إذا أخطأ ب ج، فسيُصوِّب ج على التهديد الأكبر ب. إذا أخطأ ج ب، فسينجو الثلاثة جميعًا. إذا أصاب ج ب، فسينجو أ و ج. إذن، النتائج المحتملة هي أ ب، أ ج، أ ب ج.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0.6. يتحقق ذلك باصطدام B بـ C.
- Pr(AC) = 0.4 × 0.9 = 0.36. يتحقق ذلك بفقدان B لـ C، ثم اصطدام C بـ B.
- Pr(BC) = 0.
- Pr(ABC) = 0.4 × 0.1 = 0.04. يتحقق ذلك من خلال فقدان جميع القيم الثلاث.
وبنفس المنطق الذي اتبعناه في حالات اللاعبين، يمكننا قسمة كل نتيجة على (1-Pr(ABC))=0.96 لإيجاد احتمالات كل حالة، على افتراض أن حالة اللعبة تغيرت بعد الجولة.
- Pr(AB*) = 0.6/0.96 = 0.625.
- Pr(AC*) = 0.36/0.96 = 0.375.
بنفس منطق الحل لحالة A يهدف إلى B:
- العلاقات العامة(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865.
- العلاقات العامة (ب**) = 0.625 × 0.84375 = 0.527344.
- العلاقات العامة(C**) = 0.375 × 0.890110 = 0.333791.
لذا، إذا كانت استراتيجية أ هي استهداف ج في البداية، فإن احتمال كونه الناجي الوحيد هو 13.89%.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .


