اسأل الساحر #265

أنت تخلط بين المتوسط الحسابي والوسيط. لنأخذ حالتي كمثال. أنا رجل أبلغ من العمر 45 عامًا. متوسط عمري المتوقع هو 78.11 عامًا، ومع ذلك، لديّ فرصة 50.04% للوصول إلى سن الثمانين.

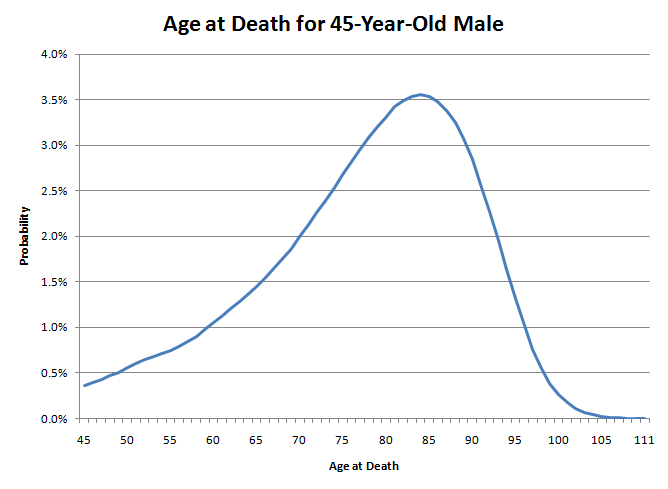
سيكون عمري عند الوفاة أشبه برمي سهم على هذا الرسم البياني. لاحظ كيف أن الذيل الأيسر أعرض بكثير من الأيمن. هذا يعني أن احتمال وفاتي الآن منخفض جدًا. ومع ذلك، مع تقدمي في العمر، سيستمر احتمال الوفاة في العام المقبل في الارتفاع. على سبيل المثال، بالنسبة لرجل يبلغ من العمر 45 عامًا، فإن احتمال البقاء على قيد الحياة حتى سن 46 مرتفع جدًا بنسبة 99.64%. ومع ذلك، في سن 85، فإن احتمالية الوصول إلى سن 86 هي 89.21% فقط. الأمر أشبه بغرز الطبيعة سكينًا في ظهرك ببطء. في البداية قد لا تقتلك، ولكن مع مرور كل عام، تزداد احتمالية ذلك تدريجيًا. ومع ذلك، بمجرد أن تصل إلى أواخر السبعينيات، تقول الطبيعة كفى من الألعاب وتبدأ في إغراقك بها.

إذا راهن عدد كبير من الرجال البالغين من العمر 45 عامًا على هذا الرسم البياني، فإن 49.96% منهم سيُصيبون بين 45 و79 عامًا، و50.04% سيصيبون بين 80 و111 عامًا. مع ذلك، فإن النصف المحظوظ الذي يصل إلى يمين الرسم البياني لن يعيش على الأرجح أكثر من 80 عامًا. بمجرد أن يصل الرجل إلى 80 عامًا، يتوقع أن يعيش 7.78 عامًا إضافية فقط. في الوقت نفسه، سيموت الكثير من النصف غير المحظوظ الذي لا يصل إلى 80 عامًا في سن أصغر بكثير. لذا، فإن الوفيات الكثيرة في سن الشباب هي التي تُخفض متوسط العمر المتوقع.

في موقف مماثل، ضع في اعتبارك حجر نرد مرقم 10، 20، 30، 31، 32، 33. المتوسط هو 26، ولكن هناك فرصة 2/3 للحصول على رقم أكبر من ذلك.

كمثال على اختلاف المتوسط الحسابي والوسيط، لنفترض أننا أضفنا حالتي وفاة إلى العينة. إحداهما في سن 46 والأخرى في سن 81. لن يتغير احتمال الوصول إلى سن 80، لكن متوسط العمر المتوقع عند سن 45 سينخفض.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

سؤال جيد. تنص طريقة الكازينو على تقسيم خمسة آسات، مع وضع آسين في اليد المنخفضة. الاستثناء هو الاحتفاظ بالخمسة المتشابهة في اليد العالية إذا كان بإمكانك وضع ملكين في اليد المنخفضة. تشير صفحة باي غاو بوكر الخاصة بي إلى سبعة طرق كازينو من لاس فيغاس وأتلانتيك سيتي، وجميعها تشمل هذا الاستثناء. أما الثلاثة من خارج هاتين المدينتين فلا تشملهما.

احتمال الحصول على أربعة آسات، وجوكر، وملكين هو ١ من ٢٥,٦٩٠,٥١٣. بافتراض أن الموزع يُراهن، فإن الحالة الوحيدة التي يُفيد فيها هذا الاستثناء هي إذا كان لدى اللاعب أربعة متماثلة أو أكثر في يده العليا. احتمال ذلك هو حوالي ١ من ٣٠٠. واحتمال حدوث كليهما هو حوالي ١ من ٧.٦ مليار.

وفقًا لمجلس مراقبة الألعاب في ولاية نيفادا، كان هناك 306 طاولة بوكر باي غاو في نيفادا في عام 2009. إذا افترضنا بسخاء 60 يدًا في الساعة، ولاعبين لكل طاولة، وكل طاولة مفتوحة على مدار الساعة طوال أيام الأسبوع، فسيستغرق الأمر 23.7 عامًا حتى يحدث هذا الاستثناء ويحدث فرقًا في النتيجة.

لذا، تُلزم الكازينوهات كل موزع في لعبة باي غاو بوكر بحفظ هذا الاستثناء، مع أنه ربما لم يُحدث فرقًا في النتيجة في تاريخ اللعبة. أعتقد أن الشخص الذي فكّر في إضافة هذه القاعدة هو نفسه الذي قرر أن السلسلة A2345، المعروفة باسم "العجلة"، هي ثاني أعلى سلسلة متتالية.

هذه مسألة شائعة في تاريخ علم الاحتمالات. يعتقد الكثيرون خطأً أن الإجابة هي 18، لأن احتمال الحصول على 12 هو 1 من 36، و18×(1/36)=50%. ومع ذلك، ووفقًا لهذا المنطق، فإن احتمال الحصول على 12 في 36 رمية هو 100%، وهو أمر غير صحيح تمامًا. إليك الحل الصحيح. ليكن r هو عدد الرميات. احتمال ألا تكون الرمية 12 هو 35/36. احتمال وجود 0 رميات 12 في r رمية هو (35/36) ^r . لذا، علينا إيجاد r في المعادلة التالية:

(35/36) ^r = 0.5
log(35/36) ^r = log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
ر = 24.6051

إذن، لا توجد إجابة تقريبية. احتمال الحصول على ١٢ في ٢٤ رمية هو ١-(٣٥/٣٦) ^٢٤ = ٤٩.١٤٪. واحتمال الحصول على ١٢ في ٢٥ رمية هو ١-(٣٥/٣٦) ^٢٥ = ٥٠.٥٥٪.

إذا أردتَ المراهنة على هذا، فلنفترض أنك تستطيع الحصول على ١٢ في ٢٥ رمية، أو أن شخصًا آخر لا يستطيع ذلك في ٢٤ رمية. في كلتا الحالتين، ستكون لديك أفضلية عند تساوي المبلغ.

أراهن بنسبة ١٠ إلى ١ على حصولك على المال، مع أنهم قد يتحدثون معك قليلًا أولًا. سبب شكوكي هو أن مكتب المراهنات الرياضية يمكنه إلغاء رهانٍ يبدو أنه خاطئ، بإذن من مجلس مراقبة الألعاب.

"لا يجوز لأي كتاب إلغاء أي رهان من جانب واحد دون الحصول على موافقة كتابية مسبقة من رئيس مجلس الإدارة." -- لائحة نيفادا رقم 22.115

مع أن هذا الحق موجود، إلا أنه نادرًا ما يُستخدم بناءً على أدلة غير مباشرة. أخبرني بما سيحدث.

ملاحظة: أبلغني السائل لاحقًا أنه حصل على راتبه دون أي مشاكل تذكر.

نعم، سيحدث ذلك بعد ^{١٠٠,٠٠٠} -١ ثانية. راجع موقعي mathproblems.info ، المسألة ٢٠٦، لحلين.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .