اسأل الساحر #267

ما هي الاستراتيجية المثلى لتقسيم أموالك في برنامج المسابقات Million Dollar Money Drop، إذا لم تكن متأكدًا من الإجابة؟

Anon E. Mouse

ولصالح القراء الآخرين، دعوني أراجع القواعد أولاً.

يبدأ فريق اللاعبين بمبلغ 1,000,000 دولار.
يتم إعطاء الفريق سؤال اختياري متعدد.
على الفريق تقسيم أمواله على الإجابات المحتملة. أي مبلغ يُجمع على الإجابة الصحيحة ينتقل إلى السؤال التالي.
يجب على الفريق استبعاد إجابة واحدة على الأقل تمامًا من خلال عدم وضع أي أموال عليها.
تتكرر هذه العملية لعدة جولات. يُمنح اللاعب أيضًا فرصة واحدة لتغيير رأيه.

من البديهي أنه إذا كان الفريق متأكدًا من الإجابة، فعليه المراهنة بكل أمواله على الإجابة الصحيحة. إذا تمكن الفريق من تضييق نطاق الإجابة إلى اثنتين، مع منح كل منهما فرصة ٥٠٪ للصواب، فعليه تقسيم أمواله بالتساوي بين الخيارين.

يصبح الأمر أكثر صعوبة إذا مال الفريق نحو إجابة واحدة دون استبعاد إجابة واحدة أو أكثر من الإجابات الأخرى تمامًا. لنأخذ مثالًا. لنفترض أن الفريق حدد احتمال كل إجابة صحيحة كما يلي: أ ١٠٪، ب ٢٠٪، ج ٣٠٪، د ٤٠٪. كيف يُقسمون أمواله؟

أعتقد أن الحل يكمن في اتباع معيار كيلي . باختصار، يجب على الفريق تعظيم قيمة لوغاريتم ثروته مع كل سؤال. للقيام بذلك، عليك مراعاة مقدار ثروتك الحالية.

لنفترض أن ثروتك الحالية، التي جمعتها بشكل مستقل عن البرنامج، تبلغ 100,000 دولار. هذا هو سؤالك الأول، لذا لديك مليون دولار من أموال البرنامج لتقسيمها. استبعد أولًا الخيار الأقل احتمالًا، بما يتوافق مع قواعد البرنامج. ثم تريد تعظيم 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000)، حيث تشير الأحرف الصغيرة a وb وc إلى الجزء المخصص لكل إجابة.

يمكن حل هذه المسألة باستخدام حساب التفاضل والتكامل وحل معادلة ثلاثية الحدود، أو التجربة والخطأ، أو -كما أُفضّل- خاصية "البحث عن الهدف" في برنامج إكسل. أيًا كان الحل الذي تستخدمه، فالإجابة الصحيحة هي وضع 18.9% على الخيار ب، و33.3% على الخيار ج، و47.8% على الخيار د.

بالطبع، لن يتمكن أيٌّ من المشاركين في البرنامج من إجراء كل هذه العمليات الحسابية في الوقت المسموح به، ناهيك عن حاجتك لنقل كميات كبيرة من النقود خلال ذلك الوقت. نصيحتي العملية هي تقسيم المبلغ بما يتناسب مع تقديرك لاحتمالية صحة الإجابة، بافتراض أن الخيار الأقل احتمالاً غير وارد. في هذا المثال، سيؤدي ذلك إلى تقسيم المبلغ بنسبة 22.2% على الخيار (ب)، و33.3% على الخيار (ج)، و44.4% على الخيار (د).

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

سمعتُ عن كازينو يفترض فيه، إذا خسر الموزع، فوز جميع اللاعبين المتبقين. تُوزّع اللعبة مكشوفة، باستثناء البطاقات ذات المكافأة المضاعفة التي تُوزّع مقلوبة. لذا، إذا تسببت البطاقة ذات المكافأة المضاعفة في خسارة اللاعب، ولكن خسر الموزع أيضًا، يفوز اللاعب. يفعل الكازينو هذا لأنه يخشى من عدّاد البطاقات، ولا يريد أن يرى اللاعبون بطاقات يعتقدون أنها غير مهمة. ما هي الاستراتيجية الأساسية الصحيحة في ظل هذه القاعدة، وما هي نسبة ربح الكازينو؟

Kellynbnf

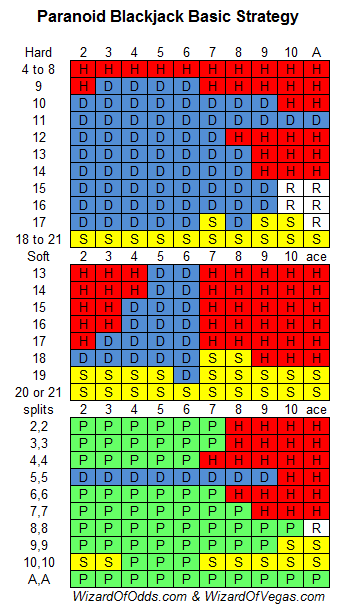
سأفترض وجود ست مجموعات أوراق، وأن الموزع يحصل على ١٧ ناعمة، ثم مضاعفة بعد التقسيم، ثم الاستسلام، وإعادة تقسيم الآسات. إذا كان المضاعفة لأقل من ذلك غير مسموح، فإن أفضلية اللاعب ستكون ٤.٩٪. هذه هي الاستراتيجية الصحيحة. من الواضح أن هذه الاستراتيجية قد تُثير بعض علامات الاستفهام.

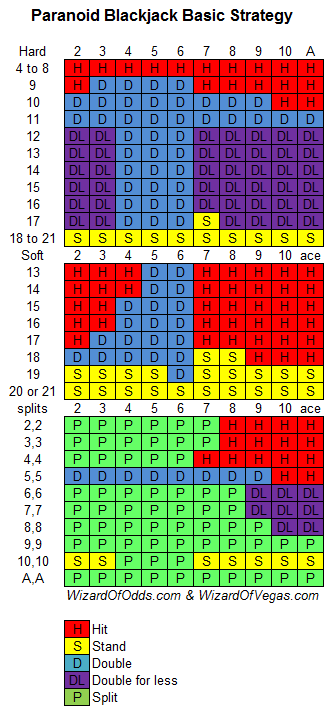
إذا كان الرهان المضاعف على مبلغ أقل مسموحًا، فإنني أحصل على ميزة قصوى للاعب بنسبة 9.4% باتباع الاستراتيجية التالية. عند الرهان المضاعف على مبلغ أقل، راهن بأقل مبلغ إضافي ممكن، ويفضل أن يكون بنسًا واحدًا فقط. نسبة الـ 9.4% التي أعتمدها تفترض رهانًا مضاعفًا صغيرًا. في الواقع، تشترط معظم الكازينوهات المضاعفة على الأقل عند الحد الأدنى للطاولة.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

في كازينو فيينا، يوجد رهان جانبي في لعبة البلاك جاك. تستخدم اللعبة ست مجموعات من الأوراق، ويعتمد الموزع على ورقة ١٧ ناعمة. يُدفع ٥ إلى ٢ في حال خسارة الموزع، بغض النظر عن نتيجة الرهان الأصلي.

churn

تم إعداد ملحق البلاك جاك 2B الخاص بي لأسئلة كهذه. يُظهر هذا الملحق أن احتمال خسارة الموزع هو 28.19% بموجب هذه القواعد، ما يجعل هامش ربح الكازينو 1.33%.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

في عمودك بتاريخ ١٤ ديسمبر ٢٠١٠، كتبتَ أن اليد AAAAAKK، المذكورة تحديدًا في أسلوب الكازينو، ربما لم تحدث قط في تاريخ اللعبة. ووفقًا لتاجر آخر، حصل لاعب على هذه اليد في محطة مين ستريت في نوفمبر ٢٠١٠.

PaiGowDan

مثير للاهتمام. كما كتبتُ، أقدّر أن هذه الظاهرة ستحدث مرة كل ٢٣.٧ عامًا تقريبًا في أي مكان في نيفادا. أعتقد أن تلك كانت إحدى تلك المرات.