اسأل الساحر #270

أُبيّن أن قيمة إعادة التقسيم اللانهائي، مقارنةً بالتقسيم حتى أربع أيادٍ كحد أقصى، تبلغ 0.05% إذا طُبّقت القاعدة على جميع الأزواج، بما في ذلك الآسات، و0.02% إذا لم تشمل الآسات. طُرح هذا السؤال ونوقش في منتدى موقعي المرافق "ساحر فيغاس" .

أرى أن احتمالات فوز VCU بالبطولة في Pinnacle هي: نعم +604 لا -750. لنحسب المبلغ الذي يجب أن تراهن به ضد فوز VCU لضمان فوز متساوٍ في كلتا الحالتين، وما هو هذا الفوز. لنفترض أن x هو الرهان. نتيجة الفوز = 50,000 - x.
نتيجة الخسارة = س * (١٠٠/٧٥٠) = (٢/١٥) س. ساوِ هذه القيم: ٥٠٠٠٠ - س = (٢/١٥) س ٥٠٠٠٠ = (١٧/١٥) س = ٥٠٠٠٠ × (١٥/١٧) س = ٤٤١١٧.٦٥ دولارًا. لنرَ إن كان هذا صحيحًا... إذا فازت جامعة فرجينيا كومنولث، فسيكون الناتج ٥٠٠٠٠ دولار ناقصًا من فندق هيلتون ناقص ٤٤١١٧.٦٥ دولارًا، ليصبح مجموع ما تحصل عليه من فندق بيناكل ٥٨٨٢.٣٥ دولارًا. أما إذا لم تفز جامعة فرجينيا كومنولث، فلن تحصل على أي شيء من فندق هيلتون، ولكن رهان بيناكل سيدفع ٤٤١١٧.٦٥ دولارًا × (١٠٠/٧٥٠) = ٥٨٨٢.٣٥ دولارًا. مع ذلك، أشك في أن الرهان ضد جامعة فرجينيا كومنولث سيدفع احتمالات عادلة. إذا كان المالك يخشى المخاطرة بشدة، وكان حريصًا على بيع التذكرة، فأعتقد أن سعر 6000 دولار أمريكي سيكون سعرًا عادلًا. مع ذلك، سأعتمد احتمال فوز VCU على خط +604، مما يعني أن احتمال الفوز 100/704 = 14.2%. هذا يعني أن قيمة التذكرة ستبلغ حوالي 7100 دولار أمريكي. كل هذا يتجاهل الآثار الضريبية. طُرح هذا السؤال ونوقش في منتدى موقعي المرافق "ساحر فيغاس" .

يبدو أنه لا توجد يد لا تُقهر عند عدم المراهنة. لذا، لننظر إلى يدين. الأولى لا يُمكن التغلب عليها أو التعادل في الرهانات العالية. والثانية لا يُمكن التغلب عليها أو التعادل في الرهانات المنخفضة.

(1) AAAAW/KK (W=برية)

لا يمكن التغلب على الآسات الخمسة في المجموعة العالية، ولكن يمكن تعادل زوج الملوك في المجموعة المنخفضة. عدد التركيبات التي تحتوي على ملكين هو كومبين (44،5) = 1,086,008. إجمالي عدد التركيبات المكونة من 7 بطاقات من أصل 46 بطاقة متبقية هو 53,524,680. لذا، فإن احتمال وجود ملكين هو 1,086,008/53,524,680 = 2.03%. مع العديد من هذه التركيبات، لن يلعب الموزع KK في المجموعة المنخفضة. وفقًا لملحق باي غاو بوكر 1 ، سيكون لدى الموزع زوج من الآسات أو أقل في المجموعة العالية بنسبة 74.93% من الوقت. هذا يعني أنه سيُكوّن زوجين أو أكثر، مما يسمح له بلعب الملوك في المجموعة المنخفضة بنسبة 25.07% من الوقت. وبالتالي فإن احتمال حصول اللاعب على ملكين، وقدرته على لعبهما في المستوى المنخفض، هو 2.03% × 25.07% = 0.51%، أو 1 من 196.

(2) AWQJT (ملائم)/AA

يمكن ربط الورقة الملكية في الأعلى، ولكن لا يمكن التغلب على الآسات أو ربطها في الأسفل. هنا أستخدم البرية لاستبدال الملك لصنع ورقة ملكية، ولكن كان من الممكن أيضًا أن تحل محل Q أو J أو T. لا أريدها أن تحل محل الآس، لأنه عندئذٍ سيكون هناك آسان متبقيان في المجموعة ليتمكن الموزع من ربط الورقة المنخفضة. بهذه الطريقة، لا يمكن للموزع ربط الورقة الملكية العالية إلا بورقة ملكية أخرى. ما هي احتمالات ذلك؟ هناك ثلاث بدلات متبقية للورقة الملكية، ويمكن أن تكون البطاقتان الأخريان أي شيء. لذا فإن عدد التركيبات التي تدفع هي 3 × combin(41,2) = 2,460. أحصل على 41 من 46 بطاقة متبقية في المجموعة بعد أن أزال اللاعب 7 من 43 الأصلية، ثم أطرح 5 أخرى للبطاقات الخمس في الورقة الملكية للموزع. لدينا combin(46,7) = 53,524,680 في المقام. لذا فإن احتمالات التعادل مع wild royal/AA هي 2,460/53,524,680 = 0.004596%، أو 1 من 21,758.

قبل أن يكتب لي أحدُ مُحبي الكمال، قد تكون هناك بعض المواقف الغريبة التي لا يلعب فيها الموزع الأوراق بالطريقة التي كنتُ أقصدها. لا أسعى للحصول على احتمال دقيق لكل حالة، بل لأُثبت لماذا أعتقد أن يد وايلد رويال/AA هي أفضل يد يُمكن الحصول عليها في باي غاو بوكر عند عدم المراهنة.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

1/2.

إذا استخدمنا لعبة الكينو للمقارنة، فسيكون لدى كل شخص 40 جينًا، كل منها مُمَثَّل بكرة كينو. ومع ذلك، سيكون لكل كرة رقم فريد. عندما يتزاوج شخصان غير مرتبطين، يكون الأمر أشبه بدمج 80 كرة بينهما في وعاء، واختيار 40 جينًا عشوائيًا لنسل التزاوج.

عندما خُلقت، حصلت على نصف الكرات في القادوس، وضاع النصف الآخر. عندما خُلقت، حصل أخوك أو أختك على نصف الكرات المسحوبة عند ولادتك، والنصف الآخر غير المسحوب. لذا، فأنتما متطابقان وراثيًا بنسبة ٥٠٪. وللسبب نفسه، إذا سُحبت ٤٠ رقمًا في لعبة الكينو، فإن سحبتين متتاليتين سينتج عنهما ٢٠ كرة مشتركة في المتوسط.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

لنفترض أن c يمثل عدد الكراسي المُصنّعة في الساعة، وt يمثل عدد الطاولات. ستكون إيرادات الساعة 10×c + 20×t.

تنتج المناشير العشرة 600 دقيقة من النشر في الساعة. علمنا أن الكرسي يستغرق 10 دقائق من النشر، والطاولة 5 دقائق. لذا، يحد هذا من إنتاج الساعة إلى:

(1) 10c + 5t <= 600

تنتج المخرطات الستة 360 دقيقة من الخراطة في الساعة. علمنا أن الكرسي يستغرق 5 دقائق من المنشار، والطاولة 5 دقائق. لذا، يحد هذا من إنتاج الساعة إلى:

(2) 5ج + 5ت <= 360

تنتج آلات الصنفرة الثمانية عشر 1080 دقيقة صنفرة في الساعة. علمنا أن الكرسي يستغرق 5 دقائق من وقت المنشار، والطاولة 20 دقيقة. لذا، يحد هذا من إنتاج الساعة إلى:

(3) 5 ج + 20 ت <= 1080

يوضح الرسم البياني التالي القيود الثلاثة التي تفرضها مجموعات الآلات الثلاثة. يمكن للمصنع إنتاج أي مجموعة من الكراسي والطاولات ضمن خطوط الإنتاج الثلاثة. السؤال هو: أي خطوط الإنتاج الثلاثة تحقق أعلى إيرادات؟

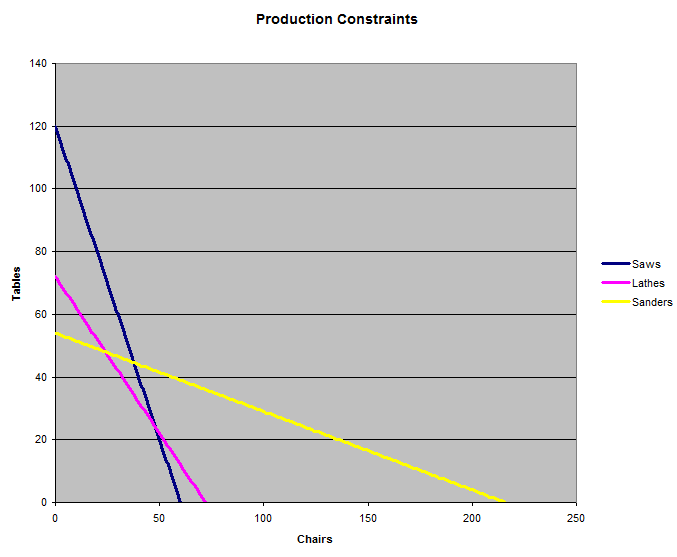
من المنطقي أن تكون الإجابة تقاطع خطين، أو صنع جميع الكراسي، أو صنع جميع الطاولات. لنحدد إذًا نقطة تقاطع الخطين. أولًا، لنحدد نقطة تقاطع المعادلتين (1) و(2). يمكننا تغيير تعبير <= إلى = فقط، لاستخدام الآلات بأقصى إمكاناتها.

(1) 10c + 5t = 600
(2) 5ج + 5ت = 360

اطرح (2) من (1):

5 ج = 240
ج = 48

إدخال 48 لـ c في المعادلة (1):

10×48 + 5t = 600
5t = 120
ت = 24

لذا، تلتقي المعادلتان (1) و(2) عند 48 كرسيًا و24 طاولة.

بعد ذلك، دعنا نجد مكان التقاء المعادلتين (2) و(3):

(2) 5ج + 5ت = 360
(3) 5 ج + 20 ت = 1080

طرح (2) من (3):

15 طن = 720
ت = 48

بوضع ذلك في (2) أو (3) يمكننا حل c، وهو 24.

وبالتالي، تلتقي المعادلتان (2) و(3) عند 24 كرسيًا و48 طاولة.

لا نحتاج إلى عناء البحث عن مكان التقاء المعادلتين (1) و(3)، لأننا نستطيع أن نرى من الرسم البياني أن مكان التقاء خطوط المنشار والصنفرة يقع خارج قيد المخرطة.

من الممكن أيضًا أن يكون صنع الكراسي فقط هو الإجابة الصحيحة. يوضح الرسم البياني أن المناشير هي أكبر عائق أمام صنع الكراسي فقط. من المعادلة (1)، إذا وضعنا 0 لعدد الطاولات، نحصل على c=60.

هناك احتمال آخر وهو صنع الطاولات فقط. يوضح الرسم البياني أن آلات الصنفرة ستشكل أكبر عائق. بإضافة صفر كراسي في المعادلة (3)، نجد أنه لا يمكن صنع أكثر من 54 طاولة.

يوضح الرسم البياني التالي إجمالي الإيرادات لكل إجابة ممكنة. تذكر أن الإيرادات هي ١٠ دولارات للكرسي و٢٠ دولارًا للطاولة.

إجمالي الإيرادات بالساعة

الكراسي	الجداول	ربح
0	54	1,080 دولارًا
24	48	1200 دولار
48	24	960 دولارًا
60	0	600 دولار

إذًا، أقصى ربح ممكن هو ١٢٠٠ دولار أمريكي من صنع ٢٤ كرسيًا و٤٨ طاولة. مع العلم أن هذا سيُبقي بعض المناشير غير مستخدمة لبعض الوقت. طُرح هذا السؤال ونوقش أيضًا في منتدى موقعي المرافق MathProblems.info ، المسألة رقم ٢٨.