اسأل الساحر #307
سأشارك في مسابقة "الميت بول" لعام ٢٠١٨. إليكم القواعد:
- يجب على كل لاعب تقديم قائمة تتضمن عشرة مشاهير أحياء تقل أعمارهم عن 100 عام.
- إذا مات أي من المشاهير، كما أشارت وكالة أسوشيتد برس في عام 2018، فإن أي شخص يحمل اسم المشاهير في قائمته سيحصل على 100 نقطة، حيث x هو العمر عند الوفاة.
- يفوز اللاعب الذي لديه أكبر عدد من النقاط في 1/1/2019.
انطلاقا من المتوسطات، ما هي الاستراتيجية المثلى لهذه اللعبة؟
بصفتك خبيرًا إكتواريًا سابقًا، فقد سألتَ الشخص المناسب. آمل ألا تعتبر جمعية الخبراء الإكتواريين إجابتي إساءةً للمهنة. مع ذلك، وللإجابة على سؤالك، استشرتُ جدول عمر الفترة لعام ٢٠١٤ من مكان عملي السابق، مكتب كبير الخبراء الإكتواريين في إدارة الضمان الاجتماعي.
يوضح جدول حياة الفترة، من بين أمور أخرى، احتمال الوفاة لشخص في أي عمر وجنس معينين في عام 2014. وباستخدام هذه المعلومات، قمت بإنشاء الجدول التالي، الذي يوضح احتمال الوفاة والنقاط المتوقعة لجميع الأعمار من 0 إلى 100 وكلا الجنسين.
جدول الحياة للفترة 2014 - مجموعة الوفيات
| عمر | احتمالية الموت - ذكر | احتمالية الموت - أنثى | مُتوقع النقاط — ذكر | مُتوقع النقاط — أنثى |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 13 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 25 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 26 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 27 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 28 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 29 | 0.001454 | 0.000648 | 0.103234 | 0.046036 |
| 30 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 32 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 34 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 35 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 36 | 0.001781 | 0.001008 | 0.113970 | 0.064538 |
| 37 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 38 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 39 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 42 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 44 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 47 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 48 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
يوضح الجدول أن الحد الأقصى للنقاط المتوقعة لرجل يبلغ من العمر 90 عامًا هو 1.645220.
تم طرح هذا السؤال ومناقشته في منتدياتي غير المخصصة للمقامرة، Diversity Tomorrow .
سجلتُ ٧٤٥٦ دورة في الروليت. النتائج كالتالي. أظن أن العجلة متحيزة، لكنني لست متأكدًا من أن البيانات كافية للعب.
بيانات الروليت
| الفوز رقم | الحوادث |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| المجموع | 7456 |
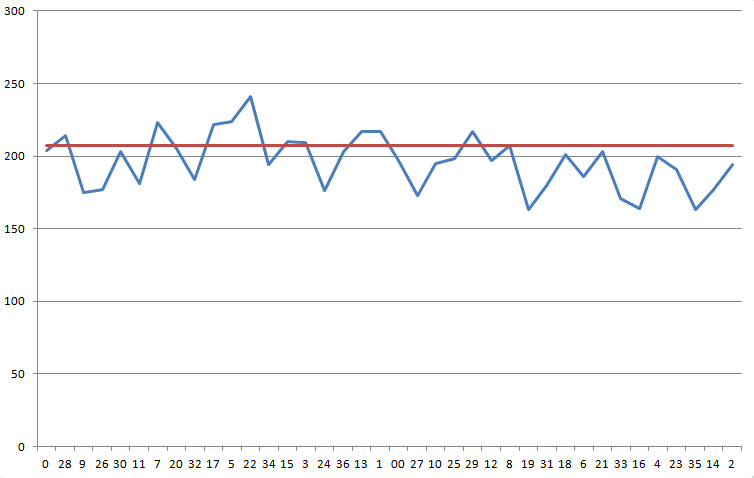
يوضح الرسم البياني التالي نتائجك بالترتيب على العجلة. يُظهر الخط الأزرق نتائجك. أما الخط الأحمر، فهو الرقم المطلوب، 207.11، لتجاوز نسبة 5.26% من هامش الكازينو.
يُعطي اختبار مربع كاي لهذا التوزيع قيمة إحصائية قدرها 68.1 مع 37 درجة حرية. احتمالية الحصول على نتيجة منحرفة بهذا الشكل أو أكثر هي 1 من 725.
لا أعتقد أن مربع كاي هو الاختبار الأمثل لهذه الحالة لأنه لا يأخذ في الاعتبار ترتيب النتائج، ولكن لا أعرف اختبارًا أفضل. اقترح البعض اختبار كولموغوروف-سميرنوف ، لكنني لا أعتقد أنه مناسب. إذا كانت هناك أي اختبارات أخرى مناسبة، فأنا أستمع إليها باهتمام.
أعتقد أنه لو راهنتَ على قوس الأرقام الثلاثة حول الرقم 5، لحققتَ ربحًا بنسبة 10.57% على عدد الدورات التي سجلتها. أما إذا زدتَ هذا الربح إلى قوس من 7 أرقام، فإن الفارق ينخفض إلى 2.84%.
إذا اضطررتُ للإجابة بلغة بسيطة وواضحة، فسأقول إن العجلة تُظهر دليلاً، وليس دليلاً قاطعاً، على تحيزها. مع ذلك، قد لا يكون هذا التحيز كافياً للتغلب على هامش الكازينو بشكل كبير وواثق. بافتراض أن الكازينو لا يُغيّر العجلات بين الطاولات، أرى أنه ينبغي جمع المزيد من البيانات قبل المراهنة بمبالغ كبيرة. مع الأسف، هذه الإجابة غير مُلزمة.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لاعبان، سام ودان، لكل منهما خمس عملات. يجب على كل منهما اختيار وضع من عملة إلى خمس عملات في يده. وفي الوقت نفسه، يجب على كل منهما الكشف عن عدد العملات التي لعبها. إذا اختار كلاهما نفس العدد، يفوز سام بجمع جميع العملات التي لعبها. إذا اختار كلاهما أعدادًا مختلفة، يجمع دان جميع العملات التي لعبها. بافتراض أن كلا اللاعبين منطقيان بارعان، ما هي الاستراتيجية الأمثل لدان؟
ينبغي على دان أن يجعل استراتيجيته عشوائية على النحو التالي:
- احتمال اختيار عملة واحدة = 77/548.
- احتمال اختيار عملة واحدة = 107/548.
- احتمال اختيار عملة واحدة = 117/548.
- احتمال اختيار عملة واحدة = 122/548.
- احتمال اختيار عملة واحدة = 125/548.
باستخدام هذه الاستراتيجية، يمكن لدان أن يتوقع الفوز بـ3.640510949 عملة في كل دور، بغض النظر عن عدد العملات التي يختارها سام.
يمكن العثور على الحل في موقع مشاكل الرياضيات الخاص بي، المشكلة رقم 230.
يمكنك العثور على سؤال ذي صلة، والذي أدى إلى هذا السؤال، في المنتدى الخاص بي في Wizard of Vegas .
تُلعب لعبة بلاك جاك "هوت أكشن بلاك جاك" في كازينو كاليفورنيا جراند بسان فرانسيسكو. قواعد اللعبة هي كما يلي:
- ستة مجموعات من الأوراق في لعبة خلط مستمرة مع 18 ورقة جوكر إضافية بقيمة اسمية 2.
- الموزع يضرب 17 ناعمة.
- مضاعفة على أي بطاقتين الأولى.
- إعادة تقسيم ما يصل إلى أربعة أيدي.
- لا يجوز سحب أو إعادة تقسيم الآسات.
- لا للاستسلام.
- تدفع لعبة البلاك جاك 6 إلى 5.
- إذا كانت البطاقتان الأوليتان للاعب عبارة عن جوكر، فإنه يحصل على مكافأة 4 إلى 1.
- إذا كانت البطاقتان الأوليتان للاعب من نوع الآسات، فإنه يحصل على مكافأة 5 إلى 1.
- يجب على اللاعب دفع عمولة بنسبة 5٪ للعب.
ما هي الاستراتيجية الأساسية وحافة المنزل؟
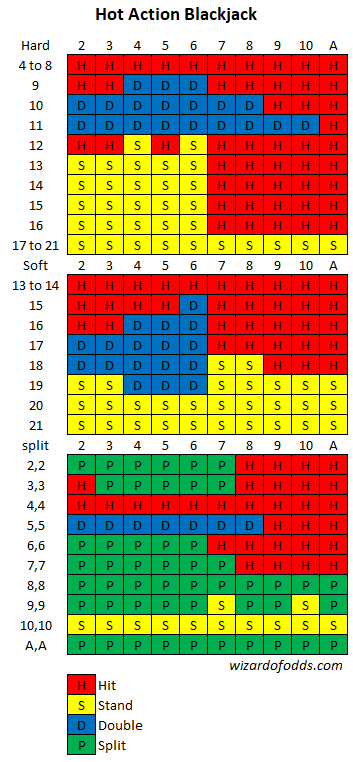
أولاً، إليكم استراتيجيتي الأساسية وفقًا لهذه القواعد:
بالنظر إلى كل شيء، أُظهر هامش ربح للكازينو بنسبة 6.01% (يا للأسف!) بناءً على الرهان الأولي. بمعنى آخر، إذا راهن اللاعب بمبلغ 100 دولار، دون احتساب عمولة الـ 5 دولارات، فمن المتوقع أن يخسر 6.01 دولار. وهذا يُوضح سبب تجنبي ألعاب الإيداع الخاصة باللاعبين في كاليفورنيا، إلا إذا كنتَ أنت من يقوم بالإيداع.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .