اسأل الساحر #322
جلستُ في لعبة تكساس هولدم، وكانت أعلى يد خلال الجولة هي ستريت فلش. علق لاعبان آخران على الطاولة بأنها ثالث فلش متتالي. ما احتمالات ذلك؟
في لعبة تكساس هولدم لعشرة لاعبين، بافتراض عدم انسحاب أي لاعب، فإن احتمال أن تكون اليد العليا ستريت أو رويال فلش هو ١ من ٣٥٠.١٤. واحتمال حدوث ذلك في ثلاث أيادٍ من أصل ثلاث هو ١ من ٤٢,٩٢٦,٤٩١.
مع ذلك، ربما كانت هذه الطاولة تعمل لساعات. ربما يكون السؤال الأكثر واقعية هو: ما احتمال حدوث ذلك مرة واحدة على الأقل في اليوم؟ بافتراض لعب لمدة ٢٤ ساعة كاملة و٢٤ يدًا في الساعة، ستكون الإجابة ١ من ٥٩٦٢١.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
بافتراض اتباع استراتيجية صحيحة، ما هو احتمال الفوز في لعبة Ultimate Texas Hold 'Em مع زيادة قدرها 4 أضعاف؟ لقد سجلت 96 يدًا بـ 4 أضعاف. وباستثناء الدفعات، حققت 66 فوزًا و30 خسارة. كيف يُقارن ذلك بالتوقعات؟
بافتراض استراتيجية رفع 4x الصحيحة، هناك احتمال لكل نتيجة، مع الأخذ في الاعتبار رفع 4x:
- الفوز: 58.82%
- الخسارة: 38.47%
- التعادل: 2.72%
إذا استبعدنا التعادلات، فإن احتمال الفوز هو 60.46%. في 96 جولة، العدد المتوقع للفوز بأربعة أضعاف هو 58.04. لذا، فإن 66 فوزًا يفوق التوقعات، ولكن ليس بشكل كبير.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لدى كلٍّ من أكسل وبوب مجموعة أوراقه الخاصة المكونة من 52 ورقة. يخلطانها عشوائيًا. ثم يقلبان ورقةً واحدةً في كل مرة، في آنٍ واحد، من كل مجموعة. ما احتمال أن يقلبا الورقة نفسها في نفس الوقت مرةً واحدةً على الأقل؟
من السهل تقدير الإجابة كالتالي: ١-(٥١/٥٢) ٥٢ = ٠٫٦٣٥٦٨٦٤٨. مع ذلك، فإن التقديرات غير مُرضية عقليًا. لذا، دعونا نجد حلًا دقيقًا!
الخطوة ١: للبدء، احسب عدد طرق ترتيب المجموعة الثانية من البطاقات عندما تكون البطاقة الأولى رقم ١. الإجابة هي عدد طرق ترتيب البطاقات الـ ٥١ الأخرى، أي ٥١! = ١٥٥١١١٨٧٥٣٢٨٧٣٨٢٢٨٠٢٢٤٢٤٣٠١٦٤٦٩٣٠٣٢١١٠٦٣٢٥٩٧٢٠٠١٦٩٨٦١١٢٠٠٠٠٠٠٠٠٠٠٠.
يمكن لأي بطاقة أن تتطابق مع المجموعة الأولى، لذا يجب علينا تطبيق هذا على جميع البطاقات الـ 52. هذا يعطينا 52 × 51! = 52! مجموعة تتطابق فيها بطاقة واحدة على الأقل.
الخطوة ٢: مع ذلك، في الخطوة ١، نحسب مرتين كل حالة تتطابق فيها بطاقتان. على سبيل المثال، إذا كانت البطاقتان الأوليتان ١ و٢، فسنحسب ٥٠ طريقة لترتيب البطاقات الأخرى مرتين، مرة للبطاقة ١ كالبطاقة الأولى، ومرة ثانية للبطاقة ٢ كالبطاقة الثانية. عدد طرق اختيار بطاقتين من أصل ٥٢ هو combin(٥٢،٢) = ١٣٢٦. لكل مجموعة من بطاقتين، هناك ٥٠ طريقة لترتيب البطاقات الأخرى. لذلك، في الخطوة ٢، نحتاج إلى طرح combin(٥٢،٢)*٥٠! = (٥٢*٥١/٢!)*٥٠! = ٥٢!/٢! مجموعة.
الخطوة 3: لنفترض أن أول ثلاث بطاقات في المجموعة العشوائية هي 1، 2، و3 بالترتيب. هناك 49 طريقة لترتيب البطاقات الـ 49 الأخرى. كنا سنعدّها ثلاث مرات في الخطوة الأولى لاختيار بطاقة مطابقة واحدة على الأقل. ثم سنطرح جميع طرق الجمع (combin(3,2)=3 لاختيار بطاقتين من هذه البطاقات الثلاث في الخطوة الثانية. لذا، في هذه الحالة، كان سيتم عدّها 3-3=0، لذا نحتاج إلى إضافتها مرة أخرى. هناك حالات مثل الجمع (combin(52,3) لاختيار 3 بطاقات مطابقة على الأقل. لذا نحتاج إلى إضافة الجمع (combin(52,3)*49! = 52*51*50*49!/3! = 52!/3!).
الخطوة 4: بعد ذلك، ضع في اعتبارك الحالة التي تكون فيها البطاقات الأربع الأولى في المجموعة العشوائية هي 1 و2 و3 و4 بالترتيب. يوجد 48 طريقة لترتيب البطاقات الـ 48 الأخرى. كنا سنحسبها أربع مرات في الخطوة الأولى للعد بحثًا عن بطاقة مطابقة واحدة على الأقل. ثم كنا سنطرح جميع الطرق combin(4,2)=6 لاختيار بطاقتين من هذه البطاقات الأربع في الخطوة 2. ثم كنا سنضيف جميع الطرق combin(4,3)=4 لاختيار 3 بطاقات من هذه البطاقات الأربع. إذن لدينا 4-6 + 4 = طريقتان لعد كل حالة من هذه الحالات. لذا نحتاج إلى طرح إحدى هذه الطرق، بحيث يتم حساب كل حالة مرة واحدة. يوجد combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! مثل هذه الحالات التي يجب إضافتها مرة أخرى.
سنستمر في القيام بذلك، بالتناوب بين الجمع والطرح لتصحيح العد المزدوج.
في النهاية، عدد الحالات التي تتطابق فيها بطاقة واحدة على الأقل من المجموعة العشوائية مع المجموعة المرتبة = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
هناك 52! = y = 5271776154963652194226185415451226599692124538619822080000000000000 إجمالي الطرق لطلب 52 بطاقة.
وبالتالي، فإن الإجابة هي x/y = 0.6321205588285576784044762298
احتمال عدم وجود تطابقات هو 1-(x/y) = 0.3678794411714423215955237702.
إذا كان هذا الرقم يبدو مألوفًا، فيجب أن يكون كذلك. 1/e = 0.3678794411714423215955237702.
لذا، يمكن تقدير الإجابة بشكل وثيق للغاية على أنها 1-(1/e).
الشكر والتقدير
تم إجراء الحسابات الرياضية في Pari/GP
لقد تم طرح هذه المشكلة ومناقشتها في المنتدى الخاص بي في Wizard of Vegas .
في المستند الذي يحمل عنوان احتمالات نمط البنغو (PDF) على موقعك، تشير إلى العدد المتوقع للمكالمات للعثور على الفائز، بافتراض وجود 300 بطاقة في اللعب، على النحو التالي:
- أربع زوايا: 8.43
- ماسة صغيرة: 11.833
كلا النمطين يتطلب أربع علامات فقط، ولهما طريقة واحدة للفوز. لماذا يختلف عدد الكرات المتوقع للفوز؟
هذا إجابة يصعب شرحها. دعوني أبدأ بالقول إن عدد مرات الرفض المتوقعة في لعبة بطاقة واحدة سيكون متساويًا. ومع ذلك، هناك تأثير ارتباط مع أكثر من بطاقة واحدة.
من الصعب إعطاء إجابة سريعة على هذا السؤال، ولكن إذا كان ذلك مُجبرًا، فذلك لأن نمط الزوايا الأربع يتطلب تركيزًا للكرات في عمودي B وO. من المرجح أن يُصاب نمط الماس الصغير بتوزيع أكثر تسطحًا للكرات على أعمدة B وN وO.
لنبسط اللعبة بحيث يكون فيها عدد لا نهائي من البطاقات، وتُسحب الكرات مع استبدالها. إليك عدد الكرات المطلوبة للفوز في كلتا اللعبتين:
- الزوايا الأربع: 2.5+2.5+((1/2)*10+(1/2)*(2.5+5)) = 13.75
- الماس الصغير: =(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
وهذا يوضح أن الزوايا الأربع تحتاج إلى 1.53 كرة إضافية.
من خلال تشغيل هذا من خلال محاكاة وفقًا لقواعد البنغو العادية، بافتراض وجود عدد لا نهائي من البطاقات، إليك النتائج:
- أربع زوايا: 12.8289
- الماس: 11.3645
هذه المرة مختلفة عن الكرات 1.46.
ما آمل أن أوضحه هو أن الأنماط تكون أكثر عرضة للتغطية بشكل أسرع إذا كانت العلامات موزعة على أعمدة أكثر. لهذا السبب، أعتقد أنه في لعبة بنغو واحدة، عادةً ما يكون البنغو الفائز أفقيًا.
تم طرح هذا السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .
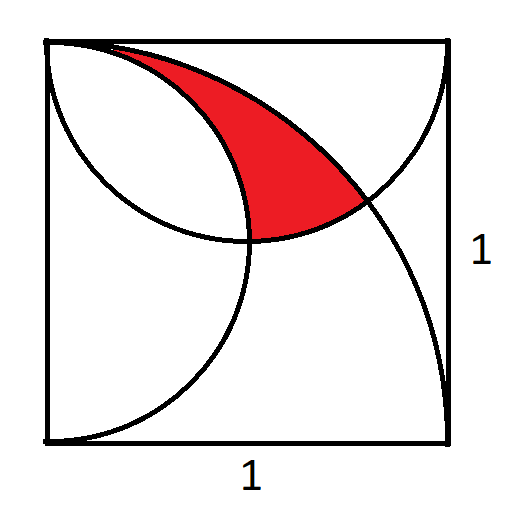
في الشكل أعلاه، يوجد ربع دائرة ونصفا دائرتان في مربع طول ضلعه واحد. السؤال: ما مساحة المنطقة الحمراء؟
انقر على الزر التالي للحصول على إجابتي.
انقر على الزر التالي للحصول على حلي.
هذا رابط لحلي . (PDF)
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
الشكر والتقدير: أود أن أشكر Mind Your Decisions على هذا اللغز الرياضي.


