اسأل الساحر #323
هل هذه البطاقة البارلاي جيدة؟

في الخطوة الأولى، عليك المراهنة ضد فارق النقاط في مباراة دوري كرة القدم الأمريكية (NFL). في وقت طرح هذا السؤال (2 يناير 2020)، كان فريق الفايكنج أقل حظًا بفارق 7.5 نقطة. وفقًا لحاسبتي لفارق النقاط البديلة في دوري كرة القدم الأمريكية (NFL) ، فإن احتمال فوز الفايكنج (+8.5) هو 52.22%.
في جميع الألعاب الأخرى، نظرتُ إلى خطوط الربح، وطرحتُ منها العصير، لمعرفة احتمالية الفوز. مع ذلك، يُظهر الجدول التالي احتمالية فوز كل جولة.
بطاقة ويليام هيل بارلاي
| رجل | النبيذ العادل | احتمال الفوز |
|---|---|---|
| القديسين -8.5 | -7.5 | 47.78% |
| الفايكنج +8.5 | 8.5 | 52.22% |
| هو | -135 | 57.45% |
| الفواتير | 135 | 42.55% |
| الوطنيون | -205 | 67.21% |
| جبابرة | 205 | 32.79% |
| بحر | -118 | 54.13% |
| فيل | 118 | 45.87% |
| جامعة ولاية لويزيانا | -200 | 66.67% |
| كليمسون | 200 | 33.33% |
| نادي كرة القدم الأسترالي | -130 | 56.52% |
| تقنية الاتصال قريب المدى | 130 | 43.48% |
الاختياران اللذان يتمتعان بأفضل فرصة للفوز في الخطوة الأولى هما باتريوتس وجامعة ولاية لويزيانا. إليكم احتمالية فوز اختياراتي الموصى بها:
- الفايكنج +8.5 — 52.22%
- الباتريوتس — 67.21%
- جامعة ولاية لويزيانا — 66.67%
حاصل ضرب هذه الاحتمالات هو ٢٣.٤٠٪. الحصول على ٤ مقابل ١ ينتج عنه عائد ٤ × ٢٣.٤٠٪ = ٩٣.٦٠٪. بمعنى آخر، نسبة ربح الكازينو هي ٦.٤٠٪. لذا، أنصحك بترك هذا الأمر كما هو.
أفكر في إنشاء رهان جانبي لإصدارات البلاك جاك "ادفع 22"، والذي سيدفع 11 إلى 1 إذا خسر الموزع بـ 22. ما هي احتمالات ذلك؟
أفكر في إنشاء رهان جانبي لإصدارات البلاك جاك "ادفع ٢٢"، والذي سيفوز إذا خسر الموزع بـ ٢٢. ما هي احتمالات الربح، وما هي ميزة الكازينو؟
بافتراض أن الموزع يسحب يده دائمًا (حتى لو كان كل اللاعبين قد خسروا بالفعل)، فإنني أظهر احتمال الخسارة على 22 بنسبة 7.88% إذا كان الموزع يقف على 17 ناعمة و8.00% إذا حصل على 17 ناعمة.
بافتراض أن الموزع حصل على 17 ناعمة، ففي حالة فوز 11 إلى 1، ستكون نسبة ربح الكازينو 4.04%. أما في حالة فوز 10 إلى 1، فترتفع إلى 12.04%.
يجب أن أحذرك وأنصح اللاعبين بأن هذا سيكون قابلاً للعد (اصمت يا ويز!).
لدى آمي وبوب مسابقة للفوز بأربع رميات لعملة عادلة. ترغب آمي في المراهنة بمبلغ 8000 دولار على نفسها للفوز بالمسابقة. مع ذلك، يُسمح لها بالمراهنة مرة واحدة فقط في كل مرة. جميع الرهانات تدفع مبلغًا متساويًا. كيف يمكنها تنظيم رهاناتها بحيث تربح 8000 دولار إذا فازت بالسلسلة بأكملها وتخسر 8000 دولار إذا فاز بوب؟
انقر على الزر أدناه للحصول على الإجابة.
هناك ١٦ حالة محتملة في منتصف السلسلة. يوضح الجدول التالي الرهان الذي يجب على إيمي وضعه في كل حالة ورصيدها قبل الرهان باتباع هذه الاستراتيجية.
إجابة
| إيمي | بوب | توازن | رهان |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | عام 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | عام 2000 |
| 2 | 0 | 5000 | عام 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | عام 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
انقر على الزر أدناه للحصول على الحل.
يترك:
- أ = إيمي تفوز
- ب = بوب يفوز
- w = صافي فوز إيمي حتى الآن في السلسلة
- f(a,b,w) = حجم رهان إيمي في المباراة التالية
في مثل هذه الألغاز، من الأفضل عادةً البدء من النهاية ثم الانطلاق نحو البداية. مع ذلك، من السهل ملاحظة ما يلي:
f(3,3,0) = 8,000
في هذه الحالة، تُعتبر اللعبة السابعة "الفائز يأخذ كل شيء". يجب أن يكون ربح إيمي صفرًا، وأن تراهن بـ 8000 في آخر رمية، مما يمنحها ربحًا قدره 8000 إذا فازت في الرمية، وخسارة قدرها 8000 في حال عدم فوزها.
بالعودة خطوةً إلى الوراء، ماذا لو فازت هي بثلاثة وبوب باثنين؟ إذا فازت في الرمية التالية، فستفوز باللعبة بأكملها. إذا خسرت، ستكون نتيجتها 3-3. بناءً على f(3,3,0)، يجب أن يكون لديها 0 إذا كانت النتيجة 3,3. لذا، نحتاج أن يكون لديها 8000 إذا فازت في الرمية التالية و0 بخلاف ذلك. ما سيصل إليه هذا هو ربح صافٍ في منتصف 4000 ورهان بنفس المبلغ. إذًا:
ف(3، 2، 4000) = 4000
بالعودة خطوة أخرى، ماذا لو فازت هي بثلاثة وبوب مرة واحدة؟ إذا فازت في الجولة التالية، فستفوز باللعبة بأكملها. إذا خسرت، ستكون نتيجتها 3-2. بناءً على f(3,2,4000)، يجب أن يكون لديها 4000 إذا كانت النتيجة 3,2. لذا، نحتاج أن يكون لديها 8000 إذا فازت في الجولة التالية و4000 بخلاف ذلك. ما سنحصل عليه هنا هو ربح صافٍ في المنتصف [(4000 + 8000) / 2 = 6000] ورهان بنصف المسافة بين هذين الهدفين، [(8000-4000) / 2 = 2000]. إذن:
f(3,1,6000) = 2,000
بالعودة خطوة أخرى، ماذا لو فازت بثلاثة وبوب بلا أي فوز؟ إذا فازت في الجولة التالية، فستفوز باللعبة بأكملها. إذا خسرت، ستكون نتيجتها 3-1. بناءً على f(3,1,6000)، يجب أن يكون لديها 6,000 إذا كانت النتيجة 3,1. لذا، نحتاج أن يكون لديها 8,000 إذا فازت في الجولة التالية و6,000 بخلاف ذلك. ما سنحصل عليه هنا هو ربح صافٍ في المنتصف [(6,000 + 8,000) / 2 = 7,000] ورهان بنصف المسافة بين هذين الهدفين، [(8000-4000) / 2 = 2000]. إذن:
f(3,0,7000) = 1,000
من المأمول أن يكون فوز إيمي الصافي صفرًا في حال التعادل. في أي سيناريو تعادل، ستكون احتمالية فوزها بالسلسلة بأكملها 50%. مع وجود أهداف متوازنة للفوز/الخسارة 8000 في كلتا الحالتين، عليها المراهنة على صفر وإلا ستكون لديها فرصة عدم تحقيق أيٍّ من الهدفين النهائيين.
بعد ذلك، إذا تأخرت إيمي في السلسلة، فيجب أن يكون صافي ربحها -1 مضروبًا في صافي الربح لو كانت متقدمة بنفس النتيجة. على سبيل المثال، لنفترض أن إيمي ٢ - بوب ٣ (أو ٢-٣). إذا خسرت في الجولة التالية، فستخسر اللعبة بأكملها. إذا فازت، فستكون نتيجتها ٣-٣. بناءً على f(3,3,0)، يجب أن يكون ربحها ٠ إذا كانت النتيجة ٣,٣. لذا، نحتاج أن يكون ربحها ٠ إذا فازت في الجولة التالية، و-٨٠٠٠ بخلاف ذلك. ما سيصل إليه الربح هنا هو خسارة صافية في منتصف ٤٠٠٠ ورهان بنفس المبلغ. إذًا:
ف(2،3،-4000)=4000
وبنفس المنطق:
f(1,3,-6000) = 2,000
f(0,3,-7000) = 1,000
بعد ذلك، ما هو رهان آمي إذا كانت النتيجة ٢-٢؟ إذا فازت في الفليب، فستكون النتيجة ٣-٢. بناءً على ما سبق، نرى أنها بحاجة إلى فوز صافٍ قدره ٤٠٠٠ بهذه النتيجة. ونرى أيضًا أنه إذا كانت متأخرة ٢-٣، فيجب أن تكون خسارتها الصافية ٤٠٠٠. وبالتالي، عليها أن تراهن بمبلغ ٤٠٠٠:
f(2,2,0) = 4,000
بالعودة خطوةً إلى الوراء، ماذا لو كانت النتيجة ٢-١؟ لقد حددنا أنها بحاجة إلى صافي ربح ٦٠٠٠ إذا فازت في الجولة التالية (نتيجة ٣-١) وصافٍ ربح ٠ إذا خسرت (نتيجة ٢-٢). ما سيصل إلى هنا هو صافي ربح في المنتصف [(٦٠٠٠ + ٠) / ٢ = ٣٠٠٠] ورهان نصف المسافة بين هذين الهدفين، [(٦٠٠٠ - ٠) / ٢ = ٣٠٠٠]. إذًا:
f(2,1,3000) = 3000
بالعودة خطوةً أخرى من هنا، ماذا لو فازت مرتين ولم يربح بوب شيئًا؟ إذا فازت في الجولة التالية، ستكون النتيجة 3-0. إذا خسرت، ستكون النتيجة 2-1. يجب أن يكون صافي ربحها 7000 عند 3-0 و3000 عند 2-1. ما سيصل إليه الأمر من نتيجة 2-0 هو فوز صافٍ في المنتصف [(7000 + 3000) / 2 = 5000] ورهان بنصف المسافة بين هذين الهدفين، [(7000-3000) / 2 = 2000]. إذًا:
f(2,0,5000) = 2000
من خلال قلب تلك النتائج حيث حصلت أليس على فوزين وحصل بوب على عدد أقل، فإننا نعلم أيضًا:
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
كما شرحنا سابقًا، يجب أن يكون صافي فوز آمي صفرًا إذا كانت السلسلة متوازنة، لذا عند نتيجة 1-1، يجب أن يكون صافي فوزها صفرًا. عند نتيجة 2-1، يجب أن تكون متقدمة بمقدار 2000، وعند نتيجة 1-2، يجب أن تكون متأخرة بمقدار 2000. وبالتالي، عند نتيجة تعادل 1-1، يجب أن تراهن بمبلغ 2000، أو:
f(1,1,0) = 2,000
ماذا لو كانت آمي متقدمة بفارق ١-٠؟ لقد حددنا أنها بحاجة إلى التقدم بفارق ٥٠٠٠ نقطة عند ٢-٠. أما عند ١-١، فيجب أن تكون متعادلة.ما سيصل إليه الأمر من نتيجة ١-٠ هو فوز صافٍ في المنتصف [(٥٠٠٠ + ٠) / ٢ = ٢٥٠٠] ورهان نصف المسافة بين الهدفين، [(٥٠٠٠ - ٠) / ٢ = ٢٥٠٠]. إذًا:
f(1,0,2500) = 2,500
عن طريق قلب النتيجة إلى 0-1:
f(0,1,-2500) = 2,500
وأخيرًا، وصلنا إلى المباراة الأولى بنتيجة 0-0. نحتاج أن تكون آمي متقدمة بمقدار 2500 إذا فازت في الجولة التالية، وناقصة بمقدار 2500 إذا خسرت. لذا، رهان بقيمة 2500 سيوصلنا إلى هناك. أو:
f(0,0,0) = 2,500
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
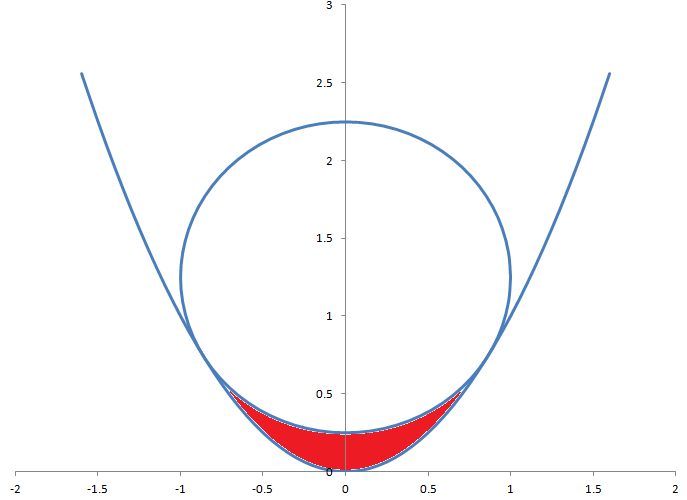
دائرة نصف قطرها ١ مماسة لقطع مكافئ معادلته ص = س ٢. ما مساحة المنطقة الحمراء بين الدائرة والقطع المكافئ؟
انقر على الزر أدناه للحصول على الإجابة.
هذا هو الحل الخاص بي. (PDF)
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لقد حصلت على هذه المشكلة من Presh Talwalker من Mind Your Decisions .


