WOO logo

يوصي المعالج

اسأل الساحر #326

ما هي استراتيجية الصليب الحديدي في لعبة الكرابس وما رأيك فيها؟

مجهول

الصليب الحديدي هو طريقة للمراهنة على الميدان ووضع الرهانات للفوز بأي رمية نرد باستثناء الرقم 7. يغطي الميدان بالفعل الأرقام 2 و3 و4 و9 و10 و11 و12. سيضيف اللاعب إلى هذا الرهان رهانات على الأرقام 5 و6 و8 لتغطية بقية الأرقام، بالإضافة إلى الرقم 7. يوضح الجدول التالي الحسابات الرياضية برهان ميداني بقيمة 5 دولارات، ورهان مركز بقيمة 5 دولارات على الرقم 5، ورهان مركز بقيمة 6 دولارات على الرقمين 6 و8.

الصليب الحديدي

مجموع النرد يفوز التركيبات احتمال يعود
2 10 1 0.027778 0.277778
3 5 2 0.055556 0.277778
4 5 3 0.083333 0.416667
5 2 4 0.111111 0.222222
6 2 5 0.138889 0.277778
7 -22 6 0.166667 -3.666667
8 2 5 0.138889 0.277778
9 5 4 0.111111 0.555556
10 5 3 0.083333 0.416667
11 5 2 0.055556 0.277778
12 15 1 0.027778 0.416667
36 1.000000 -0.250000

تُظهر الخلية السفلية اليمنى من الجدول خسارة متوقعة قدرها 0.25 دولار. يبلغ إجمالي مبلغ الرهان 22 دولارًا. هذا يجعل هامش الكازينو الإجمالي 0.25 دولار/22 دولارًا = 1/88 = 1.14%.

في هذه المرحلة، قد تتساءل كيف يمكن أن تكون هذه الميزة أقل من ميزة الكازينو لكل رهان على حدة. والجواب هو أن ميزة الكازينو البالغة 1.52% عند وضع 6 و8، و4.00% عند وضع 5، تعتمد على كل رهان مُحَلّ. إذا حُدِّدت ميزة الكازينو على رهانات الوضع على أساس كل لفة، فإن ميزة الكازينو عند وضع 6 أو 8 هي 0.46%، وعند وضع 5 هي 1.11%.

يمكننا الوصول إلى نسبة 1.14% للمنزل من خلال أخذ متوسط مرجح لجميع الرهانات التي تم إجراؤها، على النحو التالي:

(5 دولارات * 2.78% + 5 دولارات * 1.11% + 12 دولارات * 0.46%) / 22 = 0.25 دولار / 22 دولار = 1.14%.

احذر من الكازينوهات التي تدفع فقط ٢ إلى ١ لرهان ١٢ على أرض الملعب. أصرّ على الحصول على ٣ إلى ١ كاملةً. يُضاعف الدفع القصير هامش ربح الكازينو على هذا الرهان من ٢.٧٨٪ إلى ٥.٥٦٪.

برأيي، مقارنةً بمعظم الألعاب، يُعدّ رهان 1.14% رهانًا جيدًا. مع ذلك، يُمكنك تحقيق نتيجة أفضل بكثير في لعبة الكرابس. على سبيل المثال، مع احتمالات 3-4-5x، ورهانات "النجاح" و"النجاح الكامل"، يُمكنك خفض هامش الكازينو إلى 0.37%. أما في المقابل، أي المراهنة على "عدم النجاح" و"النجاح الكامل"، بالإضافة إلى وضع الرهانات الكاملة، فيُصبح هامش الكازينو 0.27%.

ما هو العدد المتوقع من رميات النرد العادل لتدوير كل وجه مرتين على الأقل؟

Ace2

الإجابة هي 390968681 / 16200000 = تقريبًا 24.13386919753086

[spoiler=الحل]

مع أنه يمكن حل هذه المشكلة باستخدام سلسلة ماركوف طويلة ومملة، إلا أنني أُفضّل الحل الشامل. أشرح كيفية استخدام هذه الطريقة في صفحاتي حول رهان النار ومكافآت الكرابس .

تخيل أنه بدلاً من تحديد الأحداث المهمة برمي النرد، واحدة تلو الأخرى، اعتبرها لحظة زمنية. افترض أن الوقت الفاصل بين الأحداث لا يعتمد على الذاكرة، حيث يبلغ متوسطه وحدة زمنية واحدة. بمعنى آخر، يتبع الوقت الفاصل بين الأحداث توزيعًا أُسيًا بمتوسط 1. لن يكون هذا مهمًا عند تقييم الرهان، لأن الأحداث لا تزال تقع واحدة تلو الأخرى.

وفقًا لتوزيع بواسون، فإن احتمالية رمي أي جانب من جوانب النرد صفر مرة في x وحدات زمنية هي exp(-x/6)*(x/6) 0/0 ! = exp(-x/6). ويقول بواسون أيضًا إن احتمالية رمي أي جانب مرة واحدة بالضبط هي exp(-x/6)*(x/6) 1/1 ! = exp(-x/6) * (x/6). وبالتالي فإن احتمالية رمي أي جانب مرتين أو أكثر في x وحدات زمنية هي 1 - exp(-x/6)*(1 + (x/6)). واحتمالية رمي جميع الجوانب الستة مرتين على الأقل هي (1 - exp(-x/6)*(1 + (x/6))) 6. واحتمالية عدم رمي جانب واحد على الأقل مرتين على الأقل تساوي:

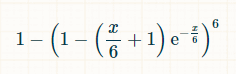
لف كل جانب مرتين

نحن بحاجة إلى دمج ذلك على مدار الوقت لمعرفة مقدار الوقت الذي سيمضي، في المتوسط، حيث لم يتم تحقيق الهدف المطلوب.

لحسن الحظ، يُمكننا استخدام حاسبة تكامل في هذه المرحلة. بالنسبة للحاسبة المُرفقة، ضع 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 في مربع النص التالي لـ "حساب تكامل"، وتحت "مخصص"، اضبط حد التكامل من 0 إلى ∞.

الإجابة هي 390968681 / 16200000 = تقريبًا 24.13386919753086

[/كابح]

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

لدي سؤال مكون من جزأين.

بالنسبة للجزء الأول، معطى:
  • x + y + z = 1
  • x^2 + y^2 + z^2 = 4
  • x^3 + y^3 + z^3 = 9

ما هو x^4 + y^4 + z^4 ؟

بالنسبة للجزء الثاني، ما هو الجواب للحالة العامة عندما:

  • x + y + z = أ
  • x^2 + y^2 + z^2 = b
  • x^3 + y^3 + z^3 = c

مجهول

[spoiler=الإجابات]

السؤال 1: 97/6 = تقريبًا 16.166666

السؤال 2: أ 4/6 + (4/3) أ ج - أ 2 ب + ب 2/2

[/كابح]

[spoiler=الحل]

لمشاهدة حلي (PDF)

[/كابح]

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

ابدأ بنرد ذي ستة أوجه عادلة، ثم رميته ست مرات، وسجل نتائج كل رمية. ثم اكتب هذه الأرقام على الوجوه الستة لنرد عادل آخر غير مُسمّى. على سبيل المثال، إذا كانت رمياتك الست هي 3، 5، 3، 6، 1، و2، فلن يكون على النرد الثاني الرقم 4؛ بل سيكون عليه رقمان 3.

بعد ذلك، تُلقي حجر النرد الثاني ست مرات. تأخذ هذه الأرقام الستة وتكتبها على وجوه حجر نرد عادل آخر، ثم تُكمل عملية توليد حجر نرد جديد من الحجر السابق.

في النهاية، ستحصل على نرد بنفس الرقم على جميع أوجهه الستة. ما هو متوسط عدد مرات الانتقال من نرد لآخر (أو إجمالي الرميات مقسومًا على 6) للوصول إلى هذه الحالة؟

rsactuary

تقريبًا 9.65599148388557

[spoiler=الحل]

لتجنب الالتباس، دعونا نُسمّي النرد الأولي بالأحرف بدلًا من الأرقام. دعونا نُسمّي كل حالة ممكنة للنرد بالأحرف. على سبيل المثال، AAABBC تعني ثلاثة من حرف واحد، واثنين من حرف آخر، وواحد من ثالث. الحالة الأولية ستكون ABCDEF.

ليكن E(ABCDEF) هو العدد المتوقع للرميات من الحالة ABCDEF.

E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656

بناءً على عدد تركيبات الانتقال من حالة إلى أخرى، تُظهر مصفوفة الانتقال التالية عدد الطرق للانتقال من كل حالة ابتدائية (العمود الأيسر) إلى كل حالة جديدة. استغرق بناء هذه المصفوفة بشكل صحيح بضع ساعات.

مصفوفة الانتقال أ

ولاية
قبل		 أأأأ أأأأب أأأأب أأأأأأ أأأبب AAABBC AABBCC أأأب ج د أأ ب ب ج د AABCDE أ ب ج د هـ
أأأأب 15,626 18,780 9,750 2500 - - - - - - -
أأأأب 4,160 13,056 19,200 10,240 - - - - - - -
أأأأأأ 1,458 8,748 21,870 14,580 - - - - - - -
أأأب سي 4,098 12,348 8,190 2,580 7,920 10,080 1,440 - - - -
AAABBC 794 5,172 8,670 5,020 6,480 17,280 3,240 - - - -
AABBCC 192 2,304 5,760 3,840 5,760 23,040 5,760 - - - -
أأأب ج د 732 4,464 4,140 1,680 7,920 14,400 2,520 4,320 6,480 - -
أأ ب ب ج د 130 1,596 3,150 1,940 5,280 16,800 3,600 4,800 9,360 - -
AABCDE 68 888 1,380 760 3,960 11,520 2,520 7,200 14,040 4,320 -
أ ب ج د هـ 6 180 450 300 1800 7,200 1800 7,200 16,200 10,800 720

لن أدخل في محاضرة طويلة عن جبر المصفوفات، باستثناء أن نقول أن المصفوفة B هي كما يلي:

المصفوفة ب

ولاية
قبل		 أأأأب أأأأب أأأأأأ أأأب سي AAABBC AABBCC أأأب ج د أأ ب ب ج د AABCDE أ ب ج د هـ
أأأأب -27876 9750 2500 0 0 0 0 0 0 -46656
أأأأب 13056 -27456 10240 0 0 0 0 0 0 -46656
أأأأأأ 8748 21870 -32076 0 0 0 0 0 0 -46656
أأأب سي 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
AAABBC 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
AABBCC 2304 5760 3840 5760 23040 -40896 0 0 0 -46656
أأأب ج د 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
أأ ب ب ج د 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
AABCDE 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
أ ب ج د هـ 180 450 300 1800 7200 1800 7200 16200 10800 -46656

الجواب هو محدد المصفوفة B لمحدد المصفوفة A:

تحديد (أ) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000

تحديد (ب) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000,000

تحديد (ب) / تحديد (أ) = تقريبًا 9.65599148388557

[/كابح]