اسأل الساحر #335
قرأتُ عن لعبة "الملكي العكسي" ذات العائد ١٠٥.٢٢٪ في مقالتكم على موقع "ساحر فيغاس". تفترض هذه العائدات استراتيجيةً مثالية، بما في ذلك ترتيب البطاقات. ما هو العائد إذا افترضتُ فوزًا متوسطًا في "الملكي"؟ ماذا لو استخدمتُ استراتيجية "بوكر المكافآت ٦-٥" الاعتيادية، وهي جدول الدفع الأساسي؟
بافتراض عدم وجود أي انحرافات في الاستراتيجية، ستكون واحدة من كل 60 جائزة ملكية متتالية. تبلغ قيمة الجائزة الكبرى للجائزة الملكية القابلة للعكس 161,556 لكل رهان. أي جائزة ملكية أخرى تبلغ قيمتها 800 لكل رهان. وبالتالي، يكون متوسط ربح الجائزة الملكية (1/60) × 161,556 + (59/60) × 800 + 17,396 لكل رهان.
إذا افترضنا أن جميع أفراد العائلة المالكة يدفعون 17,396 ويلعبون الإستراتيجية المثلى بناءً على فوز هذا الفرد الملكي، فإن العائد ينخفض إلى 103.56%.
إذا لعبنا استراتيجية 6-5 Bonus Poker القياسية، وهي جدول الدفع الأساسي، فإن العائد ينخفض إلى 101.97%.
افترض أن مربع الوحدة له إحداثيات (0,0)، (1,0)، (1,1)، (0,1). يمتد الخط أ من (0,0) إلى (1,1). يمتد الخط ب من (1,0) إلى 0.5,1. ما نصف قطر الدائرة المماسّة للخطين أ، ب، وأسفل الدائرة؟
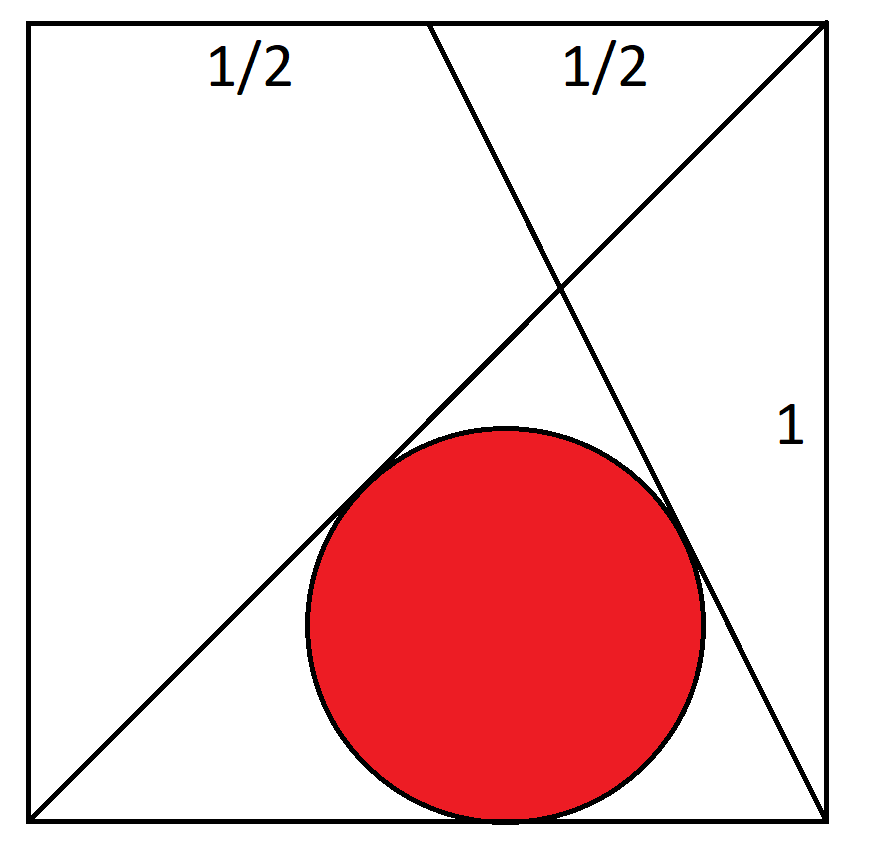
ظهر هذا اللغز في طبعة أكتوبر 2020 من نشرة مينسا.
وهنا الحل الخاص بي (PDF).
تم طرح هذه المشكلة ومناقشتها في المنتدى الخاص بي في Wizard of Vegas .
ما هو احتمال الحصول على Yahtzee إذا كانت هذه هي الفئة الوحيدة المتبقية لديك على البطاقة؟
للقراء غير الملمين بلعبة ياتزي، السؤال هو: ما احتمال الحصول على خمسة من نفس النوع في ثلاث رميات لخمسة نرد؟ بعد كل رمية، عليك اختيار النرد الذي ستحتفظ به والنرد الذي ستُعيد رميه.
فيما يلي النتائج المحتملة بعد اللفة الأولى أو أي لفة يقوم فيها اللاعب برمي 4 أو 5 أحجار نرد.
- خمسة من نفس النوع = 6*(1/6)^5 = 0.000772
- أربعة من نفس النوع = (1/6)^3*(5/6)*4 = 0.015432
- ثلاثة من نفس النوع = (1/6)^2*(5/6)^2*COMBIN(4,2) = 0.115741
- اثنان من نفس النوع = 4*(1/6)*(5/6)^3 = 0.385802
- واحد من نوعه = 6*5!/6^5 = 0.092593
وهنا الاحتمالات بعد الاحتفاظ بالزوج.
- خمسة من نفس النوع =(1/6)^3 = 0.004630
- أربعة من نفس النوع = 3*(1/6)^2*(5/6) = 0.069444
- ثلاثة من نفس النوع = 3*(1/6)*(5/6)^2+5*(1/6)^3 = 0.370370
- اثنان من نفس النوع = (5/6)^3-5*(1/6)^3 = 0.555555
فيما يلي الاحتمالات بعد الحصول على ثلاثة من نوع واحد:
- خمسة من نفس النوع =(1/6)^3 = 0.002778
- أربعة من نفس النوع = 2*(1/6)*(5/6) = 0.27778
- ثلاثة من نفس النوع = (5/6)^2 = 0.694444
فيما يلي الاحتمالات بعد الحصول على أربعة من نوع واحد:
- خمسة من نفس النوع = 1/6 = 0.166667
- أربعة من نفس النوع = 5/6 = 0.83333
مع احتمالات التقدم تلك، إليك احتمالات كل حالة بعد اللفة الثانية:
- خمسة من نفس النوع = 0.000772 + 0.015432*0.166667 + 0.115741*0.002778 + 0.385802*0.004630 + 0.092593* 0.000772 = 0.012631
- أربعة من نفس النوع = 0.015432*0.166667 + 0.115741*0.27778 + 0.115741*0.27778 = 0.116970
- ثلاثة من نفس النوع = 0.115741*0.694444 + 0.385802*0.370370 + 0.092593*0.115741 = 0.409022
- اثنان من نفس النوع = 0.385802*0.555555 + 0.092593*0.385802 = 0.450103
- فريدة من نوعها = 0.092593 * 0.092593 = 0.008573
باستخدام نفس احتمالات التقدم، إليك احتمال ظهور Yahtzee بعد اللفة الثالثة:
خمسة من نفس النوع = 0.012631 + 0.116970*(1/6) + 0.409022*(1/6)^2 + 0.450103*(1/6)^3 + 0.008573*(1/6)^4 = 0.046029.
بالنسبة لأولئك الذين يفضلون جبر المصفوفة، هناك مصفوفة الانتقال:
| 0.092593 | 0.694444 | 0.192901 | 0.019290 | 0.000772 |
| 0.000000 | 0.555556 | 0.370370 | 0.069444 | 0.004630 |
| 0.000000 | 0.000000 | 0.694444 | 0.277778 | 0.027778 |
| 0.000000 | 0.000000 | 0.000000 | 0.833333 | 0.166667 |
| 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
إذا كانت المصفوفة أعلاه هي M، فإن الحالة بعد ثلاث رميات ستكون M 3 ، على النحو التالي:
| 0.000794 | 0.256011 | 0.452402 | 0.244765 | 0.046029 |
| 0.000000 | 0.171468 | 0.435814 | 0.316144 | 0.076575 |
| 0.000000 | 0.000000 | 0.334898 | 0.487611 | 0.177491 |
| 0.000000 | 0.000000 | 0.000000 | 0.578704 | 0.421296 |
| 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
يمكن العثور على احتمالية الحصول على Yahtzee بعد ثلاث لفات في الخلية الموجودة في الزاوية اليمنى العليا.
بعد مشاهدة برنامج "مناورة الملكة" ، لاحظتُ أن جميع مبارياته لم تنتهِ بالتعادل. كنتُ أعتقد أن مباريات الشطرنج في المستويات العليا تشهد الكثير من التعادل. بالنسبة لمستوى الأستاذ الكبير، ما نسبة المباريات التي تنتهي بالتعادل؟
وفقًا لمقال "هل ازداد عدد التعادلات في الشطرنج؟" على موقع ChessBase.com، ذكر الكاتب تشيو تشو أنه في 78,468 مباراة مُصنّفة بين لاعبين بتقييم 2600 نقطة أو أكثر (يتطلب الأمر 2500 نقطة ليصبح المرء أستاذًا كبيرًا)، كانت النتائج التالية:
- فوز الأسود: 18.0%
- يفوز الأبيض: 28.9%
- التعادل: 53.1%


