اسأل الساحر #336

هذه لعبة رائعة للاعب! موقعهم الإلكتروني لا يُفصّل التفاصيل، لذا سأفترض أنها للبطاقتين الأوليين فقط. رأيتُها في نشرة بلاك جاك الحالية القديمة من أكتوبر ٢٠١٨، ومعظم الطاولات لها القواعد التالية:

• الموزع يضرب 17 ناعمة
• ستة طوابق
• تدفع لعبة البلاك جاك 3 إلى 2
• مسموح بالمضاعفة بعد الانقسام
• يُسمح بإعادة تقسيم الآسات

تقول حاسبة حافة المنزل في لعبة البلاك جاك الخاصة بي أن هذه القواعد لها حافة منزل بنسبة 0.55% مع الخلط المستمر و 0.57% مع بطاقة مقطوعة.

بغض النظر عن القواعد، فإن احتمال الحصول على 16 دولارًا في أول ورقتين هو 6.51%. الحصول على 16 دولارًا بنسبة 6.51% يساوي 1.04 دولارًا لكل يد. سأفترض أن الحد الأدنى للرهان هو 25 دولارًا لأن معظم الكازينوهات ترفع الحد الأدنى للرهان في ظل جائحة كورونا. باستثناء المكافأة، تبلغ الخسارة المتوقعة لكل يد 0.14 دولارًا عند رهان 25 دولارًا. هذا يجعل الربح المتوقع لكل يد 1.04 دولارًا - 0.14 دولارًا = 0.90 دولارًا. نسبةً إلى مبلغ الرهان، تبلغ هذه النسبة 3.59%!

إذا افترضنا حالة جيدة للعب ثلاث جولات بقيمة 25 دولارًا بمعدل 80 جولة في الساعة، فسيكون من المتوقع أن يكون الفوز في كل ساعة 216 دولارًا!

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

[spoiler=الحل]

أولاً، هناك combin(25,3) = 2,300 تركيبة ممكنة للأوتاد.

كم من هذه التركيبات تُشكّل مثلثًا؟ لنستخدم هذه اللوحة لمساعدتك:

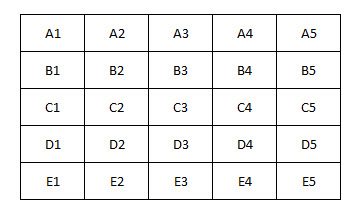
أولاً، هناك خمسة صفوف وخمسة أعمدة وقطران. لكل منها، هناك 10 طرق لوضع الأوتاد في خط واحد. إذن، لدينا 12 × 10 = 120 طريقة.

ثانيًا، هناك أربع طرق لربط المربع المركزي لصف/عمود بمربع مركزي لصف/عمود مجاور. بعبارة أخرى، هذه هي المواضع الثلاثة:

• أ3، ب4، ج5
• C5، D4، E3
• هـ3، د2، ج1
• ج1، ب2، أ3

إذن، نحن الآن عند 120 + 4 = 124

ثالثًا، هناك أربعة خطوط قطرية مختلفة تمثل أربع مسافات:

• أ2، ب3، ج4، د5
• ب5، ج4، د3، هـ2
• هـ4، د3، ج2، ب1
• د1، ج2، ب3، أ4

لكلٍّ منها، هناك 4 طرق لوضع ثلاثة أوتاد. هذا يعني أن 4 × 4 = 16.

نحن الآن عند 124+16 = 140

رابعًا، لننظر إلى طريقة حركة الأحصنة في الشطرنج، على شكل حرف L 2×1. لكل زاوية طريقتان لحركة الحصان. في كل منهما، يمكن للحصان أن يتحرك مجددًا على نفس الخط الذي شكله في الحركة الأولى. إذن، 4×2 = 8 إضافية:

• أ1، ج2، هـ3 أ1، ب3، ج5
• أ5، ب3، ج1
• أ5، ج4، هـ3
• E5، C4، A3
• هـ5، د3، ج1
• هـ1، د3، ج5
• هـ1، ج2، أ3

هناك أيضًا أربعة خطوط فارس تمر عبر المركز:

• أ2، ج3، هـ4
• A4، C3، E2
• ب5، ج3، د1
• د5، ج3، ب1

بإضافة خطوط الفرسان الـ 12، نحصل على 140 + 12 = 152

إذا كان هناك 2300 تركيبة إجمالية و152 خطًا شكليًا، فإن 2300 - 152 = 2148 لا تشكل خطوطًا وبالتالي تشكل مثلثات.

وبالتالي، فإن إجابتنا هي 2,148/2,300 = 93.39%.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

لتبسيط الأمر، لنفترض أن إعادة تقسيم الآسات غير مسموح بها. تذكر أيضًا أن لعبة ٢١ الإسبانية تستخدم مجموعات إسبانية من ٤٨ بطاقة، بدون ١٠. وأخيرًا، تذكر أن ٢١ نقطة تُعتبر فائزًا تلقائيًا في لعبة ٢١ الإسبانية.

حتى بدون هذه القاعدة، يجب على اللاعب دائمًا تقسيم الآسات. احتمال الحصول على زوج من الآسات في لعبة إسبانية بأربعة أوراق هو combin(16,2)/combin(192,2) = 120/18336 = 0.65%.

احتمال حصول كل آص على ١٠ هو (٤ × ١٢) / (٤٨ × ١٢ - ٢) = ٤٨ / ١٩٠ = ٢٥٫٢٦٪. مع وجود آصين، العدد المتوقع الذي سيتحول إلى بلاك جاك هو ٢ × ٤٨ / ١٩٠ = ٩٦ / ١٩٠ = ٠٫٥٠٥٣.

كل بلاك جاك يساوي نصف وحدة إضافية. وبالتالي، فإن قيمة هذه القاعدة هي (١٢٠/١٨٣٣٦)*(٩٦/١٩٠)*(١/٢) = ٠٫١٧٪.

حتى مع هذه القاعدة، لا ينبغي للاعب تقسيم العشرات، لذا لا داعي للقلق بشأن ذلك. لذا، تُخفّض هذه القاعدة هامش الكازينو بنسبة 0.17%.

[spoiler=الحل]

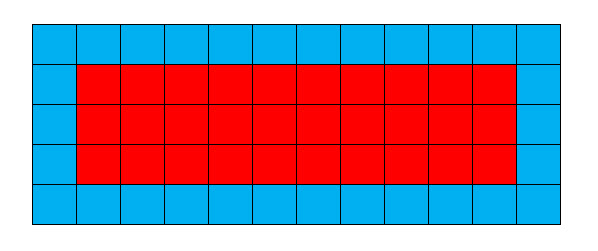
لنفترض أن x و y هما أبعاد المستطيل الداخلي.

مساحة هذا المستطيل هي x*y.

مساحة المحيط هي 2س + 2ص + 4

يُعطى أن xy = 2x+2y+4

xy-2x = 2y + 4

x(y-2) = 2y+4

x=(2y+4)/(y-2)

يجب أن يكون y أكبر من أو يساوي 3. دعنا نرى ما هو x لبعض قيم y التي تساوي أو أكبر من 3.

إذا كان y = 3، فإن x = 10
إذا كان y = 4، فإن x = 6
إذا كان y = 5، فإن x = 14/3
إذا كان y = 6، فإن x = 4

إذًا، ٣×١٠ و٤×٦ هما الحل. أما ٦×٤ فليس كذلك، لأنه ليس حلاً وحيدًا. كلما كبرت قيمة ص، صغرت قيمة س. وكما يجب أن تكون قيمة ص مساوية أو أكبر من ٣، كذلك يجب أن تكون قيمة س. هناك قيمة واحدة أخرى ممكنة لقيمة س، حيث إنها تتناقص مع ارتفاع قيمة ص، وهي س=٣. ومع ذلك، إذا كانت س=٣، فإن ص=١٠، وهي أيضًا ليست حلاً وحيدًا.

إذن، الإجابة هي ٢: ٣×١٠ و٤×٦ للمستطيل الداخلي. إذا كنت تفضل حساب الحلول حسب المستطيل الخارجي، فسيكون ٥×١٢ و٦×٨.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .