يوصي المعالج
-
$مكافأة ترحيبية بقيمة 11000 -
مكافأة ترحيبية 100% -
$مكافأة ترحيبية بقيمة 3000
اسأل الساحر #338
ما هو متوسط عدد اللفات اللازمة باستخدام نردين لتحقيق مجموع من 2 إلى 12؟
[spoiler=الحل]
يمكن استخدام سلسلة ماركوف للإجابة على هذا السؤال، لكنني أُفضّل التفاضل والتكامل. يكمن السر في أن تكون الإجابة واحدة إذا كان الزمن بين الرميات موزعًا أسيًا بمتوسط يساوي واحدًا. مع ذلك، يمكن التعبير عن الإجابة بالتكامل من صفر إلى ما لا نهاية لما يلي:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))
يمكنك حل مثل هذه التكاملات بسهولة باستخدام حاسبة التكامل .
يمكنك أيضًا حل أي مشكلة من هذا القبيل باستخدام حاسبة التجارب المتوقعة الخاصة بي.
[/كابح]هناك نملة في منتصف مربع. تبعد ١٧ بوصة عن الزاوية العلوية اليسرى، و٢٠ بوصة عن الزاوية العلوية اليمنى، و١٣ بوصة عن الزاوية السفلية اليمنى.
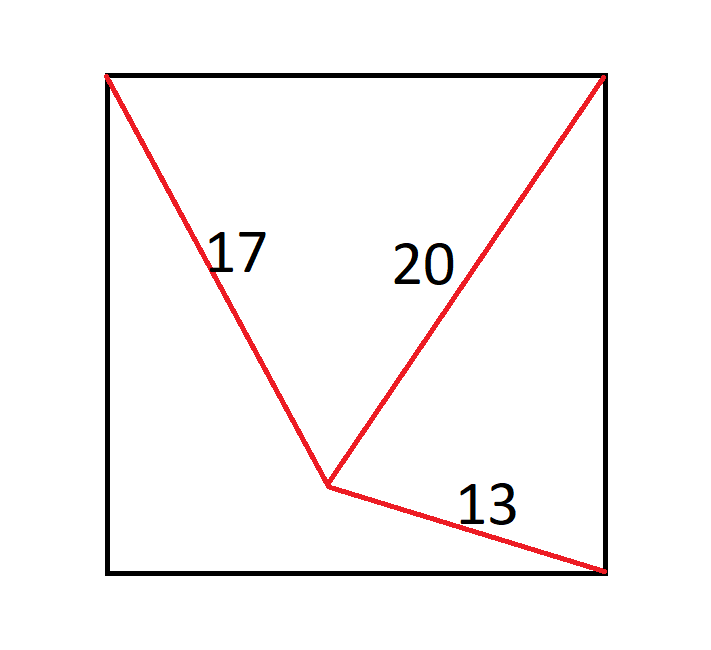
ما هو حجم المربع؟
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
[spoiler=إجابة]369 بوصة مربعة.
[spoiler=الحل]
أولاً، قم بتدوير المثلث ABE بمقدار 90 درجة لتشكيل مثلث جديد BDF.
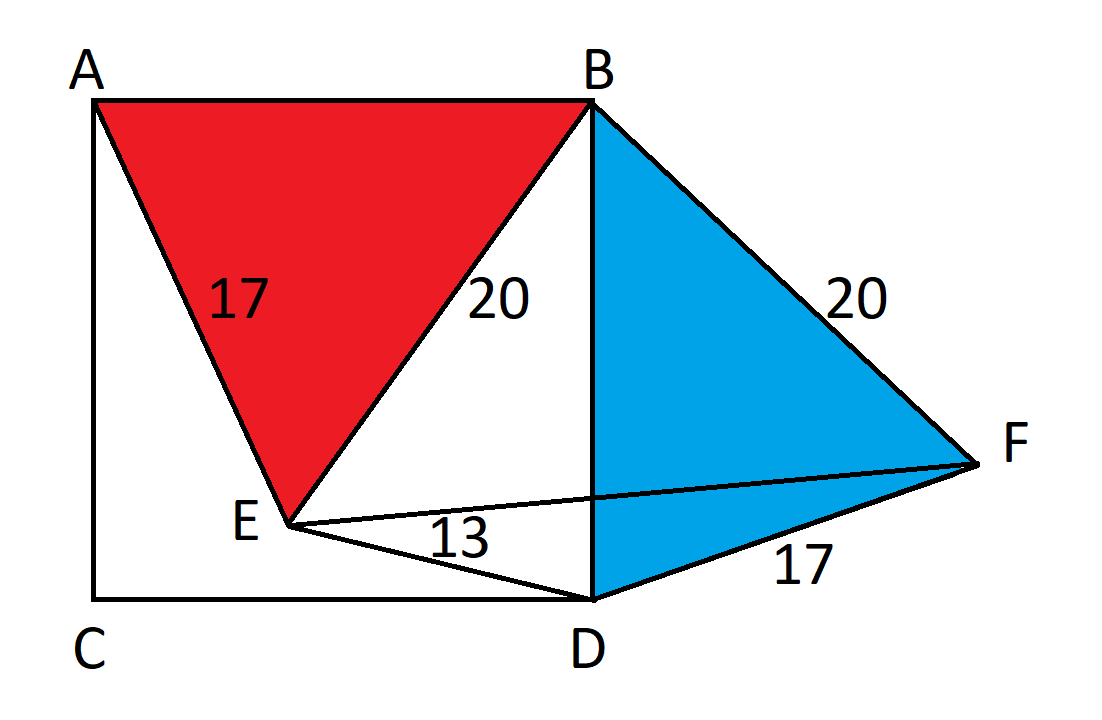
بما أن المثلث مُدار بزاوية ٩٠ درجة، فإن الزاوية EBF = ٩٠، حسب التعريف. ووفقًا لصيغة فيثاغورس، EF = ٢٠ × الجذر التربيعي (٢).
بموجب قانون جيب التمام: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*الجذر التربيعي(2)*جيب التمام(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
تذكر، sin^2(x) + cos^2(x) = 1. دعنا نستخدم ذلك لحل sin(DEF).
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
بعد ذلك، ضع في اعتبارك زاوية BED.
زاوية BED = زاوية BEF + زاوية FED.
نعلم أن الزاوية EBF تساوي 90 درجة، وهي مثلث متساوي الساقين. هذا يجعل الزاوية EBF تساوي 45 درجة.
وبالتالي، زاوية BED = 45 درجة + زاوية FED.
تذكر، cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
دعونا نطبق قانون جيب التمام مرة أخرى، هذه المرة على المثلث BED.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD هو ضلع المربع المعني، لذا BD^2 هي مساحة هذا المربع، والتي أظهرنا أنها 369.
[/كابح]تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لعبة "دروب ديد" تُلعب بخمسة أحجار نرد قياسية. تبدأ دورك برمي جميع الأحجار الخمسة. إذا لم يكن أي منها 2 أو 5، تجمع مجموع الأحجار، وتضيفه إلى مجموع نقاطك، ثم ترميه مرة أخرى. إذا رميت أي أحجار نرد تحمل الرقم 2 أو 5، تكون نتيجتك صفرًا. تُعلن جميع الأحجار التي تحمل الرقم 2 أو 5 ميتة وتُستبعد. ثم ترميها مرة أخرى بالنرد المتبقي. يستمر اللعب إما بتسجيل نقاط أو إزالة الأحجار. ينتهي دورك بإخراج جميع الأحجار، وعندها يُقال إنك ميت. تُجمع جميع رمياتك للحصول على نتيجتك النهائية. أعلى نتيجة تفوز.
ما هي نتيجتك المتوقعة لهذه المباراة؟
[spoiler=الحل]
لنبدأ بالسيناريو الذي يتبقى فيه نرد واحد ونتحرك للخلف.
دع المتغير a يكون النقاط الإضافية المتوقعة مع بقاء نرد واحد.
المتوسط الذي لا يساوي 2 أو 5 هو (1+3+4+6)/4 = 7/2.
أ = (2/3)×(أ + 7/2).
أ/3 = 7/3.
أ = 7.
الآن، دعنا نحسب b، النقاط المتوقعة مع وجود نردين متبقيين.
ب = (2/3) 2 ×(ب + 2 × (7/2)) + 2×(2/3)×(1/3)×أ.
ب = 11.2.
الآن، دعنا نحسب c، النقاط المتوقعة مع وجود ثلاثة أحجار نرد متبقية.
ج = (2/3) 3 ×(ج + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×ب + 3×(2/3)×(1/3) 2 ×ب.
ج = 1302/95 = 13.705263.
الآن، دعنا نحسب d، النقاط المتوقعة مع وجود أربعة أحجار نرد متبقية.
د = (2/3) 4 ×(د + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×ج + 6×(2/3) 2 ×(1/3) 2 ×ب + 4×(2/3)×(1/3) 3 ×أ.
د = 3752/247 = 15.190283.
أخيرًا، دعنا نحسب e، النقاط المتوقعة مع وجود خمسة نرد متبقية.
ه = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×أ.
هـ = 16.064662.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
[/كابح]لنأخذ رهان Pairplus في بوكر الثلاث أوراق، والذي يتبع جدول الدفع 1-4-6-30-40. مع ذلك، يدفع هذا الرهان جائزة كبرى لبطاقة رويال صغيرة من البستوني، و25% من تلك الجائزة لبطاقة رويال صغيرة من الأنواع الثلاثة الأخرى. ما هو ارتفاع العداد المطلوب ليكون الرهان عادلاً؟
الجواب هو 384 مرة مبلغ الرهان.
لكل 100 رهان إضافي فوق ذلك، يرتفع العائد بنسبة 0.79%.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .