اسأل الساحر #352
ما هو مقدار الزيادة التي تحدثها المدفوعات القصوى في حافة المنزل في Mississippi Stud؟
سؤال جيد. يجب على لاعبي Mississippi Stud أن يدركوا أن الحد الأقصى للدفعات قد يقلل من أرباحهم في لعبة Royal Flush، مما يزيد من هامش ربح الكازينو.
أعلى عائد في بطولة ميسيسيبي ستاد هو 500 إلى 1 لـ "رويال فلاش"، وينطبق على جميع الرهانات. لدى اللاعب فرصتان لرفع رهانه الأولي حتى 3 أضعاف، لذا يمكن أن يصل رهانه النهائي إلى 7 أضعاف رهانه الأولي. إذا كان اللاعب يأمل في "رويال"، فعليه رفع الحد الأقصى للرهانات.
أقصى مبلغ يمكن للاعب المراهنة به على الرهان الأولي في بطولة ميسيسيبي ستاد، دون التأثر بسقف السداد، هو الحد الأقصى للدفع/3500. على سبيل المثال، إذا كان الحد الأقصى للدفع 80,000 دولار، فإن أقصى مبلغ أنصح به للمراهنة على الرهان الأولي هو 22.86 دولار. وأود تقريب هذا المبلغ إلى 20 دولارًا.
يوضح الجدول التالي هامش ربح الكازينو في مختلف الرهانات ومتوسط الأرباح القصوى. يفترض الجدول استراتيجية مثالية للاعب دون حد أقصى للأرباح. لاحظ كيف يزداد هامش ربح الكازينو مع زيادة حجم الرهان وانخفاض الحد الأقصى.
ميزة المنزل مع حد الدفع
| رهان | الحد الأقصى 50,000 دولار | الحد الأقصى 80,000 دولار | الحد الأقصى 100,000 دولار |
|---|---|---|---|
| 15 دولارًا | 5.02% | 4.91% | 4.91% |
| 20 دولارًا | 5.15% | 4.91% | 4.91% |
| 25 دولارًا | 5.22% | 5.04% | 4.91% |
| 50 دولارًا | 5.38% | 5.28% | 5.22% |
| 75 دولارًا | 5.49% | 5.37% | 5.33% |
| 100 دولار | 5.64% | 5.41% | 5.38% |
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
وجّهت شركة فيتال فيغاس انتقاداتٍ للاعبٍ بسبب إكراميته بمبلغ ٢٠٠ دولار فقط في جائزةٍ كبرى بقيمة ١.١ مليون دولار. ما هي قواعد الإكرامية في مثل هذه الحالة؟
نعم، في حين أنهم يوبخون اللاعب على الإكرامية الصغيرة، فإنهم يتهربون بسهولة من السؤال حول ما ينبغي أن تكون الإكرامية المناسبة.
ليس فقط أن آداب الإكراميات غير واضحة للجوائز الكبرى، بل حتى للجوائز الصغيرة. تتباين الآراء حولها، وكثير منها من أشخاص لم يسبق لهم الفوز بجائزة كبرى.
أولاً، دعوني أؤكد أن الإكرامية ليست اختيارية. من المتوقع أن تُدفع في الكازينو مقابل الخدمة التي تتلقاها، وذلك حسب المبلغ الذي ربحته ومستوى الخدمة. من السهل أن يصبح المرء مغروراً في هذه المرحلة، ويُبرر لنفسه عدم دفع إكرامية. صحيح أن الإكرامية نظام معيب، ولكنه النظام الذي نتبعه. إذا لم توافق ورفضت الإكرامية، فلا تطلب أي خدمة يُتوقع منك دفع إكرامية مقابلها.
ثانيًا، بعد تحديد قيمة الجائزة الكبرى، ما هو المبلغ الذي يجب على اللاعب دفعه كإكرامية؟ سأقتصر هذا النقاش على الحالات التي يفوز فيها اللاعب بجائزة كبرى واحدة فقط. تختلف القواعد إذا فاز اللاعب بالعديد منها، وهو أمر طبيعي عند مستويات الرهان العالية جدًا. تذكر أن قواعد مراجعة أوراق الجائزة الكبرى هي:
- الفوز بمبلغ 1200 دولار أو أكثر في "الفتحات".
- الفوز بمبلغ 1500 دولار أو أكثر في لعبة الكينو.
- الفوز بمبلغ 5000 دولار أو أكثر في بطولة البوكر.
- الفوز بمبلغ 600 دولار أو أكثر و300 ضعف الرهان على الأقل في ألعاب الطاولة.
ما أنصح به من إكراميات؟ سبق أن قلتُ إن الإكرامية تتراوح بين ٠.٥٪ و٢٪ من قيمة الجائزة الكبرى، وكلما زادت قيمة الجائزة الكبرى، انخفضت النسبة المئوية. مع ذلك، لم أكن أفكر في جوائز كبرى بهذا الحجم آنذاك. أعتقد أن هذا النطاق مناسب حتى ١٠٠,٠٠٠ دولار أمريكي تقريبًا.
دفعني هذا السؤال إلى ابتكار صيغة محددة، أعتقد أنها مناسبة لأي جائزة كبرى تتراوح قيمتها بين ١٢٠٠ دولار وملايين الدولارات. ها هي:
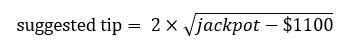
إذا لم تتمكن من رؤية الصورة، فهي 2×sqrt(الجائزة الكبرى - 1100 دولار).
فيما يلي ما تعطيه الصيغة لبعض مبالغ الجائزة الكبرى الشائعة.
جدول النصائح المقترحة
| الفوز بالجائزة الكبرى | نصيحة |
|---|---|
| 1200 دولار | 20 دولارًا |
| 2000 دولار | 60 دولارًا |
| 5000 دولار | 125 دولارًا |
| 10,000 دولار | 189 دولارًا |
| 20,000 دولار | 275 دولارًا |
| 50,000 دولار | 442 دولارًا |
| 100,000 دولار | 629 دولارًا |
| مليون دولار | 1,999 دولارًا |
في حالة مبلغ ١٫١ مليون دولار، تقترح صيغتي أن يكون المبلغ ٢٠٩٦٫٥٧ دولارًا. أعتقد أنه من المناسب تقريب المبلغ إلى ٢٠٠٠ دولار. بالطبع، يجب مراعاة عوامل أخرى أيضًا، مثل جودة الخدمة.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لأي عدد كبير مُعطى، ما هو متوسط المسافة بين الأعداد الأولية القريبة منه؟ وكم عدد الأعداد الأولية الأصغر منه؟
تقدير جيد جدًا لمتوسط المسافة بين الأعداد الأولية بالقرب من أي عدد كبير n هو ln(n). ومن اللافت للنظر مدى جودة هذا التقدير.
كدليل على ذلك، يوضح الجدول التالي نطاق أول 15 مليون عدد أولي، في مجموعات من مليون عدد. يوضح الجدول متوسط المسافة بين الأعداد الأولية وتقدير متوسط المسافة. التقدير هو اللوغاريتم الطبيعي لمتوسط أكبر وأصغر عدد أولي في النطاق. على سبيل المثال، للمجموعة الخامسة عشرة من مليون عدد أولي، يكون ln((256,203,221+275,604,541)/2).
متوسط المسافة بين الأعداد الأولية
| أول رئيس في النطاق | آخر رئيس في النطاق | الأعداد الأولية في النطاق | متوسط المسافة | تقدير | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | مليون | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | مليون | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | مليون | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | مليون | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | مليون | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | مليون | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | مليون | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | مليون | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | مليون | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | مليون | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | مليون | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | مليون | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | مليون | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | مليون | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | مليون | 19.40132 | 19.39864545 |
المصدر: الفجوات بين الأعداد الأولية في صفحات الأعداد الأولية.
للحصول على عدد الأعداد الأولية تحت أي عدد معطى، نبدأ بدمج تقدير متوسط المسافة لـ ln(n). سيعطينا هذا مجموع متوسط المسافات بين الأعداد الأولية حتى أي عدد n.
ما هو تكامل f(n)=ln(n)؟ تذكر أن التكامل بالتجزيء يُخبرنا:
تكامل f(n)*g'(n) dn = f(n)*g(n) - تكامل (f'(n)*g(n)) dn
ليكن f(n)=ln(n) وg'(n)=1. عندها، f'(n)=1/n وg(n)=n. تكامل ln(n) سيكون ln(n)*n - تكامل ((1/n)*n) = ln(n)*n - n = n*(ln(n)-1)
إذا قسمنا n*(ln(n)-1) على n، نحصل على متوسط المسافة بين الأعداد الأولية لمجموعة الأعداد من 2 إلى n. وهذا هو ln(n)-1.
إذا قسمنا n على هذه المسافة المتوسطة بين الأعداد الأولية، نحصل على متوسط عدد الأعداد الأولية تحت n، والذي يساوي n/(ln(n)-1).
كدليل، يُظهر الجدول التالي عدد الأعداد الأولية تحت أعداد كبيرة مختلفة والقيمة المُقدّرة. يُرجى المعذرة عن دقة الأرقام الخمسة عشر المعنوية، وهي أقصى ما يسمح به برنامج إكسل. رجاءً، يُمكن لأحدكم إنشاء جدول بيانات يستوعب المزيد.
متوسط المسافة بين الأعداد الأولية
| ن | الأعداد الأولية تحت n | ن/(لن(ن)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 100,000 | 9,592 | 9,512 |
| مليون | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 100,000,000 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 455,052,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
المصدر: كم عدد الأعداد الأولية الموجودة؟ في صفحات الأعداد الأولية.


