اسأل الساحر #353
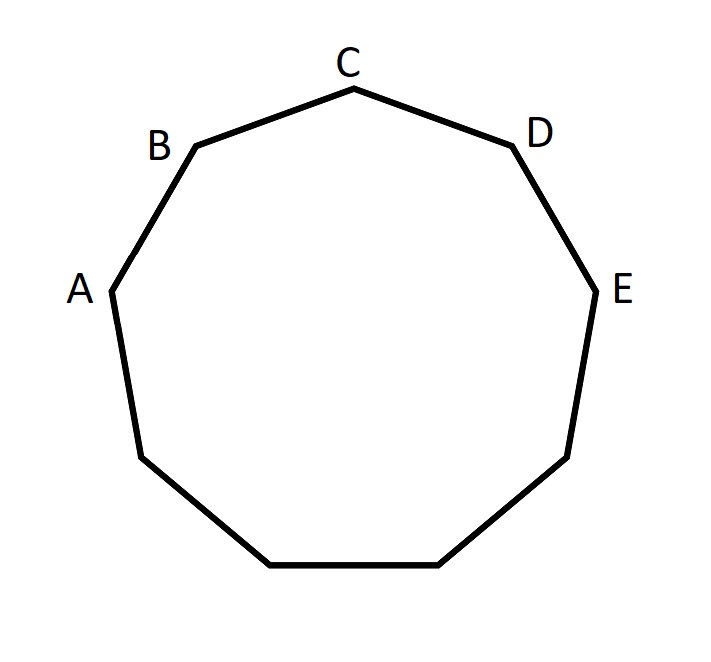
الشكل أعلاه هو شكل تسعي يبلغ طول ضلعه واحدًا.
أيهما أكثر، AB+AC أم AE؟
تم أخذ هذه المشكلة من إصدار مارس 2021 من نشرة مينسا.
وهنا الحل لهذه المشكلة. (PDF)
كيف يمكنني بسهولة العثور على الجذر التربيعي لأي عدد مكون من ثلاثة أو أربعة أرقام، على افتراض أن الإجابة عدد صحيح؟
يوضح الجدول التالي الأرقام من 0 إلى 9، ومربع كل رقم والرقم الأخير من هذا المربع.
الرقم الأخير من الأعداد المربعة
| إبداعي رقم | مربع | الرقم الأخير من المربع |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
لاحظ أن الأرقام هي مربعات زوجية تنتهي دائمًا بـ 0، 1، 4، 5، 6، أو 9. وهذا ينطبق على جميع المربعات، لأن الرقم الأخير من الرقم الأصلي يُحدد الرقم الأخير من المربع.
الخطوة ١: بناءً على الرقم الأخير من الجذر التربيعي، يمكننا استخدام الجدول التالي لتحديد الرقم الأخير من الجذر التربيعي. على سبيل المثال، إذا كان الرقم ٢٨٠٩ هو الرقم، فإن الرقم الأخير من الجذر التربيعي هو ٣ أو ٧.
الرقم الأخير من الرقم الأصلي
| الرقم الأخير من الجذر التربيعي | الرقم الأخير من المربع |
|---|---|
| 0 | 0 |
| 1 | 1 أو 9 |
| 4 | 2 أو 8 |
| 5 | 5 |
| 6 | 4 أو 6 |
| 9 | 3 أو 7 |
الخطوة الثانية: بعد ذلك، خذ الرقم الأصلي واحذف الرقمين الصحيحين. على سبيل المثال، إذا كان الرقم الأصلي ٢٨٠٩، فاستخدم ٢٨.
الخطوة ٣: أوجد أصغر عدد مربع أصغر من أو يساوي ناتج الخطوة ٢. ثم احسب الجذر التربيعي لهذا العدد. على سبيل المثال، أصغر عدد مربع أصغر من ٢٨ هو ٢٥. احسب الجذر التربيعي لـ ٢٥ لتحصل على ٥.
إذا لم تحفظ المربعات حتى الرقم 100، فيمكنك استخدام الجدول التالي.
الجزء الأول من الجذر التربيعي
| الخطوة 2 | الخطوة 3 |
|---|---|
| من 1 إلى 3 | 1 |
| من 4 إلى 8 | 2 |
| من 9 إلى 15 | 3 |
| من 16 إلى 24 | 4 |
| من 25 إلى 35 | 5 |
| من 36 إلى 48 | 6 |
| من 49 إلى 63 | 7 |
| من 64 إلى 80 | 8 |
| من 81 إلى 99 | 9 |
الخطوة 4: إذا كانت النتيجة من الخطوة 1 هي 0 أو 5، فضع ذلك بعد النتيجة من الخطوة 3 وقد انتهيت.
بخلاف ذلك، ليكن a = الناتج من الخطوة 3. ليكن b=a×(a+1). على سبيل المثال، إذا كانت النتيجة من الخطوة 3 هي 5، فإن b=5×6=30.
الخطوة 5: إذا كان b < a، فإن الرقم الأخير من الجذر التربيعي هو الأصغر من الاحتمالات من الخطوة 1. وإلا، إذا كان b >= a، فإنه يكون الأكبر من الاحتمالين.
الخطوة 6: للحصول على الجذر التربيعي، خذ النتيجة من الخطوة 3 ثم اتبعها بالنتيجة من الخطوة 5. بمعنى آخر 10 × (الخطوة 3) + الخطوة 5.
دعونا نلقي نظرة على بعض الأمثلة:
أوجد الجذر التربيعي لـ 256.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 4 أو 6.
- الخطوة 2: حذف الرقمين الأخيرين، نحصل على 2.
- الخطوة 3: أصغر مربع أقل من أو يساوي 2 هو 1. الجذر التربيعي لـ 1 هو 1.
- الخطوة 4: 1*(1+1) = 2.
- الخطوة 5: النتيجة من الخطوة 4 تساوي النتيجة في الخطوة 2، لذلك نستخدم الخيار الأكبر من الخطوة 1 كالرقم الأخير، وهو 6.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 1 و 6 = 16.
أوجد الجذر التربيعي لـ 1369.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 3 أو 7.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 13.
- الخطوة 3: أصغر مربع أقل من أو يساوي 13 هو 9. الجذر التربيعي لـ 9 هو 3.
- الخطوة 4: 3*(1+3) = 12.
- الخطوة 5: النتيجة من الخطوة 2 أكبر من تلك في الخطوة 4، لذلك نستخدم الخيار الأكبر من الخطوة 1 كالرقم الأخير، وهو 7.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 3 و 7 = 37.
أوجد الجذر التربيعي لـ 2704.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 2 أو 8.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 27.
- الخطوة 3: أصغر مربع أقل من أو يساوي 27 هو 25. الجذر التربيعي لـ 25 هو 5.
- الخطوة 4: 5*(1+5) = 60.
- الخطوة 5: النتيجة من الخطوة 2 أقل من النتيجة في الخطوة 4، لذلك نستخدم الخيار الأصغر من الخطوة 1 كالرقم الأخير، وهو 2.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 5 و 2 = 52.
أوجد الجذر التربيعي لـ 5625.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 5.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 56.
- الخطوة 3: أصغر مربع أقل من أو يساوي 56 هو 49. الجذر التربيعي لـ 49 هو 7.
- الخطوة 4: النتيجة من الخطوة 1 هي 0 أو 5، لذا فإن الإجابة هي النتيجة من الخطوة 3 المضافة إلى الخطوة 1: 7 و 5 = 75
أوجد الجذر التربيعي لـ 6561.
- الخطوة 1: الرقم الأخير هو 1 أو 9.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 65.
- الخطوة 3: أصغر مربع أقل من أو يساوي 65 هو 64. الجذر التربيعي لـ 64 هو 8.
- الخطوة 4: 8*(1+8) = 72.
- الخطوة 5: النتيجة من الخطوة 2 أقل من النتيجة في الخطوة 4، لذلك نستخدم الخيار الأقل من الخطوة 1 كالرقم الأخير، وهو 1.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 8 و 1 = 81.
يمكنك مشاهدة عرض توضيحي لهذه الطريقة على اليوتيوب .
خلال 12 ساعة من لعب البلاك جاك، ما هو احتمال رؤية 60 فوزًا أو أكثر على التوالي؟
وفقًا لتبايني في صفحة البلاك جاك ، استنادًا إلى قواعد ستريب الليبرالية، فإن الاحتمالات التالية هي الفوز الصافي أو التعادل أو الخسارة:
- الفوز — 42.43%
- ادفع — 8.48%
- الخسارة — 49.09%
دعونا نتجاهل التعادلات، مما يمنحنا احتمال الفوز، نظرا لليد التي تم حلها في الفوز الصافي أو الخسارة، بنسبة 46.36٪.
دعونا نستخدم 100 يد في الساعة كسرعة للعب.
يمكننا تقريب احتمال رؤية سلسلة واحدة على الأقل من 60 يدًا على الأقل على التوالي على النحو التالي:
100×12×0.4636 60 = 1 في 89,412,355,233,588,500.وكأساس للمقارنة، إذا قمت بشراء تذكرة Powerball وتذكرة Megamillions واحدة، فإن احتمال الفوز بكلتا التذكرتين سيكون 1 من 88,412,922,115,818,300.
لذا فإن احتمالية الفوز باليانصيبين ستكون أعلى قليلاً من رؤية 60 فوزًا متتاليًا في 12 ساعة من اللعب.


