اسأل الساحر #355
في فيلم "رخصة للقتل"، يلعب جيمس بوند ثلاث جولات من البلاك جاك، بخمس أوراق في كل مرة. لاحظتُ أنه لم يُفلح في أيٍّ منها. ما احتمالات ذلك؟
يمكنك العثور على مقطع من المشهد على اليوتيوب .
تحتوي اللعبة على عدد كبير من البطاقات الكبيرة، أليس كذلك؟ هذه هي البطاقات التي استطعتُ تمييزها. مع العلم أنه في بعض الحالات، لم تكن البطاقات واضحة.
رخصة القتل - الرتب المرصودة
| رتبة | لاحظ |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| ج | 3 |
| س | 6 |
| ك | 4 |
| أ | 1 |
| المجموع | 35 |
أنت محقٌّ تمامًا، بوند لم يُحقق أيًّا من أوراقه الخمسة عشر الأولى. قسّم أوراقه الثمانية مرةً واحدة، لكنه لم يُحقق أيَّ نتيجة بعد التقسيم أيضًا. إليك عدد أوراقه الأولى في جميع أوراقه الخمسة عشر:
- مزدوج — 1
- انقسام — 1
- الحامل — 13
فيما يلي احتمالات الاستراتيجية الأساسية لكل إجراء أولي، بافتراض وجود ستة مجموعات من البطاقات، ومضاعفة الرهان بعد السماح بالتقسيم، وإلقاء نظرة خاطفة على البطاقة المخفية، ووقوف الموزع على 17 ناعمة.
بلاك جاك - احتمالات الفعل الأول
| فعل | احتمال |
|---|---|
| يقف | 43.46% |
| يضرب | 39.78% |
| مزدوج | 9.53% |
| ينقسم | 2.48% |
| بلاك جاك | 4.75% |
| المجموع | 100.00% |
إذا سُمح بالاستسلام، فإن هذا الاحتمال سيكون 4.14%، خارج احتمال الوقوف.
تجدر الإشارة إلى أن بوند كان يقف على ١٦ مقابل ١٠. الاستراتيجية الأساسية هي الفوز بهذه الورقة، لكنها ضئيلة جدًا. نظرًا لكثرة أوراق العشرة التي ظهرت في تلك الجولة، ربما كان بوند يعلم أن العدد مرتفع، مما يُفعّل استثناءً في الاستراتيجية الأساسية، وهو الوقوف في هذه الحالة.
احتمال عدم الفوز بأي يد هو 60.22%. واحتمال عدم الفوز بـ 15 من أصل 15، بافتراض أن كل يد مستقلة، هو 0.602162 15 = 0.000496253 = تقريبًا 1 في عام 2015.
في لعبة الحبار، يتنافس 16 لاعبًا على جسر زجاجي. يُقسّم الجسر إلى 18 زوجًا من الزجاج. في كل زوج، قطعة زجاج واحدة مُقسّاة تتحمل وزن اللاعب. أما القطعة الأخرى فهي زجاج عادي، وتنكسر تحت وطأة اللاعب. إذا داس لاعب على قطعة زجاج عادي، سينكسر ويسقط حتفه.
يتعين على اللاعبين التقدم، واحدًا تلو الآخر، وفقًا لترتيب محدد مسبقًا.
بافتراض التخمين العشوائي في كل زوج من الخطوات الزجاجية، ما هو العدد المتوقع للاعبين الذين سيعبرون بأمان؟
سأضع الإجابة والحل في علامات المفسد، للسماح للعالم بالاستمتاع بالعمل على إيجاد الإجابة بأنفسهم.
احتمال عبور اللاعب 1 بأمان هو (1/2)^18 = 1/262144 = تقريبًا 0.000004.
هناك طريقتان يمكن للاعب 2 من خلالهما العبور بأمان:
- اللاعب ١ يعبر بسلام. في هذه الحالة، يستطيع اللاعب ٢ ببساطة تقليد خطواته.
- بين اللاعب 1 واللاعب 2، هناك خطوة خاطئة واحدة فقط. قد تكون هذه الخطوة عند 18 من أزواج الزجاج المحتملة. احتمالية 17 خطوة صحيحة وخطوة خاطئة واحدة هي 18*(1/2)^2 = 18/262144 = 0.000069.
وبالتالي، فإن احتمال عبور اللاعب 2 بأمان هو 0.000004 + 0.000069 = 0.000072.
هناك طريقتان يمكن للاعب 3 من خلالهما العبور بأمان:
- يعبر اللاعب الثاني بأمان. في هذه الحالة، يستطيع اللاعب الثالث ببساطة تقليد خطواته.
- بين اللاعبين ١ و٢ و٣، هناك خطوتان خاطئتان فقط. هناك (combin(18,2)=153 طريقة لاختيار قطعتين من أصل ١٨ زوجًا من الزجاج للقطعتين اللتين ستقتلان اللاعبين ١ و٢. احتمالية ١٦ خطوة صحيحة وخطوتين خاطئتين هي ١٥٣*(١/٢)^٢ = ١٥٣/٢٦٢١٤٤ = ٠.٠٠٠٥٨٤.
وبالتالي، فإن احتمال عبور اللاعب 3 بأمان هو 0.000072 + 0.000584 = 0.000656.
هناك طريقتان يمكن للاعب رقم 4 من خلالهما العبور بأمان:
- اللاعب الثالث يعبر بسلام. في هذه الحالة، يستطيع اللاعب الرابع ببساطة تقليد خطواته.
- بين اللاعبين من ١ إلى ٤، هناك ثلاث خطوات خاطئة فقط. هناك ٨١٦ طريقة لاختيار ٣ من ١٨ زوجًا من الزجاج للقطعتين اللتين ستقتلان اللاعبين من ١ إلى ٣. احتمال ١٥ خطوة صحيحة و٣ خطوات خاطئة هو ٨١٦ × (١/٢)^٢ = ٨١٦/٢٦٢١٤٤ = ٠.٠٠٣١١٣.
وباتباع هذا المنطق، نحصل على الجدول التالي لاحتمالات كل لاعب.
لعبة الجسر
| لاعب | احتمال بقاء |
|---|---|
| 1 | 0.000004 |
| 2 | 0.000072 |
| 3 | 0.000656 |
| 4 | 0.003769 |
| 5 | 0.015442 |
| 6 | 0.048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0.407265 |
| 10 | 0.592735 |
| 11 | 0.759659 |
| 12 | 0.881058 |
| 13 | 0.951874 |
| 14 | 0.984558 |
| 15 | 0.996231 |
| 16 | 0.999344 |
| المجموع | 7.000076 |
للتعبير عن الإجابة بصيغة مغلقة، فهي:
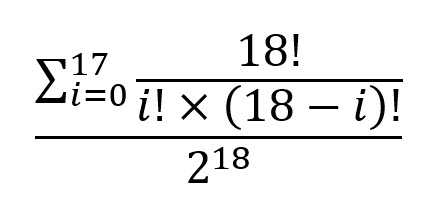
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في لعبة Ultimate X Gold ، عند النقطة 3:10، تحصل على بات فول هاوس، ثلاثة على أربعة. كان مضاعفك لأي أربعة من نفس النوع من 2 إلى 4 هو 9x. كان مضاعف الفل هاوس هو 1x. لماذا احتفظت بالبات فول هاوس، بدلاً من مجرد ثلاثة 3s وحاولت الحصول على أربعة من نفس النوع باستخدام المضاعف الكبير؟
أنت على حق، لقد أفسدت الأمر تمامًا بهذه اليد.
أذكر أنني كنت ألعب ١٠ مرات. وبالتالي، كان ربحي مع امتلاكي للفول هاوس ١٠ × ٣٥ = ٣٥٠.
عند حمل الثلاثة فقط، كان لكل يد الاحتمالات التالية:
- أربعة من نفس النوع — 4.26%
- فول هاوس — 6.11%
- ثلاثة من نفس النوع - 89.64%
وفيما يلي المكاسب لكل يد، بعد المضاعفات:
- أربعة من نفس النوع — 1800
- منزل كامل — 35
- ثلاثة من نوع واحد — 15
كان عائدي المتوقع مع الاحتفاظ بالثلاثيات فقط هو (4.26% * 1800) + (6.11% * 35) + (89.64% * 15) = 92.17854. وهذا أعلى بكثير من عائد الفول هاوس البالغ 35. لذا، نعم، لقد ارتكبت خطأً محرجًا في تلك اليد.
تحداني أحدهم بالرهان التالي. عليّ اختيار أي ثلاث رتب من أوراق البوكر القياسية، وكتابة توقعي، مع إخفائه حتى النهاية. على سبيل المثال، 7-آس-2. ثم عرض عليّ أن يراهن بمبلغ متساوٍ على أنه يستطيع تسمية رتبة واحدة على الأقل من رتبتي إذا حصل على ثلاث تخمينات. ما هي احتمالات فوزي؟
للفوز، يجب أن يكون توقع خصمك خاطئًا في جميع التنبؤات الثلاثة. احتمال خطأ التوقع الأول هو ١٠/١٣، واحتمال خطأ التوقع الثاني هو ٩/١٢، لأننا نستطيع استبعاد أول رتبة مُخمَّنة من الاحتمالات. احتمال خطأ التوقع الثالث هو ٨/١١، لأننا نستطيع استبعاد أول رتبتين مُخمَّنتين من الاحتمالات.
يجب أن تتحقق هذه الأمور الثلاثة جميعها للفوز. وبالتالي، فإن احتمالات فوزك هي (١٠/١٣) * (٩/١٢) * (٨/١١) = ٧٢٠/١٧١٦ = ٤١٫٩٦٪.
في حالة المال المتساوي، فإن ميزة المنزل في هذا الرهان، من جانبك، هي 16.08% (آه!).
تم اقتباس هذا السؤال من كتاب الرهانات المقترحة من تأليف أوين إيشيا (رقم 7).


