اسأل الساحر #367
أحب المراهنة على جميع الأرقام في لعبة الكرابس. كم عدد الأرقام الفريدة التي أتوقع الحصول عليها قبل الحصول على 7 أرقام؟
من أجل مصلحة القراء الآخرين، فإن السؤال يسأل عن عدد الإجماليات التالية التي سيتم الحصول عليها عند رمي حجري نرد قبل الحصول على إجمالي سبعة: 4، 5، 6، 8، 9، و10.
الإجابة هي ٢٫٣٧٥٧٥٨. يوضح الجدول التالي احتمالية كل احتمال فردي لرمي النرد من صفر إلى ستة إجماليات فريدة ضمن النطاق المحدد. تُظهر الخلية السفلية اليمنى متوسط الإجماليات الفريدة التي تم رميها قبل الرقم سبعة.
أرقام فريدة تم تسجيلها
| المجموع | احتمال | مُتوقع |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| المجموع | 1.000000 | 2.375758 |
هل صحيح أن رمي العملة العادلة من المرجح أن يهبط على الجانب الذي بدأ به وجهه لأعلى؟
وتشير الأدلة إلى أن هذا صحيح!
سجل بيرسي دياكونيس وسوزان هولمز من جامعة ستانفورد ١٠٠٠٠ رمية عملة معدنية. استقرت العملة المعدنية على نفس الوجه الذي بدأت به، ووجهها لأعلى، في ٥٠.٨٪ من المرات (المصدر: حل واحد وخمسون بالمائة من النشرة الإخبارية "ما يحدث في العلوم الرياضية" الصادرة عن الجمعية الرياضية الأمريكية). احتمال أن تكون النسبة مرتفعة أو أعلى هو ٥.٤٨٪.
لإثبات ذلك رياضيًا، افترضتُ أن العدد الفعلي لدورات العملة المعدنية يتبع توزيع بواسون. وبشكل أكثر تحديدًا، إذا كان متوسط عدد الدورات m، فإن احتمالية دوران n دورة بالضبط هي exp(-m)*m^n/n!. ولتوضيح توزيع بواسون، يوضح الرسم البياني التالي احتمالية دوران من 0 إلى 25 دورة، بمتوسط 10.
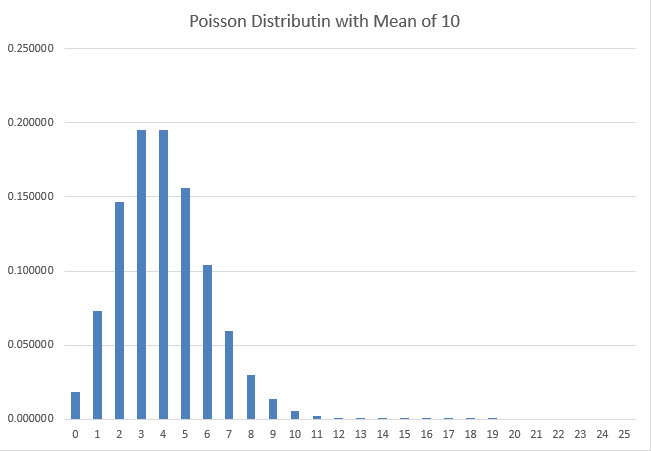
السبب الذي جعلني أختار افتراض بواسون هو أنه يتبع شكل منحنى الجرس القريب لمتوسطات كبيرة بما فيه الكفاية والنتيجة الفعلية لا يمكن أن تنخفض أبدًا عن الصفر.
ثم حسبتُ احتمالية عدد زوجي من أنصاف الدورات (مما يؤدي إلى هبوط نفس الجانب ووجهه لأعلى كموضع البداية) لمتوسطات مختلفة لأنصاف الدورات. يوضح الجدول التالي النتائج لمتوسطات تتراوح بين 0.5 و5.0.
احتمالية عدد الدورات الزوجي والفردي
| الثورات المتوسطة | مجموع زوجي | المجموع الفردي |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
ثم تساءلتُ لماذا كان احتمال العدد الزوجي دائمًا أكبر من ٥٠٪. اتضح أن احتمال العدد الزوجي، بمتوسط m، يمكن التعبير عنه بالمعادلة ٠٫٥ + e^(-٢m)/٢. يجب أن يكون e مرفوعًا للقوة أيًا كان موجبًا، وبالتالي يكون احتمال العدد الزوجي للدورات موجبًا أيضًا.
يمكنك رؤية دليلي على هذه الصيغة هنا .
ما هو تحليلك للعبة Spelling Bee على Price is Right؟
من أجل مصلحة القراء الآخرين، دعوني أستعرض القواعد أولاً.
- هناك لوحة بها 30 بطاقة مرقمة من 1 إلى 30.
- على ظهر كل بطاقة حرف أو كلمة "سيارة". توزيع كل منها كالتالي:
- ج: 11
- أ: 11
- ر: 6
- السيارة: 2
- يسمح المضيفون للاعب باختيار بطاقتين.
- بعد لعبة التسعير، والتي لن أتطرق إليها، تتاح للاعب الفرصة لكسب ما يصل إلى ثلاث بطاقات أخرى.
- سيتم قلب البطاقات.
- يمكن للاعب الفوز بالسيارة بإحدى الطريقتين:
- يحصل اللاعب على بطاقة واحدة على الأقل من كل حرف (وبالتالي تهجئة كلمة CAR).
- يحصل اللاعب على بطاقة "CAR" واحدة على الأقل.
- في أي وقت أثناء اللعبة، يمكن للاعب الاستسلام والحصول على 1000 دولار مقابل كل بطاقة لم يقلبها.
إليكم مقطع من اللعبة التي يتم لعبها.
يوضح الجدول التالي احتمالات الفوز، وفقًا لعدد البطاقات التي يمتلكها اللاعب، على افتراض أنه لم يتم قلب أي منها بعد.
مسابقة التهجئة - احتمال الفوز
| بطاقات | احتمال الفوز |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
قبل قلب أي بطاقة، يجب على اللاعب عدم الاستسلام، بافتراض أي قيمة معقولة للسيارة. على سبيل المثال، حتى مع بطاقتين فقط، تبلغ احتمالية حصول اللاعب على واحدة على الأقل من بطاقات CAR 13.1%. يجب ألا يكترث اللاعب بقيمة الاستسلام البالغة 2000 دولار إذا كانت قيمة السيارة 15,263.16 دولارًا. أي سيارة جديدة ستكون قيمتها أعلى من ذلك.
وفيما يلي نقاط اللامبالاة في قيمة السيارة، وفقًا لعدد البطاقات غير المقلوبة التي يمتلكها اللاعب.
مسابقة التهجئة - احتمال الفوز
| بطاقات | اللامبالاة نقطة |
|---|---|
| 2 | 15,263.16 دولارًا |
| 3 | 8,066.23 دولارًا |
| 4 | 6,849.11 دولارًا |
| 5 | 6,803.75 دولارًا |


