WOO logo

يوصي المعالج

اسأل الساحر #370

نصيحتك بالسعي وراء القيمة في لعب اليانصيب سيئة للغاية! من الواضح أنك لا تفهم أن لاعبي اليانصيب لا يهتمون بالاحتمالات أو القيمة، بل يريدون فقط فرصة، أي فرصة، للفوز بجائزة كبرى كبيرة، ولا يكترثون بالجوائز الصغيرة.

Anonymous

نصيحتي لجميع أنواع المقامرة هي تعظيم ما يمكن للاعب أن يتوقعه من رهانه. خلال 25 عامًا من تحليلي للمقامرة، كانت هذه السياسة ناجحة بالنسبة لي، وأنت أول من يهاجمني بسببها.

مع ذلك، أنا دائمًا منفتح على مراعاة وجهات نظر أخرى. في هذا السياق، لنأخذ لاعبًا يهتم بالإثارة والقيمة على حد سواء. لن يرضى هذا اللاعب بالألعاب منخفضة التقلبات، بل يرغب في الفوز بالثريا بأكملها أو الخسارة أثناء المحاولة. لقياس أي رهان لمثل هذا اللاعب، أنشأتُ إحصائية أُطلق عليها "معامل الإثارة". أُعرّفها بأنها نسبة الانحراف المعياري إلى عنصر المخاطرة. للتذكير، عنصر المخاطرة هو نسبة الخسارة المتوقعة للاعب إلى متوسط مبلغ الرهان في نهاية الجولة (بما في ذلك الرهانات اللاحقة مثل مضاعفة الرهان في البلاك جاك وزيادة الرهان في أنواع البوكر المختلفة).

يوضح الجدول التالي نسبة الإثارة لمجموعة متنوعة من ألعاب ورهانات الكازينو، مرتبة من الأعلى إلى الأدنى. ويُظهر الجدول بالفعل أن لعبة ميجا مليونز تُقدم أقصى قدر من الإثارة للاعب الباحث عن الإثارة.

حاصل الإثارة

لعبة رهان معيار
انحراف		 عنصر
من المخاطر		 الإثارة
الحاصل
ميجا ملايين جائزة كبرى بقيمة 40 مليون دولار، بدون Megaplier* 1158.38 0.8104 1429.38
فيديو بوكر 25-15-9 ديوسيز وايلد 5.06 0.0109 465.68
فيديو كينو كينو اختيار 8: جدول الدفع 2، 12، 98، 1652، 10000 29.96 0.0769 389.56
بلاك جاك قواعد الحد الأدنى الليبرالية** 1.15 0.0049 236.60
الروليت لعبة الصفر المزدوج، رهان رقم واحد 5.76 0.0526 109.49
الباكارات رهان المصرفي 0.93 0.0106 87.74
كرابس خط المرور 1.00 0.0141 70.71
باي غاو بوكر تاجر مصرفي، طريق المنزل 0.75 0.0272 27.57
الروليت لعبة الصفر المزدوج، رهان المال المتساوي 1.00 0.0526 18.97

*: لا يأخذ خط Mega Millions في الاعتبار المعاش التقاعدي أو الضرائب.
**: تفترض لعبة البلاك جاك وجود ستة مجموعات من البطاقات، ويدفع البلاك جاك 3-2، ويضرب الموزع 17 ناعمة، ويسمح بالمضاعفة بعد التقسيم، ويسمح بالاستسلام، ويسمح بإعادة تقسيم الآسات.

شكرا على التعليق وعلى الإهانة.

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

يتم توزيع ثلاث نقاط بشكل عشوائي وموحد على طول دائرة نصف قطرها 1. ما هي المسافة الدنيا المتوقعة بين النقاط الثلاث، حيث يتم قياس المسافات على طول المحيط؟

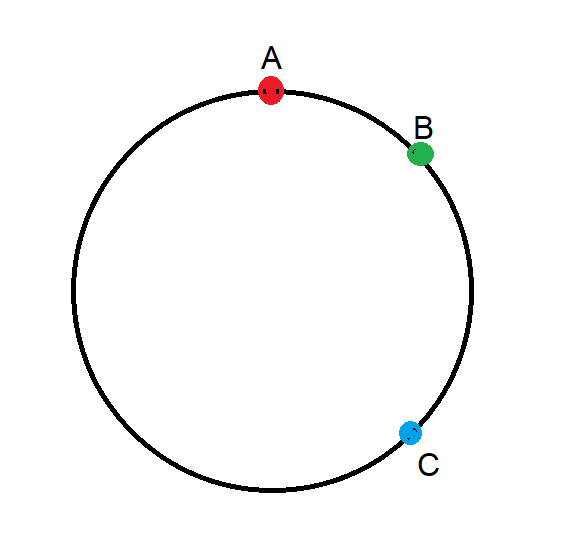
ثلاث نقاط على الدائرة 2

مجهول

الإجابة هي 2*pi/9 =~ 0.698131701.

وهنا الحل الخاص بي (PDF).

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

المقطع العرضي للسقيفة عبارة عن مربع طوله عشرة أقدام وعرضه عشرة أقدام. تقع السقيفة في وسط حقل مفتوح ومستوٍ.

ماعز مربوط في زاوية من الحظيرة بحبل طوله أربعون قدمًا. لا يُسمح للماعز بدخول الحظيرة.

ما هي المنطقة التي يجوز للماعز أن يرعى فيها؟

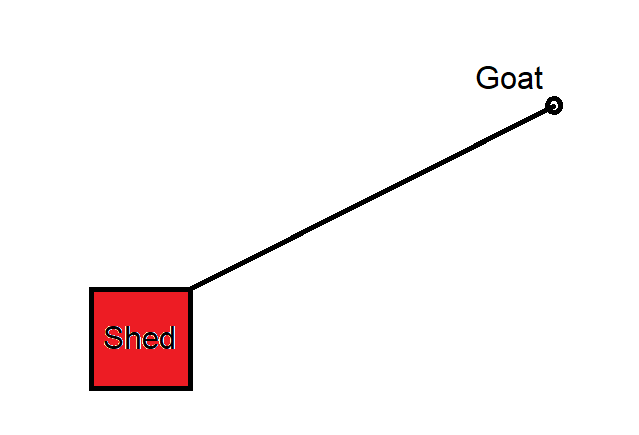
لغز الماعز

Gialmere

يمكن للماعز أن ترعى مساحة 4847.071825 قدمًا مربعًا.

[spoiler=حل جزئي]

انظر إلى الرسم التخطيطي التالي لأغراض المناقشة.

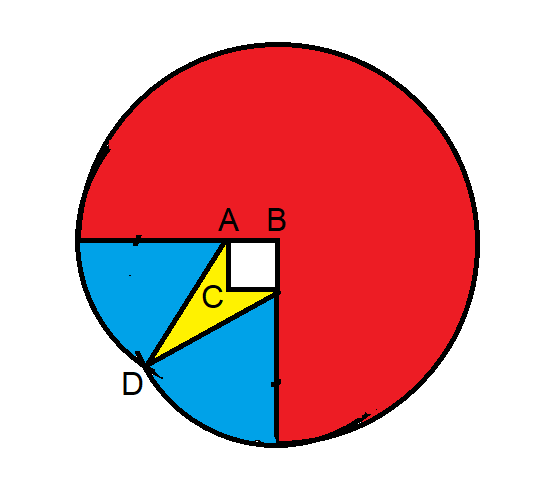
لغز حظيرة الماعز

المساحة التي يمكن للماعز أن ترعى فيها هي مجموع المناطق الحمراء والزرقاء والصفراء.

من المهم حل الزاوية ADC، والتي هي atan(sqrt(2)/sqrt(34)) =~ 0.237941125 راديان.

أرجو المعذرة إذا لم أدخل في التفاصيل، ولكن إليكم مناطق كل منطقة، حسب اللون:

  • الأحمر = 3769.911184
  • أزرق = 921.005359
  • الأصفر = 156.155281
  • المجموع = 4847.071825
[/كابح]

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .