اسأل الساحر #373
أنا متأكد من أنك من مُحبي نظرية الانفجار العظيم. من مشاهدي المُفضلة لعبة حجرة ورقة مقص سحلية سبوك. إنها أشبه بلعبة حجرة ورقة مقص بخمسة رموز، بقواعدها التالية:
- ورق يغطي الصخور
- صخرة تسحق سحلية
- السحلية تسمم سبوك
- سبوك يحطم المقص
- المقص يقطع الورق
- السحلية تأكل الورق سبوك يبخّر الصخور
- مقص يقطع رأس السحلية
- ورقة تدحض سبوك
- الصخرة تسحق المقص
سؤالي هو هل يمكن إضافة المزيد من الرموز، بحيث يكون لكل جانب نفس الفرص ضد لاعب عشوائي؟
نعم، أحب هذا المشهد أيضًا! إليكم فيديو له على يوتيوب .
تحتاج إلى عدد فردي من الرموز. نظريًا، يمكنك الحصول على عدد زوجي، ولكن عليك حينها وضع قواعد تؤدي إلى تعادل أزواج معينة من الرموز المختلفة. لا، نريد لعبة حاسمة حيث يكون التعادل فقط إذا لعب كلا اللاعبين نفس الرمز.
الحل أنيقٌ للغاية وسهل الشرح باستخدام عددٍ أوليٍّ من الرموز. دعوني أشرح باستخدام سبعة رموز، كمثال. لنسمِّ الرموز من A إلى G ونمثلها على دائرة، في الرسم التخطيطي التالي.
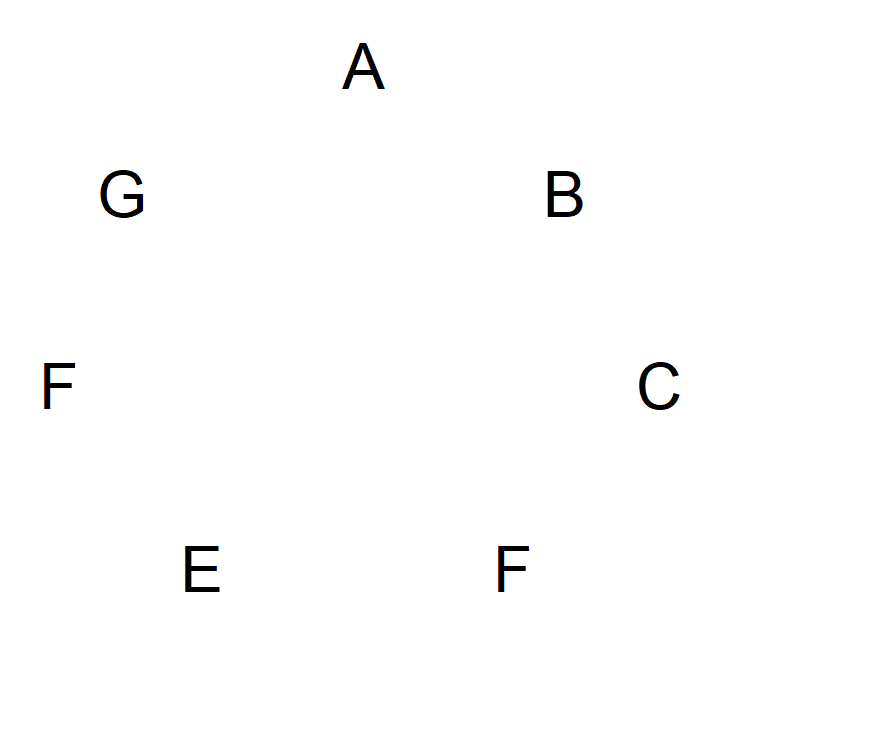
بعد ذلك، ابدأ بالرمز A، ثم ارسم سهمًا للرمز التالي باتجاه عقارب الساعة. يجب أن يشير السهم إلى الرمز الذي يقع بين الرمزين. تخيل الأمر كما لو أن هذا الرمز قد أُطلق عليه سهم. استمر في الحركة باتجاه عقارب الساعة حتى تصل إلى A. لن يبدو الرسم التخطيطي كما يلي:
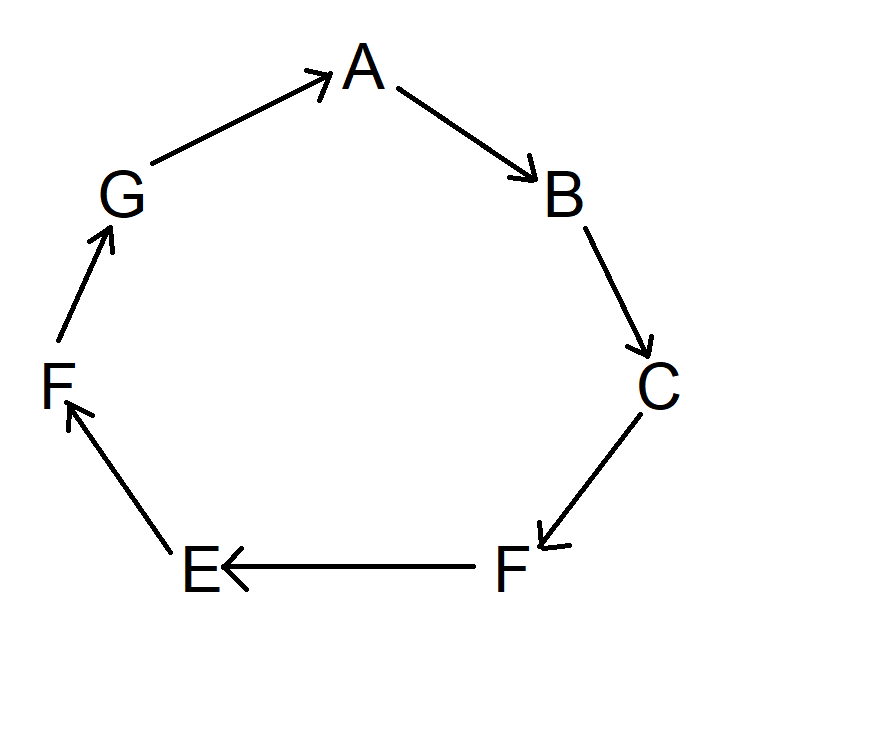
بعد ذلك، كرر نفس العملية، ولكن بحركة رمزين باتجاه عقارب الساعة، بدءًا من A. في الواقع، يمكنك البدء من أي مكان تريده. يبدو الرسم التخطيطي الآن كما يلي:
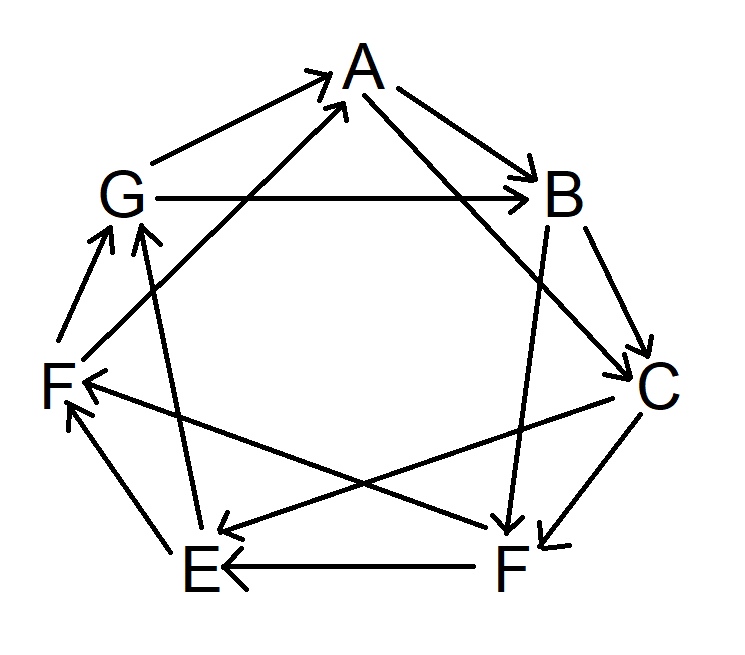
أخيرًا، كرر العملية نفسها، ولكن تخطى ثلاثة رموز باتجاه عقارب الساعة. سيبدو الرسم التخطيطي الآن كما يلي:
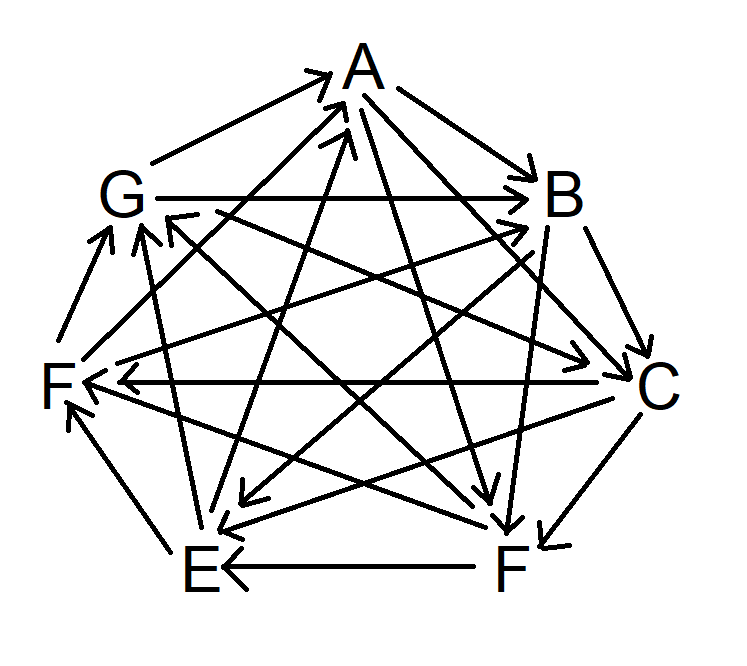
لاحظ في هذه المرحلة أن كل رمز يتغلب على ثلاثة رموز أخرى ويتغلب عليه ثلاثة رموز أخرى مختلفة.
هذه الطريقة فعّالة لأي عدد أولي من الرموز، لأنك عند العودة إلى الرمز الأصلي ستكون قد مررت بجميع الرموز. بالنسبة لـ n رمز، ستحتاج إلى تكرار هذه العملية (n-1)/2 مرة.
يمكنك إنشاء لعبة متوازنة بأي عدد فردي من الرموز، ولكنك ستعود إلى الرمز الأصلي بسرعة كبيرة أحيانًا. عند حدوث ذلك، سيتعين عليك إعادة تكرار الحلقات بدءًا من الرموز التي فاتتك.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ما هو احتمال التعادل في لعبة البوكر ذات الثلاث بطاقات؟
الإجابة الدقيقة هي 450528/407170400 =~ 0.001106485 =~ 1/904.
يوضح الجدول التالي عدد طرق تكوين كل نوع من اليد الأولى وعدد التركيبات التي تتعادل في اليد الثانية. في حالة اليد المستقيمة واليد المتعادلة، يُهم وجود مجموعتين أو ثلاث مجموعات في اليد الأولى.
تُظهر الخلية أسفل اليمين وجود 450,528 طريقة للتعادل في لعبة البوكر بثلاث أوراق. العدد الإجمالي للمجموعات لليدين هو combin(52,3)*combin(49,3) = 407170400. وبالتالي، يكون الناتج 450528/407170400.
ربطة عنق بوكر بثلاث بطاقات
| يُسلِّم | اليد 1 | اليد 2 | منتج |
|---|---|---|---|
| ثلاثة من نفس النوع | 52 | 0 | 0 |
| فلاش مستقيم | 48 | 3 | 144 |
| مستقيم (ثلاثة بدلات) | 288 | 26 | 7,488 |
| مستقيم (بدلتين) | 432 | 25 | 10,800 |
| تدفق | 1,096 | 3 | 3,288 |
| زوج | 3,744 | 3 | 11,232 |
| خردة (ثلاث بدلات) | 6,576 | 26 | 170,976 |
| خردة (بدلتين) | 9,864 | 25 | 246,600 |
| المجموع | 22,100 | 450,528 |
ما هي قيمة قسيمة الآس المجانية في لعبة بلاك جاك 6-5؟
في قيمة صفحتي المجانية أذكر أن قيمتها هي 50.1844% من مبلغ الرهان في لعبة البلاك جاك 3-2.
في لعبة بلاك جاك بستة مجموعات، احتمال الفوز ببلاك جاك، بشرط أن تكون الورقة الأولى هي الآس، هو 29.3139%. عند حدوث ذلك، تربح 0.3 وحدة أقل في بلاك جاك 6-5 مقارنةً بـ 3-2.
وبالتالي فإن قيمة الآس المجاني في لعبة بلاك جاك 6-5 المكونة من ستة طوابق هي 50.1844% × 29.3139 × 0.3 = 41.3902% من الرهان الأولي.
تحداني أحدهم في رهان على أنه يستطيع الحصول على ١٢ نتيجة باستخدام نردين خلال ٢٧ رمية. لو لم يفعل، لكنت ربحت مبلغًا متساويًا. بما أن احتمال الحصول على ١٢ هو ١/٣٦، ألا يجب أن يحتاج ٣٦ رمية في المتوسط للحصول على ١٢؟ يبدو أن الاحتمالات كانت في صالحي لو أن خصمي حصل على ٢٧ رمية فقط. هل أنا محق، أم أين الخطأ في حساباتي؟
متوسط وقت الانتظار بين رميات الـ ١٢ هو ٣٦ رمية، بما في ذلك رمية الـ ١٢ نفسها. مع ذلك، هذا لا يعني أنها تأتي كل ٣٦ رمية بالضبط. احتمال عدم ظهور ١٢ هو (٣٥/٣٦). واحتمال عدم ظهوره بعد ٢٧ رمية هو (٣٥/٣٦)^٢٧. لذا، فإن احتمال ظهور ١٢ على الأقل هو ١-(٣٥/٣٦)^٢٧ = ٥٣.٢٦٪.
يوضح الجدول التالي احتمالية الحصول على ١٢ على الأقل من ٢٠ إلى ٣٦ رمية. تجدر الإشارة إلى أن الحصول على ٢٥ رمية ضروري لتحقيق أفضلية عند تساوي قيمة العملة.
الاحتمال 12
| لفات | احتمال |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |


