اسأل الساحر #379

يوضح الجدول التالي الكلمة الثانية الموصى بها، بناءً على أدائك بعد لعب STARE. أدرج جميع الحالات التي يكون فيها مجموع درجات الأصفر والأخضر من ٠ إلى ٢. في حالتين، لم أجد كلمة صحيحة.

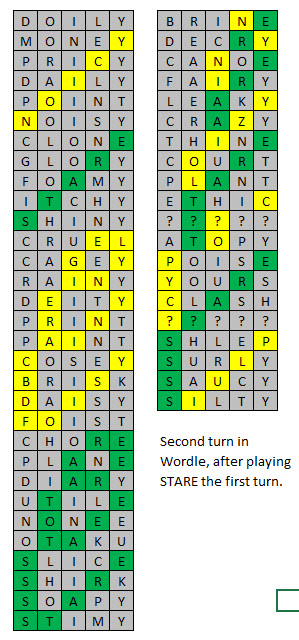
على سبيل المثال، إذا كانت نتيجة STARE هي الحصول على اللون الأصفر فقط في الموضع الخامس (من اليسار)، فقم بلعب MONEY في دورك الثاني.

نصيحتي تعتمد في الغالب على الكلمة التي تحتوي على الأحرف الأكثر استخدامًا، وخاصةً في تلك المواضع. مع ذلك، راعيتُ أيضًا الكلمات التي أستخدمها. للاطلاع على قائمة بأفضل عشر كلمات مناسبة للمواقف، يُرجى الاطلاع على منشوري حول هذا الموضوع على موقع Wizard of Vegas .

بالنسبة لأولئك الذين ليسوا على دراية به، يعمل Doey Don't على النحو التالي:

1. في لفة الخروج، قم بوضع رهان المرور ورهان عدم المرور، بنفس المبلغ.
2. إذا تم الحصول على نقطة، راهن على الاحتمالات المتعلقة بها.

الفكرة هي أن رهان "عدم المرور" يُمثل حماية من الحصول على 7 نقاط في رمية "الخروج". اللاعبون الذين يلعبون رهان "عدم المرور" غالبًا ما يُفضلون عدم التوازن، مما يسمح للاعب بالاستمتاع برهان الاحتمالات دون أي ميزة للكازينو.

العيب هو أنه إذا رُمي الرقم ١٢ في رمية الخروج، فسيخسر اللاعب الذي يُمرر، وسيُدفع اللاعب الذي لا يُمرر، مما يؤدي إلى خسارة وحدة واحدة. احتمال الحصول على ١٢ هو ١/٣٦، مما يجعل الخسارة المتوقعة بهذه الاستراتيجية ١/٣٦ = ٢.٧٨٪ من وحدة واحدة. في المقابل، الخسارة المتوقعة عند وضع رهان مرور فقط مع أخذ احتمالات ٧/٤٩٥ = ١.٤١٪ من وحدة واحدة.

مع ذلك، يتميز مؤشر Doey Don't بتقلبات أقل. بافتراض احتمالات 3-4-5x، إليك الانحراف المعياري في كلا الاتجاهين:

• احتمالات النجاح + الكاملة: 4.915632
• لا تفعل: 4.085789

خلاصة القول هي أنني لا أوصي بـ Doey Don't، لأن الخسارة المتوقعة هي 1.36% من الوحدة أكثر.

> [spoiler=الحل]

يترك:

• p = احتمال الحصول على الرقم 12 أولاً من الحالة الأولية أو في أي وقت لم تكن فيه الرمية السابقة 7.
• س = احتمال ظهور الرقم 12 أولاً عندما كانت الرمية السابقة هي 7.

وهذا ما يُعرف بمشكلة سلسلة ماركوف.

قبل أن نصل إلى ذلك، تذكر أن احتمال الحصول على مجموع 7 هو 1/6، واحتمال الحصول على مجموع 12 هو 1/36.

يمكننا تعريف p و q من حيث بعضهما البعض، على النحو التالي:

• (1) ص = (1/36) + (6/36)س + (29/36)ص
• (2) س = (1/36) + (29/36)ص

دعونا نضرب المعادلة (1) في 36:

36p = 1 + 6q + 29p
(3) 7p = 1 + 6q

دعونا نستبدل قيمة q في (2) في (3):

7ع = 1 + 6*((1/36) + (29/36)ع)
7p = 1 + (1/6) + (29/6)p
42 بنسًا = 6 + 1 + 29 بنسًا
13 ب = 7
س = 7/13

لذا، فإن احتمال الحصول على الرقم 12 أولاً هو 7/13 =~ 53.85%.

وبالتالي فإن احتمال الحصول على الرقم 7 مرتين متتاليتين أولاً هو 46.15%.

وبالتالي، فمن الأرجح أن يتم الحصول على المجموع 12 أولاً.