يوصي المعالج
-
$مكافأة ترحيبية بقيمة 11000 -
مكافأة ترحيبية 100% -
$مكافأة ترحيبية بقيمة 3000
اسأل الساحر #391
1 2 + 2 2 + 3 2 + ... + n 2 = ؟
هذا هو الحل الخاص بي. (PDF)
لنفترض أنك رميت عملة معدنية عادية مليون مرة. باستخدام آلة حاسبة بسيطة فقط مع الدوال الحسابية الخمس الأساسية (+، 0، *، /، ^)، ما هو احتمال الحصول على نفس عدد النقش والكتابة بالضبط؟ يكفي تقدير دقيق.
تذكر معادلة المنحنى الطبيعي القياسي:
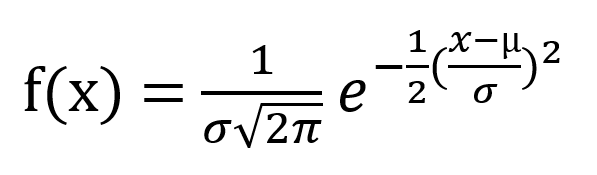
العدد المتوقع لأوراق الكتابة في رمية واحدة هو 0.5، ومربعها هو 0.5 أيضًا. وبالتالي، فإن تباين عدد أوراق الكتابة في رمية واحدة هو 0.5-(0.5) 2 = 0.5 - 0.25 = 0.25. تباين مليون رمية هو 1,000,000 × 0.25 = 250,000. الانحراف المعياري لمليون رمية هو الجذر التربيعي لذلك: sqrt(250,000) = 5,000.
ليكن x = عدد النهايات مقسومًا على العدد المتوقع وهو ٥٠٠,٠٠٠. متوسط x يساوي صفرًا. كما هو موضح، الانحراف المعياري لـ x هو ٥,٠٠٠.
احتمال x=0 هو كالتالي:
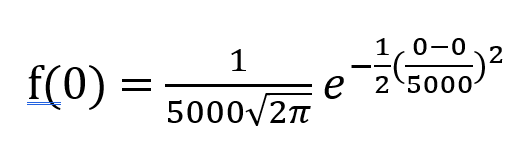
يمكن تبسيط هذا إلى 1/(5000*sqrt(2*π)) =~ 0.000797885 =~ 1 في 1253.314137.
[/كابح]الروابط
مدخل ويكيبيديا عن المنحنى الطبيعي القياسي .
أنت تقود دراجة هوائية على مسار رياضي بسرعة ١٥ ميلًا في الساعة. على المسار، هناك عدّاءون يسيرون بسرعة ٥ أميال في الساعة. عدد العدّائين متساوٍ في كلا الاتجاهين. ما نسبة العدّائين الذين تتجاوزهم والذين يسيرون في الاتجاه المعاكس لك؟
افترض أن طول المسار هو 15 ميلاً.
كان راكب الدراجة يواجه عدّائين يبدؤون من الجانب الآخر في أي وقت من 3 ساعات قبل أن أبدأ إلى ساعة بعد ذلك، بإجمالي 4 ساعات من العدّائين الذين قابلتهم.
عند السير في نفس الاتجاه، كان راكب الدراجة يواجه عدّائين غادروا قبل ساعتين مني في نفس الوقت، بإجمالي ساعتين.
وبالتالي، سيتضاعف عدد العدّائين السائرين في الاتجاه المعاكس. نسبة العدّائين السائرين في الاتجاه المعاكس إلى جميع العدّائين هي 4/(2 + 4) = 2/3.
[/كابح] [spoiler=الحل رقم 2]بالنسبة للعدائين الذين يسيرون في نفس الاتجاه، سرعتك هي 15-5 = 10 ميل في الساعة.
بالنسبة للعدائين الذين يسيرون في الاتجاه المعاكس، سرعتك هي 15 + 5 = 20 ميلاً في الساعة.
إذن، ستمرّ بضعف عدد العدّائين السائرين في الاتجاه المعاكس. وهذا يُنتج نسبة ٢/(١ + ٢) = ٢/٣.
[/كابح]تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .