اسأل الساحر #395
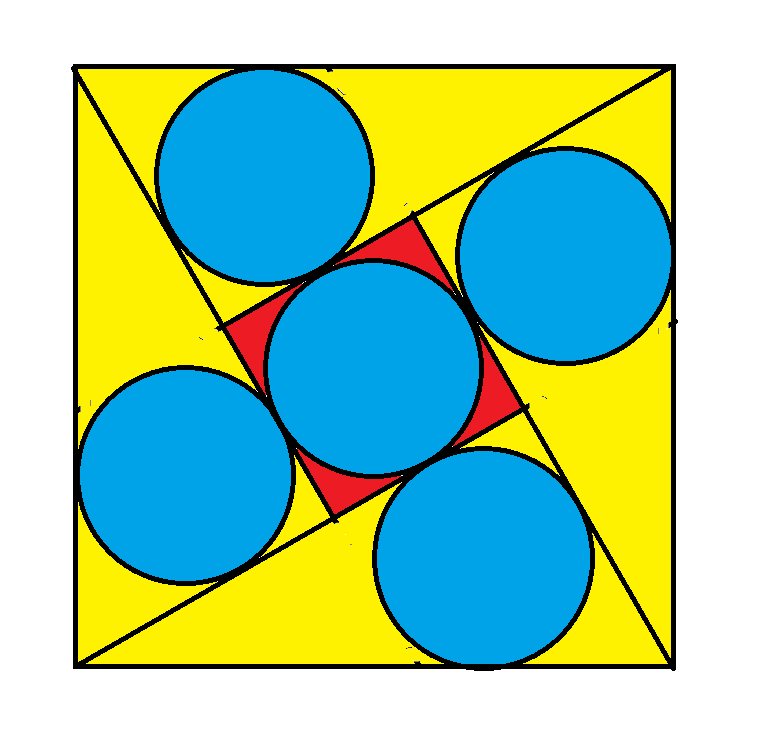
يتكون الرسم البياني أعلاه من أربعة مثلثات قائمة ومربع صغير داخل مربع كبير. طول ضلع المربع الكبير يساوي 1. جميع الدوائر الخمس لها نفس القطر. ما هو نصف قطر هذا المربع؟
نصف القطر = (الجذر التربيعي (3) - 1) / 4 = ~ 0.183013.
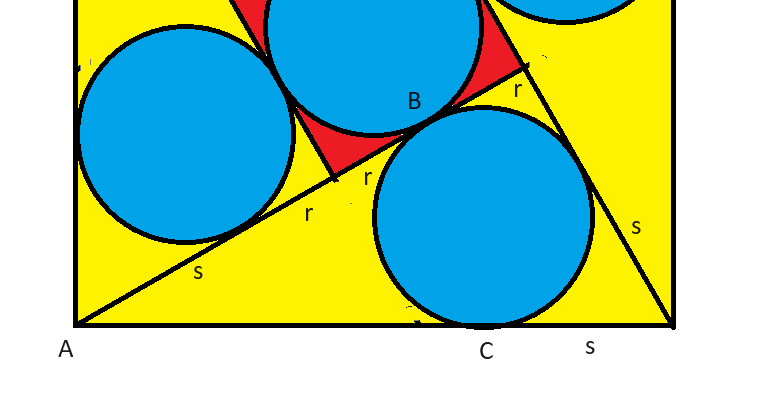 لننظر إلى أحد المثلثات. لنُعرّفه:
لننظر إلى أحد المثلثات. لنُعرّفه:- r = نصف قطر الدوائر
- س = المسافة بين أي زاوية من زوايا المربع الكبير وأقرب دائرة تكون مماسة للمثلث المرسوم فيه.
عند النظر إلى المثلث في الصورة فإن المسافات هي:
- الساق القصيرة = r+s
- الساق الطويلة = 3r+s
- الوتر = 1
باستخدام صيغة فيثاغورس:
(r+s) 2 + (3r+s) 2 = 1
r 2 + 2rs + s 2 + 9r 2 + 6rs + s 2 = 1
10r 2 + 2s 2 + 8rs = 1
نحتاج إلى معادلة أخرى لحل هذه المسألة. لننظر إلى طول المربع الكبير، وهو ١. AB = AC. AB = ٢r+s، إذًا AC = ٢r+s. طول باقي ضلع المربع الكبير هو s. إذًا:
2r + 2s = 1.
2س = 1-2ر
س = 1/2 - ر
دعونا ندخل ذلك في معادلتنا من صيغة فيتاغورس:
10r 2 + 2(1/2 - r) 2 + 8r(1/2 - r) = 1
10ص 2 + 2(1/4 - ص + ص 2 ) + 4ص - 8ص 2 = 1
2ر 2 + 1/2 - 2ر + 2ر 2 + 4ر = 1
4r 2 + 2r - 1/2 = 0
8r 2 + 4r - 1 = 0
باستخدام المعادلة التربيعية:
r = (-4 +/- الجذر التربيعي (48))/16
ص = (جذر(3)-1)/4 =~ 0.183013.
هذه المسألة مأخوذة من قناة "انتبه لقراراتك" على يوتيوب. يقدم بريش حلاً لا يتطلب صيغة فيثاغورس.
[/spoiler]
تم طرح هذه المشكلة ومناقشتها في المنتدى الخاص بي في Wizard of Vegas .
ما رأيك في "نظام الصواب والخطأ"؟ آلية عمله هي أن يضع اللاعب رهان "عدم المرور" بوحدة واحدة. إذا ظهرت أي نقطة، يراهن اللاعب بوحدة واحدة على الرقم. إذا ظهر الرقم، يحقق اللاعب ربحًا، وإذا خرج بسبعة، يحقق التعادل. يبدو هذا وكأنه لعبة مجانية. ما الذي أغفله؟
لنفترض بسخاء أنه إذا كانت النتيجة 4 أو 10، فإن اللاعب يدفع عمولة 5% على الفوز فقط. سنتبع قاعدة فيغاس، حيث يُعدّ الحصول على 12 في رمية الخروج رهانًا سلبيًا في رهان عدم المرور (في شمال نيفادا، يُدفع على الرقم 2). مع ذلك، إليك جميع النتائج المحتملة:
- تخرج لفة 2 أو 3: يفوز اللاعب بوحدة واحدة في حالة الرهان على عدم المرور.
- تخرج لفة 12: اللاعب يدفع لا يمر الرهان.
- خروج رمية 7 أو 11: يخسر اللاعب رهان عدم المرور.
- نقطة 4 أو 10 ونقاط الفوز: يفوز اللاعب بـ 1.95 وحدة على رهان الشراء ويخسر وحدة واحدة على عدم المرور ليحقق فوزًا صافيًا قدره 0.95 وحدة.
- نقطة 5 أو 9 ونقاط الفوز: يفوز اللاعب بـ 1.4 وحدة على رهان المكان ويخسر وحدة واحدة على عدم المرور للفوز الصافي بـ 0.4 وحدة.
- نقطة 6 أو 8 ونقاط الفوز: يفوز اللاعب بـ 7/6 وحدات على رهان المكان ويخسر وحدة واحدة على عدم المرور للفوز الصافي بـ 1/6 وحدات.
- نقطة 4 أو 10 وخسارة النقطة: يخسر اللاعب وحدة واحدة عند شراء الرهان ويفوز بوحدة واحدة عند عدم المرور للدفع الصافي.
- نقطة 5 أو 9 وخسارة النقطة: يخسر اللاعب وحدة واحدة عند وضع الرهان ويفوز بوحدة واحدة عند عدم المرور للدفع الصافي.
- نقطة 6 أو 8 وخسارة النقطة: يخسر اللاعب وحدة واحدة عند وضع الرهان ويفوز بوحدة واحدة عند عدم المرور للدفع الصافي.
يُلخص الجدول التالي جميع النتائج المحتملة. يُظهر الجدول احتمالية وربح ومساهمة جميع النتائج المحتملة في العائد. تُظهر الخلية اليمنى السفلية خسارة متوقعة قدرها 0.02951 وحدة.
نظام الطريق الصحيح والطريق الخطأ
| حدث | يدفع | احتمال | يعود |
|---|---|---|---|
| اخرج 2 أو 3 | 1 | 0.083333 | 0.083333 |
| اخرج 12 | 0 | 0.027778 | 0.000000 |
| اخرج 7 أو 11 | -1 | 0.222222 | -0.222222 |
| فوز النقطة 4 | 0.95 | 0.027778 | 0.026389 |
| فوز النقطة 5 | 0.4 | 0.044444 | 0.017778 |
| فوز النقطة 6 | 0.166667 | 0.063131 | 0.010522 |
| فوز النقطة 8 | 0.166667 | 0.063131 | 0.010522 |
| فوز النقطة 9 | 0.4 | 0.044444 | 0.017778 |
| فوز النقطة 10 | 0.95 | 0.027778 | 0.026389 |
| خسارة النقطة 4 | 0 | 0.055556 | 0.000000 |
| خسارة النقطة 5 | 0 | 0.066667 | 0.000000 |
| خسارة النقطة 6 | 0 | 0.075758 | 0.000000 |
| خسارة النقطة 8 | 0 | 0.075758 | 0.000000 |
| خسارة النقطة 9 | 0 | 0.066667 | 0.000000 |
| خسارة النقطة 10 | 0 | 0.055556 | 0.000000 |
| المجموع | 1.000000 | -0.029512 |
سبب كون هذه الاستراتيجية ذات قيمة متوقعة سلبية هو عند رمية الخروج. هناك ثلاث طرق للفوز عند الرقمين 2 أو 3، وثماني طرق للخسارة عند الرقمين 7 أو 11. صحيح أن اللاعب إذا نجا من رمية الخروج، فسيكون رصيده إيجابيًا، لكن هذا لا يكفي لتجاوز الخسارة المتوقعة عند رمية الخروج.
زوجتي غاضبة بنسبة ٢٠٪ من الوقت. عندما يُسأل "هل أنت غاضب؟"، تُجيب بـ "لا" بنسبة ٩٠٪ وهي غاضبة. وعندما يُسأل نفس السؤال وهي غير غاضبة، تُجيب بـ "لا" بنسبة ٩٥٪. سؤالي: ما احتمال أن تكون غاضبة بناءً على إجابة السؤال؟
هذا هو سؤال الاحتمالات البايزية الكلاسيكي.
إذا أجابت بـ "لا"، فإن احتمال أن تكون غاضبة هو 9/47 = 19.15%.
إذا أجابت بـ "نعم"، فإن احتمال أن تكون مجنونة هو 1/3 = 33.33%.
الصيغة للإجابة على الأسئلة المعبر عنها بـ "إذا كان أ ثم ب" هي الاحتمال (أ و ب) / الاحتمال (ب).
في حالة الإجابة بـ "لا"، فإن احتمالية أن تكون مجنونة هي (0.2*0.9)/(0.2*0.9 + 0.8*0.95) = 0.18/0.94 = 9/47.
في حالة الإجابة بنعم، فإن احتمالية أن تكون مجنونة هي (0.2*0.1)/(0.2*0.1 + 0.8*0.05) = 0.02/0.06 = 1/3.


