اسأل الساحر #399
إذا أزلتَ المربع الصغير من الصورة الأولى وأعدتَ ترتيب القطع، فستبقى المساحة الكلية كما هي. كيف يُمكن ذلك؟
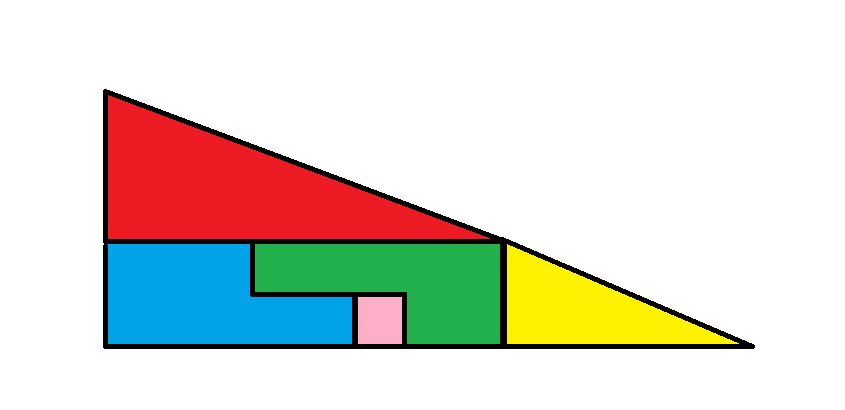
الصورة 1
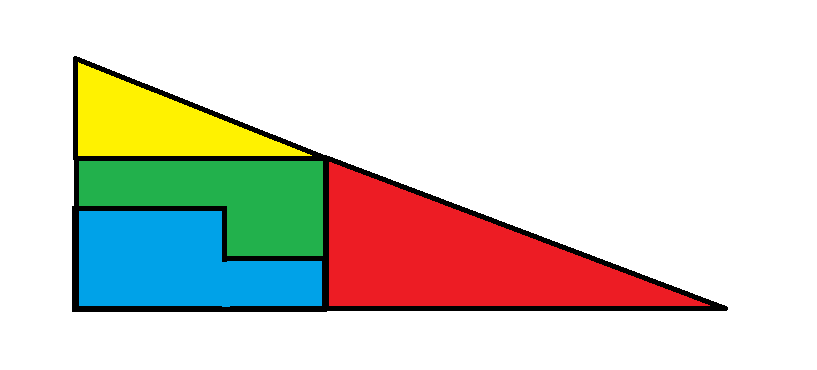
الصورة 2
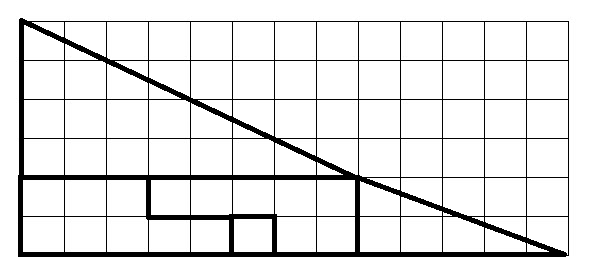
تُظهر الصورة أعلاه الصورة الأولى على الشبكة، لرؤية حجم كل قطعة بشكل أفضل.
لاحظ أن المثلث الأحمر الكبير له ضلعان طولهما 4 و8. لاحظ أيضًا أن المثلث الأصفر الأصغر له ضلعان طولهما 2 و5. بمعنى آخر، المثلثان غير متناسبين. ميل وتر المثلثين ليس هو نفسه كما هو موضح في أي من الشكلين. ميل أحدهما 0.5 والآخر 0.4. وضع القطع كما هي في أي من الشكلين يجعل الشكل يبدو وكأنه مثلث كبير طول ضلعيه 5 و13، ولكنه ليس مثلثًا.
مساحة المثلث الأحمر هي 4*8/2 = 16.
مساحة المثلث الأصفر هي 2*5/2 = 5.
في الصورة الأولى، تشكل القطع الثلاث الأخرى مستطيلًا بحجم 2 × 8، بمساحة إجمالية قدرها 16.
في الصورة الثانية، تشكل القطعتان الأخريان مستطيلًا بحجم 3 × 5، بمساحة إجمالية قدرها 15.
المساحة الكلية للصورة الأولى هي المثلث الأحمر + المثلث الأصفر + المستطيل الكبير = 16 + 5 + 16 = 37.
المساحة الكلية للصورة الثانية هي المثلث الأحمر + المثلث الأصفر + المستطيل الصغير = 16 + 5 + 15 = 36.
في الختام، الصورة الأولى أكبر بمربعها الصغير. إنه وهم بصري أن مجموع القطع يُشكّل مثلثًا كبيرًا في كلتا الحالتين. لكنهما ليسا كذلك.
هناك ١٦ دراجة نارية على حافة صحراء واسعة. تستطيع كل دراجة نارية قطع مسافة ١٠٠ ميل بخزان وقود كامل. تبدأ جميع الدراجات النارية بخزان وقود ممتلئ. يُسمح بنقل الوقود بين الدراجات. الهدف هو إبعاد دراجة نارية واحدة عن نقطة انطلاقها قدر الإمكان. إلى أي مدى يمكنها الوصول؟
مفتاح الحل هو أن تقطع المجموعة مسافة قصيرة. ثم يُملأ خزان الوقود المتبقي من إحدى الدراجات النارية ويُملأ خزانات الدراجات الأخرى.
على سبيل المثال، في البداية، قسّم خزان الوقود الممتلئ إلى ١٦ جزءًا، لكل دراجة نارية جزء. ثم انطلقوا معًا حتى يستهلك ١/١٦ من الخزان، ما يُعطي المجموعة ١٠٠/١٦ = ٦.٢٥ ميل. خذ ١٥/١٦ من خزان إحدى الدراجات النارية، واسحب ١/١٦ منه إلى الدراجات الخمس عشرة الأخرى، مما يُكملها تمامًا.
ثم كرر نفس العملية، ولكن مع بقاء ١٥ دراجة نارية، اقطع مسافة ١/١٥ من خزان الوقود، أي ١٠٠/١٥ = ٦٫٦٦٦٦٦٧ ميلًا. ثم خذ ١٤/١٥ من خزان الوقود من دراجة نارية واحدة، واسحب ١/١٥ من خزان الوقود إلى الدراجات النارية الـ ١٤ الأخرى.
بالاستمرار في هذه العملية، سنحصل على آخر دراجة نارية بمسافة إجمالية (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338.072899 ميل.
تم طرح هذا السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .
ما هي أفكارك حول مفارقة الجميلة النائمة؟
من أجل مصلحة القراء الآخرين، إليكم ما تم طرحه في مشكلة/مفارقة الجميلة النائمة.
تطوّعت الجميلة النائمة (SB) لإجراء تجربة. شُرِحت لها جميع تفاصيل التجربة بصدق، على النحو التالي:
- الأحد: تُخَيَّمُ س.ب. بعد أن تغفو، تُقْرَعُ عملةٌ عادلة.
- الاثنين: ستُوقَظ إس بي يوم الاثنين، ويُسأل: "ما احتمال سقوط العملة على الوجه؟". بعد أن تُجيب، ستُعاد إلى النوم بدواءٍ يُنسيها كل ما حدث يوم الاثنين.
- الثلاثاء: إذا سقطت العملة على ظهرها، فسيتكرر ما حدث يوم الاثنين. إذا سقطت العملة على ظهرها، ستنام طوال اليوم.
- الأربعاء: يتم إيقاظ SB مرة أخرى، ولا يُسأل عن أي شيء، ويعود إلى منزله بعد انتهاء التجربة.
السؤال هو كيف ينبغي لها أن تجيب على السؤال الذي طرح يوم الاثنين وربما يوم الثلاثاء؟
إجابتي
إذا تكررت هذه التجربة مليون مرة، فمن المتوقع أن نرى ثلاثة أنواع من الاستيقاظات، وكل منها متساوية في احتمال حدوثها:
- تهبط العملة المعدنية على الرأس، وتستيقظ يوم الاثنين.
- تهبط العملة المعدنية على ظهرها، وتستيقظ يوم الاثنين.
- تهبط العملة المعدنية على ظهرها، وتستيقظ يوم الثلاثاء.
هذا لأن الاستيقاظ يوم الاثنين يجب أن يُقسّم بالتساوي بين رميات العملة (الصورة والكتابة). أيضًا، إذا استقرت العملة على الكتابة، فسيكون الاستيقاظ يومي الاثنين والثلاثاء متساويًا تمامًا. وبالتالي، سيكون لدى المجموعات الثلاث عدد متساوٍ تقريبًا من الاستيقاظات على عينة كبيرة.
من بين هذه الاستيقاظات، يحدث واحد من كل ثلاثة بعد رمي العملة. وبالتالي، فإن احتمال سقوط العملة على الوجه الآخر هو ١/٣.
يزعم المعسكر نصف أن SB لم يتم تزويده بأي معلومات إضافية عند كل استيقاظ وبالتالي يجب أن يفترض أن كل نتيجة للانقلاب كانت متساوية الاحتمالية.
إلى ذلك، أوسّع نطاق المسألة لتشمل 999,999 استيقاظًا إذا استقرت العملة على وجه الكتابة. سيحدث استيقاظ واحد فقط من كل مليون بعد رمي العملة على وجه الكتابة. لذا، من السهل جدًا افتراض أنه في أي استيقاظ، ربما كان واحدًا من 999,999 استيقاظًا بعد رمي العملة على وجه الكتابة. بمعنى آخر، الإجابة الصحيحة في هذه الحالة هي 1 من كل مليون.
لتقديم امتداد آخر، ماذا لو طُلب من SB توقع نتيجة رمي العملة عند كل استيقاظ؟ إذا كانت صحيحة، فستربح 1000 دولار. إذا كانت لديها استراتيجية لتوقع "الوجه"، فمن المتوقع أن تربح (1/2) × 1000 دولار = 500 دولار. إذا كانت لديها استراتيجية لتوقع "الظهر"، فمن المتوقع أن تربح (1/2) × 2000 دولار = 1000 دولار. إذًا، مجرد استيقاظ SB يُرجّح أن تستقر العملة على الوجه الآخر.
إذا لم يكن شرحي واضحًا، فإن مشكلة الجميلة النائمة على ويكيبيديا تتعمق في الأمر أكثر مما أفعل، بما في ذلك ردود أخرى محتملة من SB.
تم طرح هذا السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .


