اسأل الساحر #405
x 2 - 3 = sqrt(x+3). حل المعادلة لإيجاد قيمة x.
ليكن y = كلا التعبيرين. إذًا، لدينا:
- ص = س^2 - 3
- y = الجذر التربيعي(x+3)
لاحظ الرقم 3 في كلا التعبيرين. لنكتب المعادلتين بـ 3 في أحد طرفيها. أولًا، لدينا:
3 = x^2 - y
الآن، دعونا نقوم بتربيع المعادلة الثانية أعلاه:
y^2 = x+3
3 = y^2 - x
دعونا نساوي بين التعبيرين لـ 3:
x^2 - y = y^2 - x
دعونا نعيد ترتيب الأمر:
x^2 - y^2 + x - y = 0
(x+y)(xy) + x - y = 0
(xy)(x+y+1) = 0
أولاً دعونا نفحص xy = 0:
س ص = 0
فلنستبدل y = x^2 - 3 بـ y.
x - (x^2 - 3) = 0
x^2 - x - 3 = 0
باستخدام صيغة فيثاغورس:
x = (1 +/- الجذر التربيعي (1 + 12) / 2
x = (1 + الجذر التربيعي(13)/2 & x = (1 - الجذر التربيعي(13)/2
ثانيًا، دعونا نفحص x+y+1 = 0:
فلنستبدل y = x^2 - 3 بـ y.
x + (x^2 - 3) + 1 = 0
س + س^2 - 3 + 1 = 0
x^2 + x - 2 = 0
باستخدام صيغة فيثاغورس:
x = (-1 +/- الجذر التربيعي (1 + 8) / 2
x = (-1 +/- 3)/2
x = 1، x = -2
لذا، إجاباتنا الأربعة هي:
- س = 1
- س = -2
- x = (1 + الجذر التربيعي(13)/2 =~ 2.302776
- x = (1 - الجذر التربيعي(13)/2 =~ -1.302776
أود أن أشكر فيديو يوتيوب "حل x^2-3=sqrt(x+3)" من SyberMath على هذه الطريقة لحل هذه المسألة. انتقل إلى الدقيقة 6:28 لمعرفة هذه الطريقة.
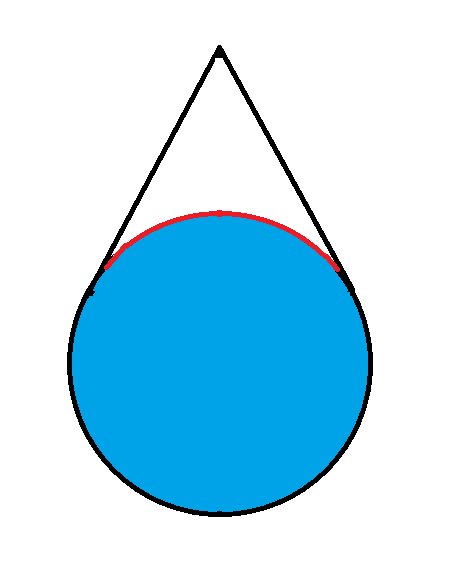
نقطة خارج دائرة نصف قطرها ١ تستطيع رؤية ثلث محيطها. ما بُعد هذه النقطة؟
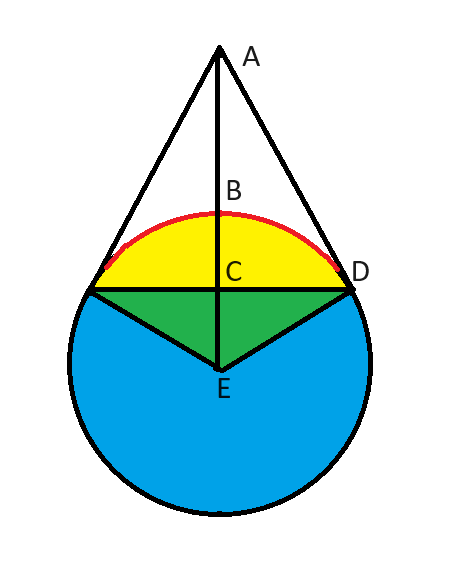
لنأخذ المثلث ADE. نعلم أن:
- الزاوية ADE هي 90 درجة، لأن AD مماس للدائرة.
- زاوية AED هي 60 درجة، لأن زاوية المثلث الأخضر في E هي 120 درجة (1/3 من 360 درجة كاملة).
- يجب أن تكون الزاوية EAD مساوية للـ 30 درجة الأخرى من المثلث ADE.
هذا هو المثلث الكلاسيكي ذو الأضلاع ٣٠-٦٠-٩٠. يجب أن نعلم جميعًا أن أضلاع هذا المثلث متناسبة مع ١، ٢، و الجذر التربيعي (٣).
في هذه الحالة، ED = 1، كما هو موضح في السؤال. AE ضعف هذه المسافة، أي 2.
٢ هو المسافة من النقطة إلى مركز الدائرة. المطلوب هو المسافة من النقطة إلى أقرب نقطة على الدائرة. لذا نطرح نصف القطر. وبالتالي، يكون الناتج ٢-١ = ١.
كان بوب وتوم يسيران عبر جسر قطار، وكانا على بُعد ثلث المسافة من نقطة انطلاقك. ثم سمعا قطارًا قادمًا من خلفهما. كلاهما يركض بسرعة 8 كيلومترات في الساعة. استدار بوب وركض توم للأمام. فاتهما القطار بأقل من ثانية. ما مدى سرعة القطار؟
تذكر أن المسافة = المعدل * الزمن، والذي سنعبر عنه بـ d = r*t
أعد كتابة ذلك: t = d/r.
الوقت هو نفسه في كل من بوب واجتماع القطار في بداية الجسر:
دعونا نترك:
- x = المسافة بين القطار في البداية وبداية الجسر.
- r = معدل سرعة القطار
أولاً، لننظر إلى بوب الذي ركض عائداً. لنكتب t للقاء بوب والقطار في بداية الجسر:
بوب: ت = (1/3)/5
القطار: t = x/r
معادلة التعبيرين لـ t:
(1/3)/5 = x/rr/3 = 5x
ر = 15س
ثانيًا، لننظر إلى توم الذي يركض للأمام. لنكتب حرف (t) لكلٍّ من توم والقطار ليلتقيا في بداية الجسر:
توم: t = (2/3)/5
القطار: t = (1+x)/r
معادلة التعبيرين لـ t:
(2/3)/5 = (1+x)/r
2ر/3 = 5(1+س)
2ر = 15(1+س)
2ر = 15 + 15س
في هذه المرحلة لدينا:
- ر = 15س
- 2ر = 15 + 15س
دعونا نستبدل تعبير r في المعادلة الأولى في المعادلة الثانية:
30x = 15 + 15x
15س = 15
س = 1
تذكر أن r = 15x.
وبالتالي فإن سرعة القطار هي 15*1 = 15 ميلا في الساعة.


