اسأل الساحر #410

أرى أنك أجبتَ على سؤال حول لعبة بلينكو في عمود "السعر مناسب" رقم ١١٥. مع ذلك، يُغيّرون أحيانًا مبالغ الجوائز في العروض الخاصة. على سبيل المثال، في أسبوع المكافآت الكبيرة، كانت الجوائز من اليسار إلى اليمين: ٥٠٠ دولار، ١٠٠٠ دولار، ٢٥٠٠ دولار، ٠ دولار، ٢٠٠٠٠٠ دولار، ٠ دولار، ٢٥٠٠ دولار، ١٠٠٠ دولار، ٥٠٠ دولار. ما القيمة المتوقعة لكل موضع يسقط منه القرص؟ ما احتمالية سقوط القرص في أي جائزة معينة في أي موضع بداية؟

مجهول

هناك تسعة مواضع بداية لإسقاط القرص. مع ذلك، علينا التركيز على خمسة منها فقط لأن الجوائز وترتيب الأوتاد متماثلان. لنُسمِّها، بدءًا من الحافة اليسرى، من ١ إلى ٥.

هناك أيضًا تسعة مواضع نهائية، فلنقم بتسمية الخمسة الأولى منها، بدءًا من اليسار، من 1 إلى 5 أيضًا.

يوضح الجدول التالي احتمالية الهبوط في أي مكان معين (العمود الأيسر) وفقًا للموضع الذي تم إسقاطه منه (الصف العلوي).

نقطة الهبوط	إسقاط 1 أو 9	إسقاط 2 أو 8	إسقاط 3 أو 7	إسقاط 4 أو 6	إسقاط 5
1 أو 9	0.225586	0.193359	0.121094	0.056641	0.032227
2 أو 8	0.386719	0.346680	0.250000	0.153320	0.113281
3 أو 7	0.242188	0.250000	0.257813	0.250000	0.242188
4 أو 6	0.113281	0.153320	0.250000	0.346680	0.386719
5	0.032227	0.056641	0.121094	0.193359	0.225586
المجموع	1.000000	1.000000	1.000000	1.000000	1.000000

يوضح الجدول التالي القيمة المتوقعة لكل مركز إسقاط في أسبوع الجوائز الكبرى الذي سألت عنه. وكما هو متوقع، يجب على اللاعب إسقاط القرص في اتجاه الجائزة الكبرى.

موقع الإنزال	الفوز المتوقع
1 أو 9	7,550.29 دولارًا
2 أو 8	12,396.48 دولارًا
3 أو 7	25,173.83 دولارًا
4 أو 6	39,478.52 دولارًا
5	45,852.05 دولارًا

ما هي مفارقة قرن جبرائيل؟

مجهول

أولاً، لننظر إلى المنحنى من المعادلة y=1/x لقيم x من 1 إلى ما لا نهاية. سيبدو هذا الرسم البياني كما يلي للقيم من x إلى 17.

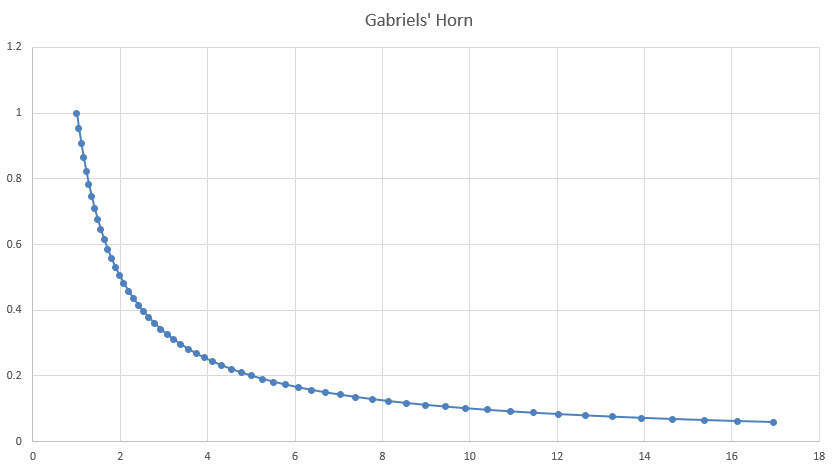
تخيّل بعد ذلك أن هذا المنحنى يدور حول المحور السيني. سيُشكّل ما يشبه القرن، بطرفٍ طويلٍ بلا حدود. هل هذا ما يُطلق عليه علماء الرياضيات قرن جبرائيل؟

المصدر الصورة: روح الرياضيات .

بعد ذلك، فكر في الأسئلة المتعلقة بقرن جبرائيل:

ما هو الحجم؟
ما هي مساحة السطح؟

وهنا الإجابات:

[spoiler=إجابة]

الحجم = π = باي.
مساحة السطح = ما لا نهاية

[/كابح]

يمكنك العثور على أعمالي التي تظهر هذه الإجابات هنا (PDF).

طبيعة المفارقة تسأل كيف يمكن أن يكون الحجم محدودًا بينما تكون مساحة السطح غير محدودة؟

يحدث التناقض المُدرَك عندما نخلط بين بُعدين وثلاثة أبعاد. لا ينبغي لنا فعل ذلك. تخيّل الدائرة أ بنصف قطرها 1، والدائرة ب بنصف قطرها 1.1، حيث تقع الدائرة أ داخل الدائرة ب.

محيط الدائرة أ هو ٢ × ط = ٦٫٢٨٣١٨٥، ومساحة الدائرة ب هي ١٫١^٢ × ط = ٣٫٨٠١٣٢٧. لاحظ أن الدائرة ب أكبر من الدائرة أ، إلا أن مساحتها أقل من محيط الدائرة ب. هذا لا يعني أن محيط الدائرة ب جزء من مساحة الدائرة أ. المساحة والمحيط قياسان مختلفان في أبعاد مختلفة، ولا يجب مقارنتهما.

هناك طريقة أخرى للنظر إلى الأمر وهي إذا صنعنا سجلاً من الدائرة A مع عدد لا نهائي من الأخاديد، فإن طول تلك الأخاديد سيكون لانهائيًا.

بالعودة إلى قرن جبرائيل، فكر في تبسيطه إلى الحالة المنفصلة للدوائر ذات نصف القطر 1، 1/2، 1/3، 1/4 ...

مجموع أحجام هذه الدوائر هو ط*(1/1 + 1/4 + 1/9 + 1/16 + ...). هناك سلسلة لا نهائية معروفة تقول:

1/1 + 1/4 + 1/9 + 1/16 + ... = باي^2/6 =~ 1.644934.

وبإضافة حد باي آخر، يصبح مجموع مساحات الدوائر هو باي^3/6 =~ 5.167713.

في هذه الأثناء، مجموع المحيطات هو 2*pi(1/1 + 1/2 + 1/3 + 1/4 + ...).

هناك سلسلة لا نهائية أخرى معروفة في الرياضيات تسمى السلسلة التوافقية والتي تقول:

1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = ما لا نهاية.

2*pi*∞ لا يزال يساوي ∞.

إذا قمنا بتوسيع هذا المنطق إلى مسافات صغيرة لا نهائية بين الدوائر، فسوف نحصل على قرن جبرائيل.

اشترى ناثان 100 رطل من الفاصوليا. تتكون الفاصوليا من 99% ماء من حيث الوزن. تركها في الشمس لتجف. في اليوم التالي، وجد أنها تتكون من 98% ماء. ما هو وزنها الجديد؟

مجهول

50 رطلاً

[spoiler=الحل]

يترك: