اسأل الساحر #417
أعلم أنك كنت خبيرًا اكتواريًا حكوميًا. مع ذلك، هل الأرقام الواردة في هذا الجدول، والتي يُزعم أنها تُظهر الرسوم الجمركية المفروضة على الواردات إلى الولايات المتحدة وصادرات المنتجات الأمريكية، دقيقة؟

لا.
كنتُ مهتمًا بمصدر هذه الإحصاءات. بدايةً، وجدتُ أن عمود الرسوم الجمركية المفروضة على الولايات المتحدة لا يتعلق بالرسوم الجمركية إطلاقًا، بل بالعجز التجاري. يوضح الجدول التالي قيمة الواردات والصادرات إلى الولايات المتحدة من الدول العشر الأولى في القائمة عام ٢٠٢٤. عمود "نسبة العجز التجاري" هو نسبة الواردات مطروحًا منها الصادرات إلى الواردات. تُعرض الواردات والصادرات بملايين الدولارات. تجدر الإشارة إلى أن هذا العمود يتوافق تمامًا مع الأرقام الواردة في الجدول الذي كان ترامب يحتفظ به.
| دولة | صادرات | الواردات | تجارة العجز نسبة | "التعريفات الجمركية مشحونة "إلى الولايات المتحدة الأمريكية" |
|---|---|---|---|---|
| الصين | 143,546 دولارًا | 438,947 دولارًا | 67% | 67% |
| الاتحاد الأوروبي | 370,189 دولارًا | 605,760 دولارًا | 39% | 39% |
| فيتنام | 13,098 دولارًا | 136,561 دولارًا | 90% | 90% |
| تايوان | 42,337 دولارًا | 116,264 دولارًا | 64% | 64% |
| اليابان | 79,741 دولارًا | 148,209 دولارًا | 46% | 46% |
| الهند | 41,753 دولارًا | 87,416 دولارًا | 52% | 52% |
| كوريا الجنوبية | 65,542 دولارًا | 131,549 دولارًا | 50% | 50% |
| تايلاند | 17,719 دولارًا | 63,328 دولارًا | 72% | 72% |
| سويسرا | 24,962 دولارًا | 63,425 دولارًا | 61% | 61% |
| أندونيسيا | 10,202 دولارًا | 28,085 دولارًا | 64% | 64% |
مصدر الواردات والصادرات: مكتب الإحصاء الأمريكي .
وبالتالي، فإن عمود "الرسوم الجمركية المفروضة على الولايات المتحدة" في الرسم البياني الذي قدمه الرئيس لا علاقة له بالرسوم الجمركية، بل يتعلق ببساطة بعجز الميزان التجاري كنسبة مئوية من الواردات.
قد تتساءل: "ماذا عن العمود الذهبي في عمود "الرسوم الجمركية المتبادلة المخفضة للولايات المتحدة الأمريكية"؟". هذا ببساطة هو الأكبر من نصف عمود "الرسوم الجمركية المفروضة" و10%. يمكن ملاحظة ذلك بمجرد النظر إلى الجدول.
هذا يُظهر ببساطة أن مجرد إلقاء أحدهم الكثير من الأرقام والإحصائيات عليك لا يعني بالضرورة صدقه. في الواقع، إنها طريقة شائعة لخداع الناس بإغراقهم بالأرقام كما لو كانوا يُغرقونهم بخرطوم حريق، على أمل أن يكون المستمع كسولًا جدًا للتحقق منها. لم أرَ مثل هذا الاستغلال الصارخ للإحصائيات منذ أن شاهدتُ هذا الفيديو حول مناظرة الإنسان ضد الدب . في الواقع، جدول "التعريفات المتبادلة" هذا أسوأ.
لنفترض أنني راهنت بمبلغ 100 دولار في لعبة بلاك جاك بلا حدود، وحصلت على زوج من ورقتين مقابل موزع بثلاثة. يُسمح بمضاعفة الرهان بعد التقسيم، ويحق للاعب إعادة التقسيم بلا حدود. ما هو إجمالي الرهان النهائي المتوقع، بافتراض أنني أعدت التقسيم قدر الإمكان وضاعفت الرهان إذا كان مجموع ورقتين من 9 إلى 11؟
لنحسب أولًا عدد الأيدي التي نتوقع إعادة تقسيمها. ليكن n هو عدد الأيدي التي ستنتجها بطاقة واحدة بعد إعادة التقسيم.
ن=(12/13)×1 + (1/13)×2ن
13ن = 12 + 2ن
11ن = 12
ن = 12/11 =~ 1.090909...
مع وجود اثنين من اللاعبين الأساسيين، يمكن للاعب أن يتوقع إعادة التقسيم إلى 2×(12/11) = 24/11 =~ 2.181818 يد.
احتمال سحب 7 مقابل 9 لأي مجموعتين هو 3×(1/12) = 3/12 = 1/4. نقسم على 12 وليس 13، لأنه إذا سحب اللاعب 2، فسيعيد تقسيم الزوج. لذا، فإن متوسط وحدات الرهان لكل يد بعد إعادة التقسيم هو (3/4)×1 + (1/4)×2 = 5/4 = 1.25.
مع رهان أساسي بقيمة 100 دولار، يكون متوسط الرهان النهائي 100 دولار × (24/11) × (5/4) = 272.73 دولار.
تم طرح هذا السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .
افترض أن لاعبين يرغبان في لعب الروليت الروسي وفقًا للقواعد التالية.
- المسدس هو مسدس ذو ستة غرف.
- يجب وضع من رصاصة واحدة إلى خمس رصاصات في الحجرات عند كل سحب للزناد.
- من الممكن أن يتغير عدد الرصاصات الموجودة في البندقية قبل كل سحب.
- يجب أن تتحرك البندقية ذهابًا وإيابًا بعد كل سحب.
- لا يجوز استخدام أي طرق عشوائية أخرى غير البندقية.
ما هي الطريقة التي نضمن من خلالها أن كل لاعب لديه فرصة 50% للبقاء على قيد الحياة؟
هذا مجرد جوابي. أنا متأكد أن هناك آخرين.
- ضع رصاصتين في مسدس اللاعب الأول. إذا نجا، انتقل إلى الخطوة الثانية.
- ضع ثلاث رصاصات في البندقية للاعب الثاني. إذا نجا، ارجع إلى الخطوة ١.
إذا جعلنا p هو احتمال خسارة اللاعب 1، فيمكن حساب ذلك على النحو التالي:
ص = (2/6) + (4/6)*(3/6)ص
36 بنسًا = 12 + 12 بنسًا
24 بنسًا = 12
ص = 12/24 = 1/2
افترض أن أضلاع مربع طول ضلعه أ ممتدة على خط أسفل المربع، مما ينشئ مسافتين 2 و5 على الخط.
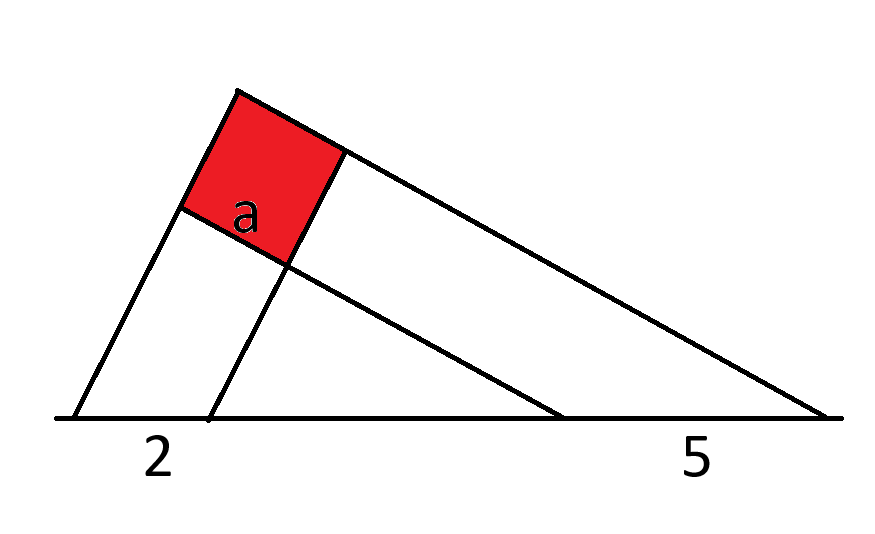
ما هي مساحة المربع؟
أولاً، لنرفع الخط لأعلى حتى يلامس زاوية المربع. هذا لن يؤثر على المسافات على الخط. ثم، لنسمِّ الأضلاع المجهولة للمثلثين.
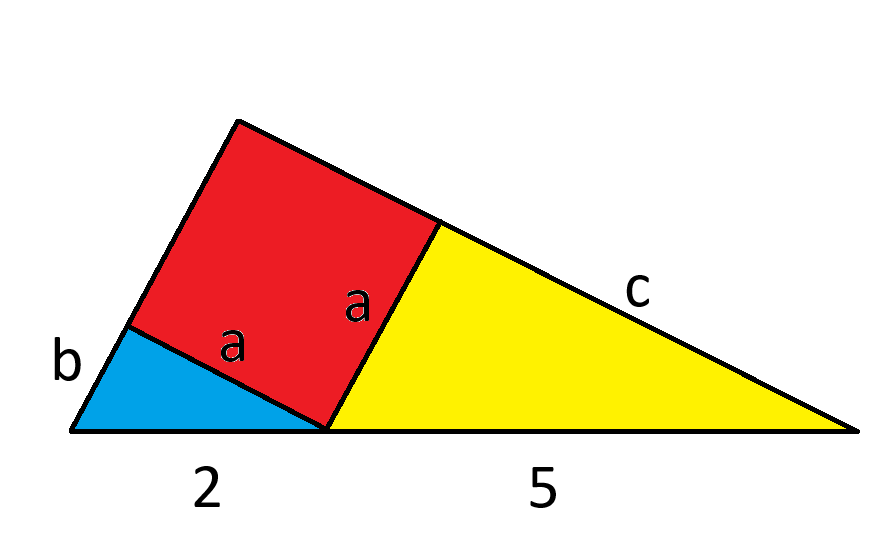
المثلثات الزرقاء والصفراء هي مثلثات قائمة.
باستخدام صيغة فيثاغورس على المثلث الأزرق:
ب 2 + أ 2 = 4
ب = الجذر التربيعي (4-أ 2 )
باستخدام صيغة فيثاغورس على المثلث الأصفر:
ج 2 + أ 2 = 25
ج = الجذر التربيعي(25-أ 2 )
المثلثان الأزرق والأصفر متشابهان. وبالتالي، فإن نسبة أ إلى ب تساوي نسبة ج إلى أ:
أ/الجذر التربيعي(4-أ 2 ) = الجذر التربيعي(25-أ 2 )/أ
أ 2 = الجذر التربيعي (4-أ 2 ) * الجذر التربيعي (25-أ 2 )
تربيع كلا الجانبين:
أ 4 = (4 - أ 2 ) * (25 - أ 2 )
ليكن x = a 2
x 2 = (4-x)(25-x)
x 2 = 100 - 29x + x 2
29س = 100
x = 100/29
أ = الجذر التربيعي(س) = الجذر التربيعي(100/29)
السؤال يطلب مساحة المربع الأحمر، وهي 2 = (sqrt(100/29)) 2 = 100/29.


