<p style=";text-align:right;direction:rtl">مهمتك هي قطع المثلث أدناه إلى قطعتين متساويتين في المساحة بقطع رأسي واحد (أي موازٍ للضلع أ). أين يجب أن يكون القطع؟ </p><p style=";text-align:right;direction:rtl"></p><img alt="" height="354" src="/media/content_images/1610/ask-the-wizard-425-q.png" width="600" />

يجب إجراء القطع ب/الجذر التربيعي (٢) من أقصى يمين المثلث. لاحظ أن الارتفاع لا يهم.<p style=";text-align:right;direction:rtl"></p><p style=";text-align:right;direction:rtl"> وهنا <a href="/pdf/2083/ask-the-wizard-425.pdf">الحل</a> الخاص بي (PDF).</p><p style=";text-align:right;direction:rtl"> تم طرح هذا السؤال ومناقشته في منتدياتي في <a href="https://wizardofvegas.com/forum/questions-and-answers/math/34502-easy-math-puzzles/104/#post964901" target="_blank">Wizard of Vegas</a> .</p>

<p style=";text-align:right;direction:rtl">في <a href="wizardofodds.com/ask-the-wizard/424/">سؤال "اسأل الساحر" رقم 424،</a> سأل أحدهم: "قطعت عصا طولها متر واحد في مكانين عشوائيين. ما المساحة المتوقعة لأصغر قطعة من القطع الثلاث؟" سؤالي هو: ما إجابة عدد القطع العشوائية؟</p>

<div><button onclick='var btn = this; var div = btn.parentNode.childNodes[1]; if (div.style.display != "block") { div.style.display="block"; } else { div.style.display="none"; }' style='padding:2px 4px;'>إجابة</button><div class='spoiler'>1/(c+1)^2</div></div><p style=";text-align:right;direction:rtl"></p><p style=";text-align:right;direction:rtl"> وهنا <a href="/pdf/2082/ask-the-wizard-425b.pdf">الحل الخاص بي</a> (PDF).</p><p style=";text-align:right;direction:rtl"> تم طرح هذه المشكلة ومناقشتها في المنتدى الخاص بي في <a href="https://wizardofvegas.com/forum/questions-and-answers/math/34502-easy-math-puzzles/104/" target=_blank>Wizard of Vegas</a> .</p>

يوصي المعالج

$مكافأة ترحيبية بقيمة 11000

يلعب
مكافأة ترحيبية 100%

يلعب
$مكافأة ترحيبية بقيمة 3000

يلعب
اقرأ المراجعة

بيت ›
اسأل الساحر ›
اسأل الساحر #425

اسأل الساحر #425

مهمتك هي قطع المثلث أدناه إلى قطعتين متساويتين في المساحة بقطع رأسي واحد (أي موازٍ للضلع أ). أين يجب أن يكون القطع؟

مجهول

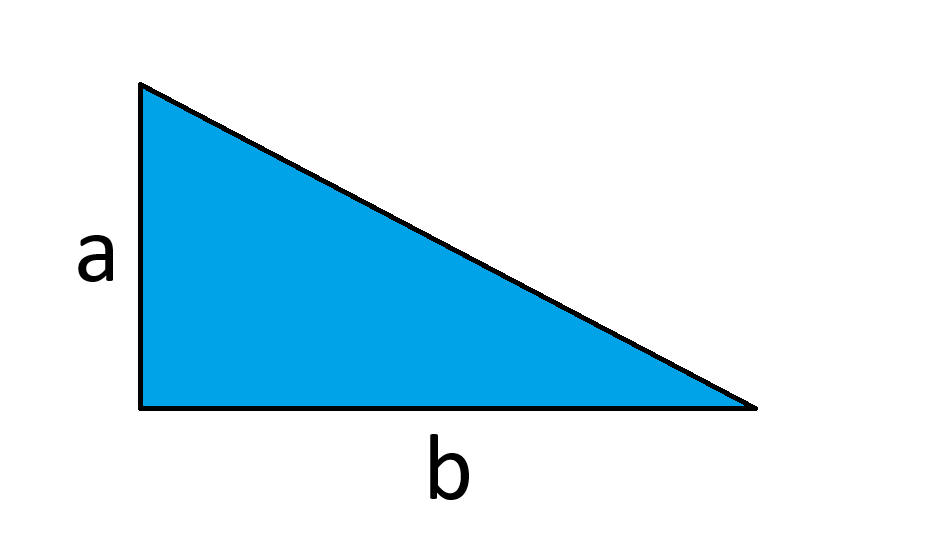
يجب إجراء القطع ب/الجذر التربيعي (٢) من أقصى يمين المثلث. لاحظ أن الارتفاع لا يهم.

وهنا الحل الخاص بي (PDF).

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

في سؤال "اسأل الساحر" رقم 424، سأل أحدهم: "قطعت عصا طولها متر واحد في مكانين عشوائيين. ما المساحة المتوقعة لأصغر قطعة من القطع الثلاث؟" سؤالي هو: ما إجابة عدد القطع العشوائية؟

مجهول

1/(c+1)^2

وهنا الحل الخاص بي (PDF).

تم طرح هذه المشكلة ومناقشتها في المنتدى الخاص بي في Wizard of Vegas .

كم عدد الطرق التي يمكنك بها وضع ست كرات مختلفة في ثلاث صناديق متطابقة؟

مجهول

الجواب هو 122

الجزء الصعب في هذه المسألة هو أن الصناديق متطابقة. لو كانت مختلفة، لكان الحل سهلاً: ٣ ^{× ٦} = ٧٢٩.

دعونا نطلق على الكرات أسماء من A إلى F. نبدأ بوضع الكرة A في أي صندوق.

أولاً، لنفترض أنك وضعت الكرة (ب) في أحد الصندوقين الفارغين المتبقيين. من هنا، تختلف الصناديق الثلاثة لاحتوائها على كرات مختلفة، بما في ذلك كرة لا تزال فارغة. عدد طرق وضع الكرات الأربع الأخرى هو 3 ⁴ = 81.

ثانيًا، لنفترض أنك وضعت الكرة ب في نفس الصندوق مع الكرة أ، والكرة ج في أحد الصندوقين الفارغين. من هنا، تختلف الصناديق الثلاثة لاحتوائها على كرات مختلفة، بما في ذلك كرة فارغة. عدد طرق وضع الكرات الثلاث الأخرى هو ³ = 27.

ثالثًا، لنفترض أنك وضعت الكرتين B وC في نفس الصندوق، بينما وضعت الكرتين A وD في أحد الصندوقين الفارغين. من هنا، تختلف الصناديق الثلاثة لاحتوائها على كرات مختلفة، بما في ذلك كرة فارغة. عدد طرق وضع الكرتين الأخريين هو 3 ² = 9.

رابعًا، لنفترض أنك وضعت الكرات B وC وD في نفس الصندوق، بينما وضعت الكرتين A وE في أحد الصندوقين الفارغين. من هنا، تختلف الصناديق الثلاثة لاحتوائها على كرات مختلفة، بما في ذلك كرة فارغة. عدد طرق وضع الكرة الأخرى هو 3 ^{= 1} = 3.

خامسًا، لنفترض أنك وضعت الكرات من B إلى E في نفس الصندوق، والكرة A والكرة F في أحد الصندوقين الفارغين. لم يتبقَّ أيُّ كرات، لذا هناك طريقة واحدة فقط لوضع الكرتين AE في صندوق وF في صندوق آخر.

سادساً وأخيراً، هناك طريقة واحدة فقط لجميع الكرات الموجودة في نفس الصندوق.

إذن الإجابة هي 3 ⁴ + 3 ³ + 3 ² + 3 ¹ + 2 = 122.

[/كابح]

تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

ما هو متوسط المجموع النهائي للموزع في لعبة البلاك جاك، على افتراض أن الموزع لا يحصل على بلاك جاك ولا يخسر؟

مجهول