اسأل الساحر #426
لنفترض أن الأرقام التسلسلية مُرقّمة تسلسليًا بدءًا من 1. العدد الأقصى المتداول غير معروف. بأخذ عينة عشوائية من n رقم، ما أفضل تقدير للعدد الأقصى؟
أفضل طريقة لحل هذه المسألة هي إيجاد متوسط الفجوة بين الأرقام التسلسلية. ويتم حساب ذلك بقسمة القيمة العظمى على حجم العينة. على سبيل المثال، إذا كان أكبر عنصر في العينة 1000، وكان حجم العينة 5، فإن متوسط المسافة هو 1000/5 = 200. ثم أضف هذه المسافة إلى أقصى عدد مُلاحظ للحصول على أعلى رقم مُقدّر. في هذا المثال، 1000 + 200 = 1200.
الصيغة المُعتادة التي تُعطي نفس العدد هي M*(k+1)/k، حيث M = القيمة العظمى وk = عدد المشاهدات. في مثالنا، يُعطي هذا 1000*(6/5) = 1200.
ABCD هو مربع طول ضلعه 10. يوجد بداخله نصف دائرة وربع دائرة، كما هو موضح في الرسم التخطيطي التالي.
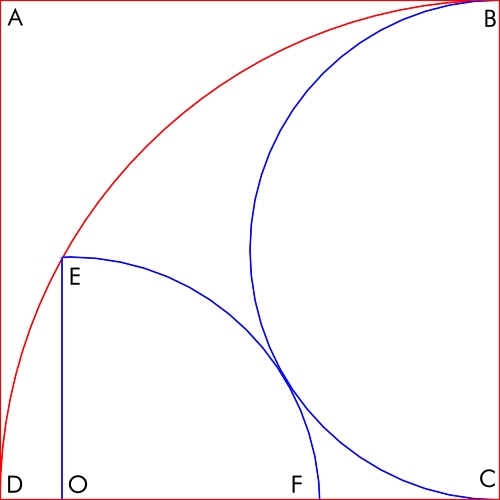
ما هو طول OE؟
انظر إلى الرسم التخطيطي التالي.
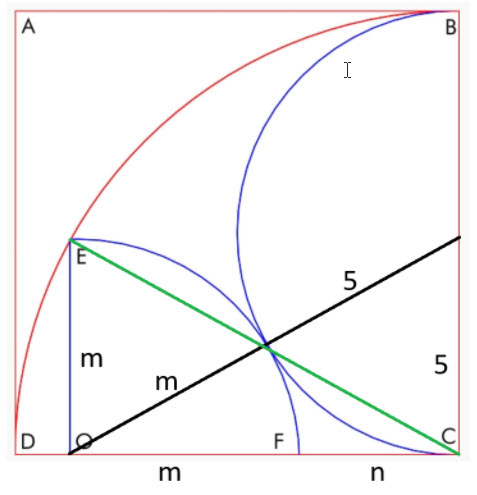
لدينا هنا مثلثان قائمان، أحدهما ذو وتر أخضر والآخر أسود. لنُنشئ معادلتي فيثاغورس:
- الوتر الأخضر: م 2 + (م + ن) 2 = 10 2
- الوتر الأسود: 5 2 + (م+ن) 2 = (م+5) 2
دعونا نعيد ترتيب المعادلة الأولى إلى (م + ن) 2 = 10 2 - م 2
دعونا نعوض تلك القيمة لـ (m+n) 2 في المعادلة الثانية:
5 2 + 10 2 - م 2 = (م + 5) 2
25 + 100 - م 2 = م 2 + 10 م + 25
2م 2 + 10م - 100 = 0
م 2 + 5م - 50 = 0
باستخدام صيغة فيثاغورس لحل m:
م = (-5 +/- الجذر التربيعي (25 + 200))/2
م = 5 أو -10. 5 هي الإجابة المعقولة الوحيدة.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يخضع عدد كبير من الطلاب لاختبار مكون من عشرة أسئلة. جميع الأسئلة إما صحيحة أو خاطئة. ما هو الحد الأقصى لعدد الطلاب المسموح به للاختبار بحيث يختلف أي اختبارين عن بعضهما بسؤالين على الأقل؟
قم بإجراء اختبار واحد والذي سنطلق عليه الاختبار الرئيسي.
المجموعة 1 = عدد الطرق التي يمكن أن تختلف بها الاختبارات الأخرى عن الاختبار الرئيسي بسؤالين بالضبط هو combin(10,2)=45.
لن أقوم بحساب عدد الطرق التي يجب أن تكون مختلفة بمقدار 3 عن الاختبار الرئيسي، لأن بعض هذه الطرق سوف تطابق 9 من 10 لاختبار من المجموعة 1.
المجموعة ٢ = عدد الطرق التي يمكن أن تختلف بها الاختبارات الأخرى عن الاختبار الرئيسي بأربعة أسئلة بالضبط هو combin(10,4)=210. أيٌّ منها سيختلف أيضًا عن أي اختبار في المجموعة ١ بفارق سؤالين على الأقل.
تكرار هذا المنطق...
- المجموعة 3 = عدد الطرق التي يمكن أن تختلف بها الاختبارات الأخرى عن الاختبار الرئيسي بـ 6 أسئلة بالضبط هو combin(10,6)=210.
- المجموعة 4 = عدد الطرق التي يمكن أن تختلف بها الاختبارات الأخرى عن الاختبار الرئيسي بـ 8 أسئلة بالضبط هو combin(10,8)=45.
- المجموعة 5 = عدد الطرق التي يمكن أن تختلف بها الاختبارات الأخرى عن الاختبار الرئيسي بـ 10 أسئلة بالضبط هو combin(10,10)=1.
لذا، فإن الإجابة هي مجموع المجموعات من 1 إلى 5 زائد واحد للاختبار الرئيسي = 1+45+210+210+45+1 = 512.
هذا العدد هو نفسه ٢^٩. هل يمكن أن يكون هذا مصادفة؟ لا!
عدد طرق سحب عدد فردي من العناصر من مجموعات أكبر هو نفسه عدد طرق سحب عدد زوجي. وذلك لأن كل عنصر في المجموعة الكبيرة يمكن سحبه أو عدم سحبه. يوجد 2^n من التركيبات لكل عنصر يتم سحبه أو عدم سحبه في مجموعة من n عنصر. إذا رتبتها بشكل منهجي بترتيب ثنائي، فسيكون عدد التركيبات المختارة متناوبًا بين الزوجي والفردي. العدد الإجمالي للمجموعة هو 2^n، وهو في حد ذاته زوج، لذا سيكون نصف 2^n زوجًا.
إذن، مجموع المجموعات من ١ إلى ٥ هو عدد طرق اختيار عدد زوجي من الأسئلة التي تُطابق الاختبار الرئيسي. وهذا يُعادل عدد طرق اختيار عدد فردي من الأسئلة التي تُطابق الاختبار الرئيسي. إجمالي عدد طرق مطابقة أو عدم مطابقة الاختبار الرئيسي هو ٢^١٠ = ١٠٢٤. نصف هذه الطرق يُطابق عددًا زوجيًا من المرات. إذن، الإجابة هي ١٠٢٤/٢ = ٥١٢.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .


