Q: يتعلق هذا الأمر بالتحكم في النرد في لعبة الكرابس. سبق أن ناقشتَ <a href="/games/craps/appendix/3/">تجربة ستانفورد وونغ</a> ، وقلتَ: &quot;كانت شروط الرهان هي ما إذا كان بإمكان الرماة الدقيقين رمي أقل من 79.5 رقم سبعة في 500 رمية. العدد المتوقع في لعبة عشوائية هو 83.33. احتمال رمي 79 رقم سبعة أو أقل في 500 رمية عشوائية هو 32.66%... واحتمال رمي 74 رقم سبعة أو أقل في 500 رمية عشوائية هو 14.41%.&quot; السؤال الذي لدي بخصوص هذا الرهان هو أن 14.41% لا يزال غير &quot;ذو دلالة إحصائية&quot; [أي p &lt; 0.05]، وهو ما يُفهم عادةً على أنه يعني أكبر من انحرافين معياريين عن المتوسط - أو احتمال أقل من 5% * مجتمعة* من وقوع الحدث عشوائيًا في أي من طرفي السلسلة. كم عدد السبعات التي يجب أن تظهر في 500 لفة قبل أن تتمكن من القول أن هناك فرصة أقل من 2.5٪ أن النتيجة كانت عشوائية تمامًا (أي أن النتيجة كانت ذات دلالة إحصائية)؟ شكرا جزيلا وبالمناسبة، موقعك هو أفضل موقع على الإطلاق فيما يتعلق بموضوع احتمالات وفرص المقامرة التي وجدتها .... استمر في العمل الجيد !!!

شكراً لكلماتك الطيبة. لا يجب أن تُصرّح بأن احتمالية عدم عشوائية الرميات هي p. بل يجب أن تُصاغ على أن احتمالية أن تُسفر لعبة عشوائية عن مثل هذه النتيجة هي p. لم يتوقع أحد أن تُثبت 500 رمية أي شيء أو تُدحضه. لم أكن أنا من حدد الخط عند 79.5 سبعات، لكنني أشك في أنه تم اختياره ليكون ذا دلالة إحصائية؛ بل أظن أنه كان نقطةً يتفق عندها الطرفان على الرهان. مستوى الدلالة 2.5% يساوي 1.96 انحرافًا معياريًا عن التوقعات. يمكن حساب ذلك باستخدام الصيغة =normsinv(0.025) في برنامج إكسل. الانحراف المعياري لـ 500 رمية هو sqr(500*(1/6)*(5/6)) = 8.333. لذا، فإن 1.96 انحرافًا معياريًا يساوي 1.96 * 8.333 = 16.333 رمية أقل من التوقعات. العدد المتوقع للسبعات في 500 رمية هو 500*(1/6) = 83.333. لذا، فإن 1.96 انحرافًا معياريًا أقل من ذلك يساوي 83.333 − 16.333 = 67. وبالتحقق من ذلك باستخدام التوزيع الثنائي، فإن الاحتمال الدقيق لـ 67 أو أقل من السبعات هو 2.627%.

Q: في الأخبار اليوم، ألقت امرأة في أتلانتيك سيتي 154 مرة متتالية قبل أن تحصل على الرقم سبعة في <a href="http://www.theborgata.com/" target=_blank>بورغاتا</a> . هذا يعني أنها ألقت نردين 154 مرة، دون أي رقم سبعة. لذلك أخذت (30/36) 154 ، وتوصلت إلى احتمالات تزيد عن 1.5 تريليون إلى 1. إن احتمالية فوز المرء في يانصيب ميجا مليونز أكبر بنحو 9000 مرة من إمكانية تحقيق ماراثون رمي نرد بدون الرقم سبعة لمدة 154 مرة متتالية. ونظرًا لمدى احتمالية حدوث ذلك بشكل فلكي، ونظرًا لأن الأشخاص يُدانون بناءً على أدلة الحمض النووي التي تبلغ مليارات إلى واحد فقط مقابل كونها مطابقة خاطئة، فما مدى اشتباهك في الغش، وهل ستعرض استشارة بورغاتا بشأن هذا الأمر؟ لقد اتصلت بهم بالفعل، وأعطيتهم اسمي، وطلبت منهم أن يفعلوا به ما يريدون. أنا فضولي بشأن أفكارك.

أولاً، ألقت النرد ما مجموعه 154 مرة، وكانت اللفة 154 هي سبعة خارج ( <a href=http://www.nj.com/news/index.ssf/2009/05/craps_player_sets_record_roll.html target=_blank>المصدر: NJ.com</a> ). ومع ذلك، هذا لا يعني أنها لم تدرِ سبعة أبدًا في أول 153 لفة. كان بإمكانها أن تدرِج الكثير منها في رميات الخروج. وكما أوضحت في <a href=/ask-the-wizard/81/>عمودي بتاريخ 3 مايو 2003</a> ، فإن احتمال الوصول إلى اللفة 154 هو 1 من 5.6 مليار. واحتمالات الفوز في Mega Millions هي 1 في <a href="/gambling/glossary/#combin">المجموعة</a> (56،5) * 46 = 175،711،536. لذا فإن الحصول على 154 لفة أو أكثر يكون أصعب بحوالي 32 مرة. مع وجود وقت كافٍ وجداول، والتي أعتقد أنها موجودة، كان من المحتم أن يحدث شيء من هذا القبيل عاجلاً أم آجلاً. لذلك، لا أشك في الغش. أقدر تقريبًا احتمال حدوث ذلك في أي عام معين بحوالي 1٪. انظر أيضًا حلي، المعبر عنه بالمصفوفات، على <a href=http://mathproblems.info/ target=_blank>mathproblems.info</a> ، المشكلة 204.

Question 1

كنت أتساءل عن كيفية تغيير النرد في لعبة الكرابس بحيث يظهر 7 أو 11 في كل مرة هل يمكنك مساعدتي. شكرا لك.

Accepted Answer

ثم قم بتغييرها بحيث يكون أحد النردين يحتوي على الرقم ستة على كل جانب، والآخر يحتوي على الرقم واحد والخمسة على كل جانب.

Question 2

هل تعتقد أن &quot;تفكير اللاعبين التفاؤلي&quot; قد يؤثر على نتيجة اللعبة؟ مع العلم أنني لا أهتم بحجم التأثير، بل برأيك الفلسفي فقط. وهل تعتقد أيضًا أن طريقة رمي اللاعب للنرد في لعبة الكرابس قد تُسبب انحيازًا (سواءً كان إيجابيًا أو سلبيًا) في النتيجة؟ موقعك رائع كالعادة.

Accepted Answer

شكراً على كلماتك الطيبة. لا، لا أعتقد أن التفاؤل يُجدي نفعاً في الكازينو، مع تساوي جميع العوامل الأخرى.

مسألة تأثير النرد موضوعٌ مثيرٌ للجدل. أنا شخصياً متشككٌ جداً. فبينما أراجع هذا الرد عام ٢٠١٣، ما زلتُ أبحث عن دليلٍ مقنعٍ على قدرة أي شخصٍ على التأثير بما يكفي ليحظى بأفضلية.

Question 3

أتساءل فقط عن رأيك في تغيير جدول التردد في لعبة الكرابس عن طريق ضبط النرد مسبقًا.

Accepted Answer

أنا متشككٌ جدًا في الأمر. سأستعرض بعض التجارب المتعلقة بهذا الموضوع في ملحق الكرابس رقم 3 .

Question 4

تعرّفتُ مؤخرًا على بعض المعلومات حول استراتيجيات توزيع النرد في لعبة الكرابس. يعتقد البعض أنه يُمكن توزيع النرد بطريقة مُحددة قبل الرمية، وبإبقاء رمي النرد على محور دوران واحد فقط، يُمكن الحصول على عدد أقل من السبعات المُحتملة مع مجموعات نرد مُحددة. أردتُ معرفة مدى صحة هذا أم أنه مُجرد مُغالطة.

Accepted Answer

لا أؤمن بها. حتى الآن، لم أرَ اسمًا أحترمه يُؤيد هذه الطريقة، ولا أي دليل على فعاليتها. مع أنني لا أستبعدها تمامًا، إلا أنني أشك فيها بشدة. قد أعيش في نيفادا، ولكن عندما يتعلق الأمر بأمور مثل وضع النرد، فأنا من ميسوري، &quot;أرني&quot; أنها ناجحة.

Question 5

هل النرد محايد حقًا؟ يبدو أن الجوانب ذات الأرقام الأكبر والثقوب الأكثر ستكون أخف من الجوانب ذات الأرقام الأصغر والثقوب الأقل. هذا يشير إلى أن الجوانب الأثقل ستسقط على الأرجح مقلوبة، بينما ستسقط الأرقام الأكبر مكشوفة. أستطيع أن أتخيل نظام كرابس قد يحاول استغلال هذا المبدأ، لكنني أتساءل إن كان سينجح حقًا. ما رأيك؟

Accepted Answer

ينطبق هذا على النرد العادي، مثل النرد الموجود في ألعاب الطاولة. مع ذلك، تحتوي نردات الكازينو على نقاط مرصعة. في المصنع، يُثقبون ثقوبًا لهذه النقاط، ثم يُدخلون فيها نقاطًا بيضاء اللون، بنفس كثافة النرد نفسه. لذا، يكون النرد في جوهره مكعبًا مثاليًا. حتى لو استخدموا نردًا عاديًا من لعبة طاولة، أشك في أن هذا التحيز سيكون كافيًا للتغلب على هامش الكازينو.

Question 6

هل تعتقد أن رمي النرد على طاولة كازينو كرابس عشوائي حقًا كما هو الحال في مولد الأرقام العشوائية، أم أن هناك رماة جيدين ورماة سيئين إما من خلال &quot;ميكانيكا&quot; النرد أو الرمي غير الدقيق (الرميات القصيرة كمثال)، إذا لم تكن لعبة كرابس الكازينو في العالم الحقيقي عشوائية حقًا، فكيف يمكنني الاستفادة من هذا؟

Accepted Answer

أعتقد أنه لا يوجد رماة سيئون بالفطرة. باستثناء بعض المحترفين، يمكن اعتبار جميع رميات النرد عشوائية تمامًا. تُعقد ندوات حول كيفية التغلب على ميزة الكازينو في لعبة الكرابس عن طريق الرمي الاستباقي، لكنني لا أؤيدها أو أعارضها. لم أجد أدلة كافية على أيٍّ من الأمرين حتى الآن.

Question 7

في عدد أكتوبر من مجلة &quot;كازينو بلاير&quot;، كتب فرانك سكوبليت مقالاً عن رمي النرد المُتحكّم فيه، حيث ذكرتَ أنك خسرتَ 1800 دولار أمام ستانفورد وونغ عندما لم يحصل إلا على 74 رقم سبعة في 500 رمية. لماذا راهنتَ على عينة صغيرة كهذه (500)؟ يجب على الشخص الذي يدّعي قدرته على التحكم بالنرد أن يكون مستعدًا لإثبات مهارته برمي 50,000 رمية على الأقل. هل أنا مخطئٌ في اعتقادي أن 500 رمية عينة صغيرة جدًا لدرجة أن أي شيء تقريبًا قد يحدث؟

Accepted Answer

خسرتُ مبلغ الـ ١٨٠٠ دولار أمريكي أمام كاتب مقامرة آخر، وليس ستانفورد. كنتُ أُفضّل المزيد من الرميات، لكن كان هناك قيد زمني واضح. بافتراض رمية واحدة في الدقيقة، سيستغرق الأمر ٣٤.٧ يومًا لرمي النرد ٥٠ ألف مرة. لم أكن أنا من قرر ٥٠٠، لكن بدا لي حلاً وسطًا معقولًا بين حجم العينة الكبير والوقت. أنت مُحقّ في أن ٥٠٠ عدد قليل جدًا لتكوين حجة قوية لصالح أو ضد التأثير على النرد، لكن ٥٠٠ رمية أفضل من لا شيء.

Question 8

أعلم أنك متشكك في التحكم بالنرد. لقد كنت أتدرب على ضبط النرد والتحكم في الرمي لمدة ثلاثة أشهر. ما هو احتمال ظهور 78 رقمًا سبعةً من أصل 655 رمية عشوائيًا؟ شكرًا لمساعدتك :)

Accepted Answer

بالنسبة لعدد كبير من الرميات، يُمكننا استخدام تقريب منحنى غاوس. العدد المتوقع للسبعات في 655 رمية هو 655 × (1/6) = 109.1667. التباين هو 655 × (1/6) × (5/6) = 90.9722. الانحراف المعياري هو sqr(90.9722) = 9.5379. عدد السبعات الـ 78 لديك أقل من المتوقع بمقدار 109.1667 − 78 = 31.1667. هذا يساوي (31.1667 - 0.5) / 9.5379 = 3.22 انحراف معياري عن المتوقع. احتمالية انخفاض 3.22 انحراف معياري أو أكثر عن المتوقع هي 0.000641، أو 1 من 1560. حصلت على هذا الرقم في Excel، باستخدام الصيغة normsdist(-3.22).

Question 9

يتعلق هذا الأمر بالتحكم في النرد في لعبة الكرابس. سبق أن ناقشتَ تجربة ستانفورد وونغ ، وقلتَ: "كانت شروط الرهان هي ما إذا كان بإمكان الرماة الدقيقين رمي أقل من 79.5 رقم سبعة في 500 رمية. العدد المتوقع في لعبة عشوائية هو 83.33. احتمال رمي 79 رقم سبعة أو أقل في 500 رمية عشوائية هو 32.66%... واحتمال رمي 74 رقم سبعة أو أقل في 500 رمية عشوائية هو 14.41%."

السؤال الذي لدي بخصوص هذا الرهان هو أن 14.41% لا يزال غير "ذو دلالة إحصائية" [أي p < 0.05]، وهو ما يُفهم عادةً على أنه يعني أكبر من انحرافين معياريين عن المتوسط - أو احتمال أقل من 5% * مجتمعة* من وقوع الحدث عشوائيًا في أي من طرفي السلسلة.

كم عدد السبعات التي يجب أن تظهر في 500 لفة قبل أن تتمكن من القول أن هناك فرصة أقل من 2.5٪ أن النتيجة كانت عشوائية تمامًا (أي أن النتيجة كانت ذات دلالة إحصائية)؟

شكرا جزيلا وبالمناسبة، موقعك هو أفضل موقع على الإطلاق فيما يتعلق بموضوع احتمالات وفرص المقامرة التي وجدتها .... استمر في العمل الجيد !!!

Accepted Answer

شكراً لكلماتك الطيبة. لا يجب أن تُصرّح بأن احتمالية عدم عشوائية الرميات هي p. بل يجب أن تُصاغ على أن احتمالية أن تُسفر لعبة عشوائية عن مثل هذه النتيجة هي p. لم يتوقع أحد أن تُثبت 500 رمية أي شيء أو تُدحضه. لم أكن أنا من حدد الخط عند 79.5 سبعات، لكنني أشك في أنه تم اختياره ليكون ذا دلالة إحصائية؛ بل أظن أنه كان نقطةً يتفق عندها الطرفان على الرهان.

مستوى الدلالة 2.5% يساوي 1.96 انحرافًا معياريًا عن التوقعات. يمكن حساب ذلك باستخدام الصيغة =normsinv(0.025) في برنامج إكسل. الانحراف المعياري لـ 500 رمية هو sqr(500*(1/6)*(5/6)) = 8.333. لذا، فإن 1.96 انحرافًا معياريًا يساوي 1.96 * 8.333 = 16.333 رمية أقل من التوقعات. العدد المتوقع للسبعات في 500 رمية هو 500*(1/6) = 83.333. لذا، فإن 1.96 انحرافًا معياريًا أقل من ذلك يساوي 83.333 − 16.333 = 67. وبالتحقق من ذلك باستخدام التوزيع الثنائي، فإن الاحتمال الدقيق لـ 67 أو أقل من السبعات هو 2.627%.

Question 10

قبل ثلاث سنوات، في عمود "اسأل الساحر "، كتبتَ: "أنت محقّ في أن 500 رمية قليلة جدًا لإثبات صحة تأثير النرد أو عدمه، لكن 500 رمية أفضل من لا شيء". هل يمكنك وصف ما تحتاجه من شخص يُزعم أنه مؤثر على النرد، في تجربة، لتشعر بالثقة الكافية للبدء بالمراهنة عليه بمبالغ طائلة؟ أسأل لأن مليار جولة تُعدّ معيارًا جيدًا للنتائج "الموثوقة" في بعض ألعاب محاكاة البلاك جاك. مع التصميم التجريبي الأكثر كفاءة (أي الذي يتطلب أقل عدد من الرميات) الذي يمكنك تخيله، كم عدد الرميات التي يحتاجها اللاعب ليكون واثقًا من تأثيره على النتائج؟ أعلم أن الإجابة ستعتمد على مهارة اللاعب، لكنك تفهم قصدي. إذا كنت بحاجة إلى مليون رمية حتى في أفضل الأحوال، فلن يكون الأمر مجديًا.

Accepted Answer

لا توجد نقطة حاسمة تُكتسب عندها الثقة. إنها مسألة درجة. أولًا، أود أن أسأل عن طبيعة الاختبار، وما يتوقعه مطلق النار. في أي اختبار، هناك خطأان محتملان. قد يفشل مطلق نار ماهر بسبب سوء الحظ، أو قد ينجح مطلق نار عشوائي بسبب حسن الحظ. من بين الاثنين، أُفضّل تجنب النتيجة الإيجابية الخاطئة. أعتقد أن الاختبار المعقول سيُحدد احتمال النتيجة السلبية الخاطئة بحوالي 5%، واحتمال النتيجة الإيجابية الخاطئة بحوالي 1%.

على سبيل المثال، لنفترض أن المُدّعي يقول إنه يستطيع الحصول على متوسط سبعة نقاط كل سبع رميات للنرد. سيُلقي مُقامر عشوائي نقطة واحدة كل ست رميات في المتوسط. بالتجربة والخطأ، أجد أن الاختبار الذي يُلبي هذين المعيارين هو رمي النرد ٣٦٠٠ مرة، ويتطلب ٥٤٧ نقطة أو أقل للنجاح، أو نقطة واحدة لكل ٦.٥٨ رمية.

يُفترض أن يُحرز رامي واحد من كل سبعة رميات 514.3 رمية سباعية، بانحراف معياري قدره 21.00. باستخدام التقريب الغاوسي، فإن احتمال أن يُحرز رامي ماهر 548 رمية سباعية أو أكثر (نتيجة سلبية خاطئة) هو 5.7%. أما الرامي العشوائي، فيُفترض أن يُحرز رمية سباعية في المتوسط 600 رمية، بانحراف معياري قدره 22.36. أما احتمال اجتياز رامي عشوائي للاختبار (نتيجة إيجابية خاطئة) فهو 0.94%. يُظهر الرسم البياني أدناه النتائج المحتملة للرماة المهرة والعشوائيين. إذا كانت النتائج على يسار الخط الأخضر، فسأعتبر الرامي قد اجتاز الاختبار، وسأراهن عليه.

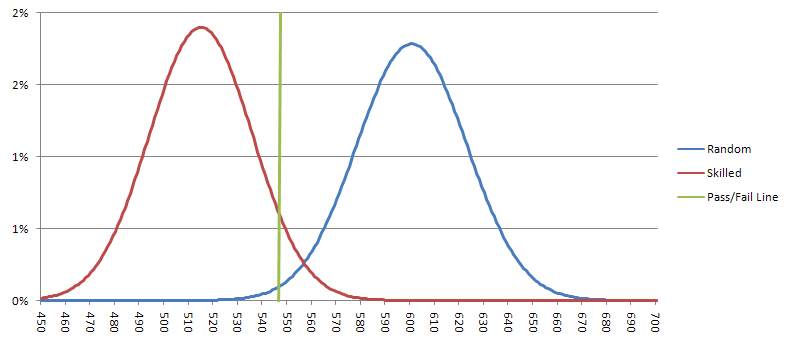
المعضلة العملية هي أنه إذا افترضنا رميتين في الدقيقة، فسيستغرق إجراء الاختبار 30 ساعة. ربما يمكنني أن أكون أكثر مرونة بشأن مستوى الدلالة، لتقليل الوقت المطلوب، لكن النتائج لن تكون بنفس القدر من الإقناع. أعتقد أن الوقت قد حان لاختبار أكبر من تجربة وونغ التي أجريت 500 رمية.

Question 11

في الأخبار اليوم، ألقت امرأة في أتلانتيك سيتي 154 مرة متتالية قبل أن تحصل على الرقم سبعة في بورغاتا . هذا يعني أنها ألقت نردين 154 مرة، دون أي رقم سبعة. لذلك أخذت (30/36) ¹⁵⁴ ، وتوصلت إلى احتمالات تزيد عن 1.5 تريليون إلى 1. إن احتمالية فوز المرء في يانصيب ميجا مليونز أكبر بنحو 9000 مرة من إمكانية تحقيق ماراثون رمي نرد بدون الرقم سبعة لمدة 154 مرة متتالية. ونظرًا لمدى احتمالية حدوث ذلك بشكل فلكي، ونظرًا لأن الأشخاص يُدانون بناءً على أدلة الحمض النووي التي تبلغ مليارات إلى واحد فقط مقابل كونها مطابقة خاطئة، فما مدى اشتباهك في الغش، وهل ستعرض استشارة بورغاتا بشأن هذا الأمر؟ لقد اتصلت بهم بالفعل، وأعطيتهم اسمي، وطلبت منهم أن يفعلوا به ما يريدون. أنا فضولي بشأن أفكارك.

Accepted Answer

أولاً، ألقت النرد ما مجموعه 154 مرة، وكانت اللفة 154 هي سبعة خارج ( المصدر: NJ.com ). ومع ذلك، هذا لا يعني أنها لم تدرِ سبعة أبدًا في أول 153 لفة. كان بإمكانها أن تدرِج الكثير منها في رميات الخروج. وكما أوضحت في عمودي بتاريخ 3 مايو 2003 ، فإن احتمال الوصول إلى اللفة 154 هو 1 من 5.6 مليار. واحتمالات الفوز في Mega Millions هي 1 في المجموعة (56،5) * 46 = 175،711،536. لذا فإن الحصول على 154 لفة أو أكثر يكون أصعب بحوالي 32 مرة. مع وجود وقت كافٍ وجداول، والتي أعتقد أنها موجودة، كان من المحتم أن يحدث شيء من هذا القبيل عاجلاً أم آجلاً. لذلك، لا أشك في الغش. أقدر تقريبًا احتمال حدوث ذلك في أي عام معين بحوالي 1٪.

انظر أيضًا حلي، المعبر عنه بالمصفوفات، على mathproblems.info ، المشكلة 204.

Question 12

أعتقد أن بعض كازينوهات لاس فيغاس تستخدم نردًا مُرجحًا على أحد وجهيه. وكدليل على ذلك، أُقدّم نتائج 244 رمية جمعتها في كازينو ستريب. ما هي احتمالات ظهور هذه النتائج غير المتوازنة من نرد عادل؟

بيانات اختبار النرد
مجموع النرد	الملاحظات
2	6
3	12
4	14
5	18
6	23
7	50
8	36
9	37
10	27
11	14
12	7
المجموع	244

Accepted Answer

7.7%.

اختبار مربع كاي مناسب تمامًا لهذا النوع من الأسئلة. لاستخدامه، احسب (ae) ² / e لكل فئة، حيث a هي النتيجة الفعلية، وe هي النتيجة المتوقعة. على سبيل المثال، العدد المتوقع للرميات بمجموع 2 في 244 رمية هو 244 × (1/36) = 6.777778. إذا كنت لا تفهم لماذا يكون احتمال الحصول على 2 هو 1/36، فيُرجى قراءة صفحتي حول أساسيات احتمالات النرد . بالنسبة لقيمة مربع كاي لمجموع 2، a = 6 وe = 6.777778، لذا (ae) ² / e = (6-6.777778) ² / 6.777778 = 0.089253802.

نتائج مربع كاي

مجموع النرد	الملاحظات	مُتوقع	مربع كاي
2	6	6.777778	0.089253
3	12	13.555556	0.178506
4	14	20.333333	1.972678
5	18	27.111111	3.061931
6	23	33.888889	3.498725
7	50	40.666667	2.142077
8	36	33.888889	0.131512
9	37	27.111111	3.607013
10	27	20.333333	2.185792
11	14	13.555556	0.014572
12	7	6.777778	0.007286
المجموع	244	244	16.889344

ثم احسب مجموع عمود مربع كاي. في هذا المثال، المجموع هو 16.889344. وهذا ما يُسمى إحصائية مربع كاي. عدد "درجات الحرية" أقل بواحد من عدد الفئات في البيانات، في هذه الحالة 11-1 = 10. أخيرًا، ابحث عن إحصائية مربع كاي التي تبلغ 10.52 و10 درجات حرية في جدول إحصائي، أو استخدم الصيغة =chidist(16.889344,10) في برنامج إكسل. سيعطيك أيٌّ منهما نتيجة 7.7%. هذا يعني أن احتمالية أن تُنتج نردًا عادلًا نتائج بهذا الانحراف أو أكثر هي 7.7%. خلاصة القول هي أنه على الرغم من أن هذه النتائج أكثر انحرافًا مما هو متوقع، إلا أنها ليست منحرفة بما يكفي لإثارة الشكوك. إذا تابعت هذا الاختبار، أقترح جمع النتيجة الفردية لكل نرد، بدلاً من المجموع. تجدر الإشارة أيضًا إلى أن اختبار مربع كاي غير مناسب إذا كان العدد المتوقع لنتائج فئة ما منخفضًا. ويُعتبر الحد الأدنى المتوقع وهو 5 أرقامًا شائعة.

Question 13

ماذا سيحدث إذا سقط النردان متراكبين في لعبة الكرابس؟ هل يُعتبر ذلك رميًا صحيحًا؟ إذا كان الأمر كذلك، فكيف سيكشف الموزع عن الرقم الذي سقط عليه النرد السفلي؟

Accepted Answer

يعتمد اعتبارها لفة صحيحة على مكان تواجدك. تنص لائحة ألعاب نيوجيرسي رقم 19:47-1.9(أ) على ما يلي:

"تكون رمية النرد غير صالحة عندما يخرج أحد النردين أو كلاهما من على الطاولة أو عندما يستقر أحد النردين فوق الآخر." -- نيوجيرسي 19: 47-1.9 (أ)

ولاية بنسلفانيا لديها نفس اللائحة بالضبط، القسم 537.9 (أ) :

تصبح رمية النرد غير صالحة عندما يخرج أحد النردين أو كلاهما من على الطاولة أو عندما يستقر أحد النردين فوق الآخر. -- PA 537.9(a)

سألتُ موزع نرد من لاس فيغاس، فأجابني بأنه في هذه الحالة، تُعتبر رمية صحيحة، لو كانت رمية صحيحة. مع أنه لم يرَ ذلك يحدث قط، إلا أنه قال إنه لو حدث، لكان الموزعون ببساطة سيحركون النرد العلوي لمعرفة الرقم الذي استقر عليه النرد السفلي. مع ذلك، يُمكن تحديد نتيجة النرد السفلي دون لمس النرد العلوي أو النظر من خلاله. إليك كيفية القيام بذلك: أولًا، بالنظر إلى الجوانب الأربعة، يُمكنك تضييق الاحتمالات في الأعلى إلى اثنين. إليك كيفية تحديد الاحتمالات الثلاثة بناءً على ذلك.

١ أو ٦: ابحث عن الرقم ٣. إذا كانت النقطة العليا تُحدّ الرقم ٥، فالرقم ١ في الأعلى. أما إذا كانت تُحدّ الرقم ٢، فالرقم ٦ في الأعلى.
٢ أو ٥: ابحث عن الرقم ٣. إذا كانت النقطة العليا تُحدّ الرقم ٦، فالرقم ٢ في الأعلى. أما إذا كانت تُحدّ الرقم ١، فالرقم ٥ في الأعلى.
٣ أو ٤: ابحث عن الرقم ٢. إذا كانت النقطة العليا تُحدّ الرقم ٦، فالرقم ٣ في الأعلى. أما إذا كانت تُحدّ الرقم ١، فالرقم ٤ في الأعلى.

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

Question 14

ما هو العدد المتوقع لرميات النردين لكل مجموع من 2 إلى 12 ليحدث مرة واحدة على الأقل؟

Accepted Answer

طُرح هذا السؤال على موقع TwoPlusTwo.com، وأجاب عليه BruceZ بشكل صحيح. الحل التالي هو نفس طريقة BruceZ، الذي يستحق التقدير. الإجابة صعبة، لذا انتبه.

أولاً، خُذ في الاعتبار العدد المتوقع للرميات للحصول على مجموع اثنين. احتمال الحصول على اثنين هو ١/٣٦، لذا يتطلب الأمر ٣٦ رمية في المتوسط للحصول على أول اثنين.
بعد ذلك، لنفترض عدد الرميات المتوقعة للحصول على الرقمين اثنين وثلاثة. نعلم بالفعل أن الحصول على الرقم اثنين يتطلب 36 رمية في المتوسط. إذا حصلنا على الرقم ثلاثة أثناء انتظار الرقم اثنين، فلن نحتاج إلى رميات إضافية للحصول على الرقم ثلاثة. أما إذا لم يحدث ذلك، فسيتعين رمي النرد أكثر للحصول على الرقم ثلاثة.
احتمال ظهور الرقم ثلاثة هو 1/18، لذا يتطلب الأمر 18 رمية إضافية في المتوسط للحصول على الرقم ثلاثة، إذا ظهر الرقمان أولاً. بما أن هناك طريقة واحدة لظهور الرقمين، وطريقتين لظهور الرقم ثلاثة، فإن احتمال ظهور الرقمين أولاً هو 1/(1+2) = 1/3.
إذن، هناك احتمال بنسبة 1/3 أننا سنحتاج إلى 18 رمية إضافية للحصول على الرقم 3. وبالتالي، فإن عدد الرميات المتوقع للحصول على الرقمين 2 و3 هو 36 + (1/3) × 18 = 42.
بعد ذلك، فكّر في عدد الرميات الإضافية التي ستحتاجها للحصول على أربعة أيضًا. بحلول الوقت الذي تحصل فيه على الرقمين اثنين وثلاثة، إذا لم تحصل على أربعة بعد، فسيتعين عليك رمي النرد ١٢ مرة أخرى، في المتوسط، للحصول على واحد. هذا لأن احتمال الحصول على أربعة هو ١/١٢.
ما احتمال الحصول على أربعة قبل الحصول على اثنين وثلاثة؟ أولًا، لنراجع قاعدة شائعة للاحتمالات عندما لا يكون A وB متنافيين:
العلاقات العامة (أ أو ب) = العلاقات العامة (أ) + العلاقات العامة (ب) - العلاقات العامة (أ و ب)
تطرح pr(A وB) لأن هذا الاحتمال يُحسب مرتين في pr(A) + pr(B). إذًا،
pr(4 قبل 2 أو 3) = pr(4 قبل 2) + pr(4 قبل 3) - pr(4 قبل 2 و3) = (3/4)+(3/5)-(3/6) = 0.85.
احتمال عدم الحصول على الرقم أربعة في طريق الحصول على الرقمين اثنين وثلاثة هو 1.0 - 0.85 = 0.15. لذا، هناك احتمال بنسبة 15% للحاجة إلى 12 رمية إضافية. وبالتالي، فإن عدد الرميات المتوقع للحصول على الرقمين اثنين وثلاثة وأربعة هو 42 + 0.15 × 12 = 43.8.
بعد ذلك، فكّر في عدد الرميات الإضافية التي ستحتاجها للحصول على خمسة أيضًا. بحلول الوقت الذي تحصل فيه على الرقم من اثنين إلى أربعة، إذا لم تحصل على خمسة بعد، فسيتعين عليك رمي النرد 9 مرات أخرى، في المتوسط، للحصول على واحد، لأن احتمال الحصول على خمسة هو 4/36 = 1/9.
ما احتمال الحصول على الخمسة قبل تحقيق الاثنين، أو الثلاثة، أو الأربعة؟ القاعدة العامة هي:
pr (A أو B أو C) = pr(A) + pr(B) + pr(C) - pr(A و B) - pr(A و C) - pr(B و C) + pr(A و B و C)
إذن، pr(5 قبل 2 أو 3 أو 4) = pr(5 قبل 2)+pr(5 قبل 3)+pr(5 قبل 4)-pr(5 قبل 2 و3)-pr(5 قبل 2 و4)-pr(5 قبل 3 و4)+pr(5 قبل 2 و3 و4) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90. احتمال عدم الحصول على الرقم أربعة في الطريق إلى الرقمين اثنين وأربعة هو 1 - 83/90 = 7/90. لذا، هناك احتمال بنسبة 7.78% للحاجة إلى 7.2 رمية إضافية. وبالتالي، فإن العدد المتوقع للرميات للحصول على اثنين وثلاثة وأربعة وخمسة هو 43.8 + (7/90)*9 = 44.5.
استمر بنفس المنطق، لمجموع من ستة إلى اثني عشر. عدد العمليات الحسابية المطلوبة لإيجاد احتمال الحصول على الرقم التالي قبل الحاجة إليه هو عدد العمليات الحسابية، إذ يتضاعف الرقم الأخير تقريبًا في كل مرة. عند الوصول إلى اثني عشر، سيكون عليك إجراء 1023 عملية حسابية.
هذه هي القاعدة العامة لـ pr(A أو B أو C أو ... أو Z)
pr(A أو B أو C أو ... أو Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (A و B) - pr(A و C) - ... - pr(Y و Z) اطرح احتمال كل مجموعة من حدثين
+ pr (A و B و C) + pr(A و B و D) + ... + pr(X و Y و Z) أضف احتمال كل مجموعة من ثلاثة أحداث
- pr (A و B و C و D) - pr(A و B و C و E) - ... - pr(W و X و Y و Z) اطرح احتمال كل مجموعة من أربعة أحداث
ثم كرر العملية، وتذكر إضافة احتمالات الأحداث الفردية وطرح احتمالات الأحداث الزوجية. من الواضح أن هذا الأمر يصبح مملاً مع وجود عدد كبير من الأحداث المحتملة، مما يتطلب عملياً استخدام جدول بيانات أو برنامج حاسوبي.

يوضح الجدول التالي العدد المتوقع لكل خطوة. على سبيل المثال، ٣٦ للحصول على اثنين، و٤٢ للحصول على اثنين، وثلاثة. توضح الخلية اليمنى السفلية العدد المتوقع للرميات للحصول على جميع النتائج الإحدى عشرة، وهو ٦١٫٢١٧٣٨٥.

مشكلة العدد المتوقع لللفات

أعلى رقم مطلوب	احتمال	اللفات المتوقعة إذا لزم الأمر	الاحتمال غير مطلوب	الاحتمالية المطلوبة	إجمالي اللفات المتوقعة
2	0.027778	36.0	0.000000	1.000000	36.000000
3	0.055556	18.0	0.666667	0.333333	42.000000
4	0.083333	12.0	0.850000	0.150000	43.800000
5	0.111111	9.0	0.922222	0.077778	44.500000
6	0.138889	7.2	0.956044	0.043956	44.816484
7	0.166667	6.0	0.973646	0.026354	44.974607
8	0.138889	7.2	0.962994	0.037006	45.241049
9	0.111111	9.0	0.944827	0.055173	45.737607
10	0.083333	12.0	0.911570	0.088430	46.798765
11	0.055556	18.0	0.843824	0.156176	49.609939
12	0.027778	36.0	0.677571	0.322429	61.217385

تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .

Question 15

وفقًا لموقعCraps Advantage Players الإلكتروني، تستخدم كازينوهات لاس فيغاس بانتظام نردًا مرجحًا لزيادة نسبة السبعات، وبالتالي زيادة الأرباح. أنا مندهش! ماذا يقول الساحر عن هذا؟

Accepted Answer

يقول الساحر إن هذا الموقع يبدو وكأنه مجرد هذيان وثرثرة، دون أي دليل قاطع يبرر هذا الاتهام. سأكون سعيدًا بفضح أي كازينو يستخدم نردًا متحيزًا، لو كان لديّ أي دليل على ذلك.

إذا كان لدى أي شخص دليلٌ قاطع على وجود تحيز في النرد، فسأكون سعيدًا بفحصه ونشر استنتاجاتي. الأدلة التي أودّ رؤيتها هي إما ملفات سجلّات رميات النرد، أو الأفضل من ذلك، بعض النرد المُزعَم تحيزه.

وعلاوة على ذلك، إذا كانت الكازينوهات تستخدم بالفعل نردًا ينتج عددًا أكبر من المتوقع من السبعات، فلماذا لا يكون هؤلاء المحققون على علم بالمؤامرة التي تدور هناك والتي تراهن على عدم النجاح وتضع الاحتمالات؟

Question 16

جولة المكافأة "هوت رول" في ماكينات القمار تمنح اللاعب العدد التالي من العملات المعدنية بناءً على مجموع نردين. يستمر اللاعب في جمع العملات حتى يصل مجموعها إلى سبعة، وعندها تنتهي المكافأة. إذا حصل على سبعة في الرمية الأولى، يحصل على جائزة ترضية قدرها 70 عملة معدنية. فيما يلي جوائز جميع المجموعات الأخرى باستثناء السبعة:

2 أو 12: 1000
3 أو 11: 600
4 أو 10: 400
5 أو 9: 300
6 أو 8: 200

سؤالي هو ما هو متوسط الفوز بالمكافأة؟

2 أو 12: 1000
3 أو 11: 600
4 أو 10: 400
5 أو 9: 300
6 أو 8: 200

سؤالي هو ما هو متوسط الفوز بالمكافأة؟

Accepted Answer

انقر على الزر التالي للحصول على الإجابة.

الجواب هو 1983.33.

انقر على الزر التالي للحصول على الحل.

[حرق] ليكن x هو الجواب. ما دام اللاعب لم يحصل على سبعة، فيمكنه دائمًا توقع أن تكون انتصاراته المستقبلية x، بالإضافة إلى جميع انتصاراته السابقة. بمعنى آخر، هناك خاصية عدم التعلق بالذاكرة في رمي النرد، وهي أنه مهما رميت النرد، فلن تكون أقرب إلى سبعة مما كنت عليه في البداية.

لن أدخل في أساسيات احتمالات النرد، ولكن سأقول فقط أن احتمال كل مجموع هو كما يلي:

2: 1/36
3: 2/36
4: 3/36
5: 4/36
6: 5/36
7: 6/36
8: 5/36
9: 4/36
10: 3/36
11: 2/36
12: 1/36

قبل النظر في جائزة الترضية، يمكن التعبير عن قيمة x على النحو التالي:

x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)

بعد ذلك، اضرب كلا الطرفين في 36:

36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)

36x = 11200 + 30x

6x = 11200

x = 11,200/6 = 1866.67.

والآن قيمة جائزة الترضية هي 700*(6/36) = 116.67.

وبالتالي، فإن متوسط الفوز بالمكافأة هو 1866.67 + 116.67 = 1983.33.

[/spoiler]

يوصي المعالج

كرابس - النرد والتدحرج

نتائج مربع كاي

مشكلة العدد المتوقع لللفات

يوصي المعالج

كرابس - النرد والتدحرج

نتائج مربع كاي

مشكلة العدد المتوقع لللفات

شارك هذا