احتمال - بطاقات
كنت ألعب الباكارات عبر الإنترنت ومن أصل 75 يدًا فاز الموزع بـ 52 وفاز اللاعب بـ 23. وهذا فرق قدره 29، ما هو احتمال حدوث ذلك؟
أولاً، سأفترض أنك لا تحسب التعادلات. بمعنى آخر، تقصد 75 رهانًا تم حلها. من غير المرجح جدًا أن تمر 75 يدًا دون تعادل. العدد المتوقع لفوز المصرفي من أصل 75 رهانًا تم حلها هو 38.00913745. الانحراف المعياري هو الجذر التربيعي لحاصل ضرب 75، واحتمال فوز المصرفي، واحتمال فوز اللاعب. احتمال فوز المصرفي، بشرط عدم وجود تعادل، هو 0.506788499 واحتمال فوز اللاعب هو 0.493211501. وبالتالي، فإن الانحراف المعياري هو 4.329727904. بعد ذلك، سيتعين عليك إجراء تصحيح نصف نقطة للتوزيع الثنائي والبحث عن إحصائية Z في جدول طبيعي قياسي (هذه الخطوة متروكة للقارئ). الإجابة النهائية هي أن احتمال حصول المصرفي على 52 فوزًا أو أكثر هو 0.0009. سؤالك سمح أيضًا بإمكانية فوز المصرفي ٢٣ مرة أو أقل (بفارق ٢٩ مرة أو أكثر)، وهو احتمال قدره ٠٫٠٠٤. لذا، فإن الإجابة النهائية هي أن احتمال فارق ٢٩ مرة أو أكثر هو ٠٫٠٠١٣، أو ١ من ٧٦٩.
عندما أحسب مجموعات أوراق اللاعب والموزع في لعبة بوكر الكاريبي ستاد ، أحصل فقط على 3,986,646,103,440 مقابل مجموع أوراقك البالغ 19، وهكذا. أخطأتُ بمعامل 5 تمامًا. استخدمتُ مجموع الأوراق (52,5)*مجموع الأوراق (47,5). أين أخطأتُ؟ شكرًا، وأعتقد أن موقعك رائع.
شكراً على الثناء. أنت مخطئ بخمسة أضعاف لأن الموزع يستطيع الحصول على أي ورقة من أصل خمس ورقات مكشوفة. بمعنى آخر، الترتيب مهم في يد الموزع، لأن الورقة الأولى تُوزّع مكشوفة. الناتج الصحيح لمجموع المجموعات هو: combin(52,5)*47*combin(46,4) = 19,933,230,517,200.
ما هي احتمالات سحب ثلاث بطاقات لزوج والحصول على منزل كامل في لعبة البوكر ذات الخمس بطاقات؟
هناك طريقتان للحصول على فول هاوس في هذه الحالة: (١) سحب ثلاثة من نفس النوع، أو (٢) سحب بطاقة إضافية للزوج وزوج آخر. سأفترض أنك تتخلص من ثلاث بطاقات فردية.
أولاً، لنحسب عدد التركيبات تحت (1). هناك 3 رتب متبقية منها 3 مجموعات فقط (تذكر أنك تخلصت من 3 مجموعات فردية) و9 رتب متبقية منها 4 مجموعات. بالتالي، عدد التركيبات هو 3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39.
الآن، لنحسب عدد المجموعات تحت (2). يتبقى مجموعتان لإضافتهما إلى الزوج الحالي. هناك طريقتان لتكوين زوج من الصفوف الثلاثة مع بقاء 3 أوراق، وطريقة (4،2) لتكوين زوج من الصفوف مع بقاء 4 أوراق. لذا، فإن مجموع المجموعات تحت (2) هو 2*(3*مجموعة(3،2)+9*مجموعة(4،2)) = 2*(3*3 + 9*6) = 126. العدد الإجمالي لترتيب فل هاوس هو المجموع تحت (1) و(2)، أو 39+126=165. هناك طريقة (47،3)=16,215 لترتيب الصفوف الثلاثة في السحب الثاني. احتمال الحصول على فول هاوس هو عدد الطرق للحصول على فول هاوس مقسومًا على إجمالي التركيبات، أو 165/16215 = 0.0101758، أو حوالي 1 في 98.
لمزيد من المعلومات حول وظيفة combin()، يرجى الاطلاع على قسمي حول الاحتمالات في صفحة البوكر .
بدأتُ ألعب البوكر مع أصدقائي أسبوعيًا (خمس بطاقات سحب، ستاد، ستاد سبع بطاقات). لدينا سبعة لاعبين على الطاولة. يبدو لي أن احتمالية الفوز ستنخفض بشكل كبير نظرًا لتوزيع عدد اللاعبين على أوراق من مجموعة أوراق مكونة من 52 ورقة. هل لديكم صيغة رياضية تُرشدني إلى الطريق الصحيح؟
لا، احتمالية الحصول على أي يد متساوية بغض النظر عن عدد اللاعبين الآخرين على الطاولة. البطاقة غير المرئية تبقى غير مرئية، سواءً كان لدى لاعب آخر أو كانت لا تزال في المجموعة.
سمعتُ مؤخرًا قصةً لم أصدقها! أخبرني صديقٌ لي أنه في مباراة بوكر ودية في منزله، حصل هو وصديقه على ستريت فلش طبيعي في نفس اليد دون سحب أي أوراق! (في سحب خمس أوراق). أجد هذا الأمر صعب التصديق، ومن خلال موقعك، حسبتُ احتمالية الحصول على ستريت فلش واحد تقريبًا 65,000 إلى واحد، فما احتمالية الحصول على 2 في يد واحدة مع وجود 6 لاعبين في اللعبة (دون سحب أي أوراق؟).
سأقدم إجابة تقريبية بافتراض أن كل لاعب حصل على يد من مجموعة أوراق منفصلة. هذا لن يغير الاحتمالات كثيرًا. احتمالية حصول أي لاعب على ستريت فلاش، كما وردت في قسم الاحتمالات في البوكر، هي 36/2,598,960. لنُسمِّ هذا الاحتمال p. احتمالية حصول لاعبين على ستريت فلاش هي combin (6,2)* p2 *(1-p) 4 = 0.000000028779. بمعنى آخر، احتمالية عدم حدوث ذلك هي 347,477,740 إلى 1.
كيف يمكنك حساب الاحتمالات المنفصلة للحصول على: (1) الملكة عالية، (2) الملك عالية، و(3) الآس عالية في لعبة البوكر بثلاث بطاقات؟
سأحسب أولاً قيمة الملك، ثم أشرح بإيجاز صيغة المجموعتين الأخريين. الاحتمال هو عدد أوراق الملك مقسومًا على إجمالي عدد الأوراق. عدد الرتب الأقل من الملك هو 11. يجب أن تحتوي يد الملك على رتبتين مختلفتين. عدد طرق ترتيب مجموعتين من 11 هو الجمع (11، 2) = 55. ومع ذلك، فإن إحدى هذه المجموعات هي ملك-ملكة-ولد، مما ينتج عنه ستريت، لذا بطرح هذه المجموعة يتبقى 54 مجموعة لا تشكل ستريت. بعد ذلك، هناك أربع مجموعات لكل رتبة، أو 4 3 = 64 مجموعة ممكنة من المجموعات. ومع ذلك، فإن أربعًا من هذه المجموعات الـ 64 تنتج فلش، لذا يتبقى 64 - 4 = 60 مجموعة من المجموعات. لذا، فإن إجمالي عدد مجموعات الملك هو 54 × 60 = 3240. هناك مجموع (combin(52,3)=22,100) لترتيب 3 بطاقات من أصل 52. لذا، فإن احتمالية الحصول على أعلى عدد من أوراق الملك هي 3,240/22,100 = 0.1466063. واحتمالية الحصول على أعلى عدد من أوراق الآس هي: (combin(12,2)-2)*(4 3 -4)/combin(52,3)=0.1737557. لاحظ أن -2 بدلاً من -1 بسبب وجود مستقيمي a-2-3 وqka.
احتمال ارتفاع الملكة هو: (combin(10,2)-1)*(4 3 -4)/combin(52,3)=0.119457.
ما هي احتمالات الحصول على رويال فلاش؟ أو الحصول على رويال فلاش متسلسل (أمامي أم خلفي)؟
احتمال ظهور أيِّ فلش ملكي هو عدد أوراق الملكية المُحتملة، وهو أربعة (واحدة لكلِّ نوع)، مقسومًا على عدد طرق اختيار 5 أوراق من أصل 52، أي الجمع (52، 5) = 2,598,960. إذن، الإجابة هي 4/2,598,960 = 0.00000153908، أو 1 من 649,740.
احتمال ظهور فلاش ملكي متتالي يساوي (عدد الألوان) * (عدد الاتجاهات) / (إجمالي تبديلات 5 بطاقات من أصل 52) = 4 * 2 / التبديل (52، 5) = 8 / 311,875,200 = 8 / عدد البطاقات الملكية المحتملة، وهو أربعة (بطاقة واحدة لكل لون)، مضروبًا في عدد الاتجاهات التي يمكن أن تظهر فيها مقسومًا على عدد طرق اختيار 5 بطاقات من أصل 52، أي التبديل (52، 5) = 311,875,200. إذن، الإجابة هي 4/311,875,200 = 0.00000002565، أو 1 من 38,984,400.
أحب لعب بوكر الكاذبين بأوراق الدولار. ما احتمال ظهور أي رقم من نفس النوع على ورقة نقدية؟ شكرًا لك. إذا كنت ألعب مع ثلاثة أشخاص، فما احتمال ظهور أي رقم واحد؟
دعوني أولاً أجيب على السؤال غير المطروح حول احتمال ظهور رقم معين n مرة على ورقة نقدية عشوائية. تحتوي الورقة النقدية على 8 أرقام، لذا فإن احتمال ظهور رقم معين n هو: combin(8,n)*0.1 n *0.9 8-n /10 8. إليكم جدولًا يوضح احتمال ظهور رقم معين من 0 إلى 8.
احتمالات رقم محدد في لعبة البوكر الكاذبة
| رقم | احتمال |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| المجموع | 1.00000000 |
يوضح الجدول التالي احتمالية كل نوع ممكن من الأوراق النقدية، مُصنّفًا حسب عدد كل ن من نفس النوع. على سبيل المثال، الرقم التسلسلي 66847680 سيحتوي على ثلاثة أنواع، وزوج واحد، وثلاثة أنواع مفردة، باحتمالية 0.1693440.
الاحتمالات العامة في لعبة البوكر الكاذب
| 8 بلوط | 7 بلوط | 6 بلوط | 5 بلوط | 4 بلوط | 3 بلوط | 2 بلوط | 1 بلوط | احتمال |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| المجموع | 1.0000000 | |||||||
البلوط = "من نوع ما"
لمزيد من المعلومات، راجع صفحتي على liars poker .
مع مجموعة من 52 بطاقة، ما هي احتمالات سحب زوج من الولد؟
إذا افترضنا أنك تسحب خمس بطاقات، وتحسب كل الأيدي التي تحتوي على ورقتين فقط، فإن الاحتمال سيكون combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3.99%.
ما هو احتمال الحصول على ثلاثة أزواج في باي غاو بوكر؟ هل احتمال الحصول على ثلاثة أزواج متشابهة أقل أم أكبر؟
باستثناء ثلاثة من نوع واحد واثنين من الأزواج، فيما يلي طرق الحصول على ثلاثة أزواج وعدد من التركيبات.
لا توجد بطاقة عامة: combin(13,3)*10*6 3 *4 =2471040
البطاقة البرية المستخدمة للتنافس على زوج من الآسات: combin(12,2)*10*6 2 *4 2 = 380,160
البطاقة البرية المستخدمة كآس مفرد: combin(12,3)*6 3 = 47,520
العدد الإجمالي للمجموعات هو ٢٬٨٩٨٬٧٢٠. وهذا أقل من نصف عدد المجموعات البالغ ٧٤٧٬٠٦٧٦ لثلاثية متشابهة.
احتمالات الحصول على رويال فلش وفقًا لمعادلتك هي 4/2,598,960 = 1/649,740. لذا، إذا كنت ألعب لعبة "كاريبي ستاد" مع الموزع، فسيكون مجموع يدي ومجموع يدي الموزع 649,740 × 2 = 1,299,480. بناءً على ذلك، بعد 1,299,480 يدًا، يجب أن يكون هناك رويال فلش. أرجو إخباري إن كنت أفهم الاحتمالات بشكل صحيح.
أنت مُحق، ففي المتوسط، يحدث الفلاش الملكي مرة واحدة كل 649,740 يدًا، وأن العدد المتوقع للفلاش الملكي هو 2 في 1,299,480 يدًا. مع ذلك، هذا مجرد متوسط. مع كل يد تمر، لن تقترب من الحصول على الفلاش الملكي. تتميز كل لعبة تجارب مستقلة بهذه الخاصية، لذا فإن الفلاش الملكي لا يتأخر أبدًا.
احتمالية وجود صفر من الأوراق الملكية في 1,299,480 يدًا هي 13.53%.
مرحباً، أنا لاعب باي غاو بوكر دائم، ولاحظتُ أن موقعكم غني بالمعلومات المفيدة عن اللعبة. قبل أيام، عندما كنت ألعب مع صديقي، حصل على يد عالية برقم 9، وهي أقل يد ممكنة في رأيي. طوال فترة لعبي، لم أرَ هذا يحدث إلا مرة واحدة. ثم بعد خمس جولات، حصل على نفس اليد تماماً (2-3-4-5-7-8-9). لم نصدق ذلك، وكنا نتساءل عن احتمالات حدوث ذلك، ففكرنا في سؤالك. شكراً لوقتك وموقعك الرائع.
هناك طريقتان لترتيب الرتب لتشكيل يد عالية من 9، الطريقة التي ذكرتها، والطريقة 2-3-4-6-7-8-9. عدد مجموعات الألوان دون تكوين فلش هو 4 7 -4*(comb(7,5)*3^2+6*3+1) = 15,552. لذا، فإن احتمال الحصول على يد عالية من 9 هو 2*15,552/comb(53,7) = 31,104/154,143,080، أو 1 من 9,911. إذا لعبت خمس مرات فقط، فإن احتمال الحصول على يدين عاليتين من 9 سيكون 1 من 9,826,685. أعتقد أن حدوث ذلك هو مصادفة، وليس خللاً في مُولّد الأرقام العشوائية أو برمجة البرنامج.
سؤالي يتعلق بحسابات هامش الكازينو وعامل المخاطرة في لعبة "حرب الكازينو" وفقًا لقواعد كازينو نياجرا (أي، نسبة ربح 3-1 عند رفع الرهان وخسارة الرهان الأصلي). كيف توصلت إلى هذه الأرقام التي أحاول حسابها حاليًا؟ أواجه مشكلة. شكرًا لمساعدتك.
لنفترض أن d هو عدد مجموعات البطاقات. احتمال التعادل في الجولة الأولى هو (4*d-1)/(52*d-1) = 0.073955. احتمال التعادل في الجولة الثانية هو 12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0.073974. لنفترض أن p1 هو احتمال التعادل في الجولة الأولى، و p2 هو احتمال التعادل في الجولة الثانية. عندها، يكون عائد اللاعب هو p1 *(2* p2 +(1- p2 )/2*(1-2))= -0.023301. بضربه في -1، تكون نسبة ربح الكازينو 2.33%. آمل ألا أكون قد استعجلت في هذا.
هل يمكنك إخباري كيف تم التوصل إلى العدد الإجمالي للمجموعات في الكاريبي، وهو 19,933,230,517,200؟ لقد اتبعتُ مجموعاتك في لعبة البوكر ذات الخمس أوراق للحصول على 2,598,960. كيف أتابع من هنا؟ شكرًا لك مقدمًا.
لقد حسبتَ عدد مجموعات اللاعبين بشكل صحيح، حيث إن مجموع (52،5) = 2,598,960. ومن ثم، يمكن للموزع الحصول على مجموع (47،5) = 1,533,939 يدًا ممكنة. بعد ذلك، يمكن أن تكون أي بطاقة من بطاقات الموزع الخمس مكشوفة. إذن، 2,598,960 × 1,533,959 × 5 = 19,933,230,517,200.
أولاً، دعني أقول إن موقعك الإلكتروني رائع حقًا. لقد أخبرت بعض الأشخاص عنه، وآمل أن يجربوه أيضًا. أتمنى لك دوام النجاح. أعجبني أيضًا رابط WinPoker، وأعجبني WinPoker لدرجة أنني طلبته. إنه برنامج رائع. لدي سؤال أتمنى أن تساعدني فيه. أحاول معرفة عدد مرات ظهور كل يد في لعبة ستاد السبعة أوراق. لدي نسخة من جدولك للسبعة أوراق ، لكنني مهتم بالرياضيات للوصول إلى هذه الأرقام. أستطيع معرفة أرقام الخمسة أوراق، لكن الرقم السبعة يحيرني. أود إرسال ملف Excel 2000 بأرقامي. أود أيضًا معرفة كيفية حساب عدد المتتاليات في مجموعة من 53 ورقة باستخدام ورقة الجوكر. ساعدوني! ! !
شكراً لكلماتك الطيبة. أتفق معك أن حساب أرقام لعبة ستاد السبع بطاقات صعب. لهذا السبب أقوم بذلك على حاسوبي. يمر برنامجي بجميع التركيبات الممكنة ويسجل كل واحدة منها. عدد المتتاليات البرية في لعبة باي غاو بوكر هو 11 × (4 4 -4) + 10 × 3 × (4 4 -4) = 10332. بجمعها مع المتتاليات الطبيعية البالغ عددها 10200، يكون المجموع 20532.
أفهم احتمالات الحصول على رويال أو ستريت فلوش لأي شخص على طاولة بوكر الكاريبي ستاد أو ليت إت رايد، وكيف يتم حسابها. لكن سؤالي هو: كشخص يشاهد اللعبة من الخارج، ما هي احتمالات رؤية أي من هذه الأوراق تُوزّع على لاعب على الطاولة في أي توزيع معين؟ أعتقد أن الأمر يعتمد على عدد الأوراق في اللعبة... هل هي مجرد احتمالات الشخص مضروبة في عدد الأوراق في اللعبة؟ بمعنى آخر، رؤية رويال تُوزّع على أي يد مع أربعة لاعبين على الطاولة يعني 4x احتمالات الحصول على رويال؟ أنا محتار قليلاً!
طريقتك تقريب جيد. ومع ذلك، ووفقًا لهذا المنطق، عند رمي عملة معدنية، فإن احتمال ظهور وجه شخص واحد على الأقل من أصل 3 مرات يكون 3*50%=150%. وبافتراض أحداث مستقلة، فإن احتمال نجاح واحد على الأقل من أصل n محاولة، حيث يكون احتمال كل نجاح هو p، هو 1-(1-p) n . وفي حالة مثال رمي العملة المعدنية، سيكون هذا 1-.5 3 = 0.875. وفي حالة أربعة لاعبين في لعبة Caribbean Stud Poker، فإن احتمال ظهور فلاش ملكي واحد على الأقل سيكون 1-(1-4/2598960) 4 = 0.00000615629. ومع ذلك، نظرًا لأن جميع البطاقات يتم توزيعها من نفس المجموعة، فإن الأحداث ليست مستقلة. وتصبح الرياضيات معقدة للغاية لتحديد الإجابة الصحيحة الدقيقة، ويجب أن يكون التقريب قريبًا جدًا من الإجابة الصحيحة.
ما احتمال الحصول على سبع بطاقات متتالية في لعبة باي غاو بوكر؟ أعمل في كازينو، ورأيت هذا لأول مرة منذ خمسة عشر عامًا. ربح العميل المحظوظ 40,000 دولار.
هناك 32 احتمالًا لسلسلة متتالية طبيعية (4 صفوف × 8 نطاقات محتملة لـ 7 بطاقات). هناك 154143080 طريقة ممكنة لسحب 7 بطاقات من أصل 53. إذن، الإجابة هي 32/154143080، أو 1 من 4816971.
ما هو احتمال الحصول على مجموعتين متتاليتين متطابقتين من البطاقات (في كل من الرتب والنوع) في يدين متتاليتين في لعبة البوكر بثلاث بطاقات؟
احتمال الحصول على ستريت فلوش في اليد الأولى هو 4 × 12/مجموعة (52،3) = 48/22100 = ~ 0.0022. احتمال أن تكون اليد التالية متطابقة تمامًا هو 1/22100. لذا، الإجابة هي (48/22100) × (1/22100) = 48/488410000، بنسبة 1 من 10,175,208. هذا يزيد بنسبة 1.37 عن احتمال الفوز في يانصيب 6/49، والذي تبلغ احتماليته 1 من 13983816.
في لعبة الباكارات المكونة من 8 مجموعات من البطاقات، ما هو احتمال الحصول على الآس و8 من الماس لكل من اللاعب والمصرفي في نفس الصفقة؟
(8 2 /combin(416,2))* (7 2 /combin(414,2)) = 0.00000043، أو 1 في 2308093
شهدتُ مؤخرًا حدثًا غريبًا. كنتُ أشاهد لعبة بوكر بخمس بطاقات، حيث كان يُسمح بسحب بطاقتين فقط كحد أقصى. سحب لاعب بطاقة واحدة وأكمل فلاش القلب. سحب الموزع بطاقة واحدة، وأكمل فلاش البستوني. وبطبيعة الحال، كان فلاش الموزع أعلى. كان هناك ثلاثة لاعبين آخرين في اللعبة. ما احتمال وجود فلاشين في نفس اليد؟
لنحدد احتمالية الحصول على فلوش واحد عند التوزيع، أو سحب فلوش من 4 بطاقات. لتبسيط الأمر، سنفترض أن اللاعب سيسحب فلوشًا من زوج بات أو ستريت بـ 4 بطاقات. احتمالية الحصول على فلوش عند التوزيع (باستثناء ستريت/رويال فلاش) هي 4*(مجموع (13,5)-10)/مجموع (52,5) = 5108/2598960 = 0.0019654. احتمالية الحصول على فلوش من 4 بطاقات هي 4*3*مجموع (13,4)*13/مجموع (52,5) = 111540/2598960 = 0.0429172. احتمالية إكمال الفلش عند السحب هي 9/47. إذن، الاحتمال الإجمالي للحصول على فلوش من أربع بطاقات ثم إكماله هو 0.0429172*(9/47) = 0.0082182. وبالتالي، فإن الاحتمال الإجمالي للحصول على فلوش هو 0.0019654 + 0.0082182 = 0.0101836. واحتمال حصول لاعبين اثنين فقط من أصل خمسة على فلوش هو combin(5,2)* 0.0101836 2 *(1-00.0101836) 3 = 0.001006، أو حوالي 1 من 994.
أريد معرفة احتمالات حصول شخص ما على ٤ أوراق متشابهة خلال جولة من ٧ أوراق ستاد مع خمسة لاعبين ومجموعة أوراق واحدة. آمل أن تساعدوني، وشكرًا لوقتكم.
هناك طريقة لترتيب 7 بطاقات من أصل 52، وهي الجمع (combin(52,7)=133,784,560. عدد مجموعات البطاقات السبع، بما في ذلك مجموعة من أربع بطاقات متشابهة، هو 13*combin(48,3) = 224,848. يمثل العدد 13 عدد مراتب المجموعة، بينما يمثل الجمع (combin(48,3) عدد طرق اختيار 3 بطاقات من أصل 48 بطاقة متبقية. لذا، فإن الاحتمال هو 224,848/133,784,560 = 0.0017، أو 1 من 595.
عند فتح مجموعة أوراق جديدة، يكون ترتيبها من الآس إلى الملك من كل نوع. ما احتمالات إعادة ترتيب مجموعة أوراق مُخلطة إلى حالتها الأصلية من الآس إلى الملك؟
1 في 52 عامل، أو 1 في 80،658،175،170،943،900،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000،000.
إذا تم توزيع بطاقتين من مجموعة واحدة على عشرة أشخاص، فما احتمال أن يحصل لاعبان على زوج من الآسات؟
أولًا، هناك 10 × 9/2 = 45 طريقة لاختيار لاعبين من أصل 10. احتمال حصول لاعبين محددين على أربعة آسات هو 1/مجموعة (52، 4) = 1/270725. لذا، فإن احتمال حصول أي لاعبين على زوج من الآسات هو 45/270725 = 0.0001662.
إذا حصل سبعة لاعبين على سبع بطاقات، ما هو احتمال أن يحصل شخص واحد على الأقل على مجموعة مكونة من 7 بطاقات؟
احتمال حصول لاعب واحد على مجموعة مكونة من 7 بطاقات هو 4*combin(13,7)/combin(52,7) = 1 في 19491. احتمال حصول لاعب واحد على الأقل من أصل 7 لاعبين على مجموعة مكونة من 7 بطاقات هو حوالي 1 في 2785.
أعلم أن كل شيء ممكن رياضيًا، لكنني في الليلة الماضية في الكازينو، أعتقد أنني شهدتُ احتمالًا بنسبة مليار إلى واحد، وليس أن هذه الاحتمالات لا تحدث أبدًا. إليكم ما حدث: خلال 40 جولة (40 توزيعًا فرديًا بثلاث بطاقات، حوالي 8 جولات مع 5 لاعبين) على طاولة "ليت إت رايد"، تم توزيع 3 أوراق من نوع "أربعة متشابهة". بما أن احتمال توزيع أوراق من نوع "أربعة متشابهة" يبلغ حوالي 4100 إلى واحد، فما احتمال توزيع ثلاث أوراق من نوع "أربعة متشابهة" خلال 40 توزيعًا؟ أرجو الإجابة، فهذا يُرهقني. أنا من مُحبي هذه اللعبة منذ فترة طويلة.
لتبسيط الأمر، لنفترض أن كل يد مُوزّعة من مجموعة أوراق جديدة. احتمال ظهور أربعة من نفس النوع هو 13 × 48 / (combin(52,5) = 624 / 2598960. احتمال ظهور 3 من أصل 40 بطاقة من نفس النوع هو (combin(40,3) × p 3 * (1 - p) 37 = 1 من 7378135، حيث p = 624 / 2598960. لذا، فإن احتمالية ظهورها هي 1 من 7 ملايين.
أولاً، أردتُ أن أُخبرك بمدى إعجابي بموقعك الإلكتروني، وإعجابي بمهاراتك الرياضية. أستخدم ست مجموعات من أوراق البلاك جاك، وأضفتُ ثلاثة أوراق جوكر لأسبابٍ لن أضيع وقتك فيها، ولكن ما هي احتمالات توزيع أوراق الجوكر الثلاثة على لاعبٍ واحدٍ دفعةً واحدة؟ شكرًا جزيلًا لك.
أهلاً بك، شكراً على مجاملاتك. احتمال الحصول على ٣ أوراق جوكر متتالية من مجموعة أوراق بستة (بالإضافة إلى أوراق الجوكر الثلاثة) هو ١/مجموعة (٣١٥،٣) = ١ من ٥,١٥٩,٨٠٥. الحل الآخر هو (٣/٣١٥)*(٢/٣١٤)*(١/٣١٣).
ما احتمال توزيع ١٣ بطاقة على أربعة لاعبين باستخدام مجموعة أوراق من ٥٢ بطاقة، وكان جميع اللاعبين الأربعة يملكون سلسلة من الآس إلى اثنين؟ ليس بالضرورة أن تكون البطاقات من نفس النوع.
الإجابة هي (4 13 /COMBIN(52,13))* (3 13 /COMBIN(39,13))* (2 13 /COMBIN(26,13)) = 1 في 61,204,166,001.
ما هو احتمال أن يتم توزيع أربعة أوراق على ملكي؟
هناك أربع مجموعات محتملة للملكي. هناك خمس بطاقات مفقودة محتملة. يمكن أن تكون البطاقة الخامسة واحدة من 47 بطاقة أخرى. إذن، هناك 4 × 5 × 47 = 940 طريقة للحصول على أربع بطاقات ملكية. مجموع المجموعات (52، 5) = 2,598,960. لذا، الاحتمال هو 940/2,598,960 = 1 من 2,765.
عزيزي الساحر، لنفترض أننا خلطنا مجموعة أوراق لعب من 52 ورقة، وسحبنا 18 ورقة عشوائيًا، ووضعناها في 6 أكوام، كل منها يحتوي على 3 أوراق. ما احتمال أن تحتوي إحدى الأكوام على 3 أوراق آص (من أصل 4) بالضبط؟
الطريقة السهلة لحل المسألة هي أن احتمال وجود ثلاثة آسات في الكومة الأولى هو (4/52)*(3/51)*(2/50) = 1/5525. ومع ذلك، فإن احتمال وجود ثلاثة آسات في كل كومة متساوٍ، لذا نضرب في 6، فنحصل على 6/5525 = 0.001086.
ما هو احتمال الحصول على جميع البطاقات ذات الوجوه في لعبة الخمسة بطاقات؟
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0.00030474، أو حوالي 1 في 3282.
ما هو احتمال الحصول على اثنين من أربعة من نفس النوع خلال فترة ساعتين أثناء لعب لعبة Let it Ride؟
احتمال ظهور أربعة أوراق متشابهة في أي يد هو 13 × 48 / (combin(52,5) = 0.0002401. لنفترض أنه يمكنك لعب 120 يدًا خلال ساعتين. احتمال ظهور ورقتين متشابهتين تمامًا هو (combin(120,2) × 0.0002401 2 × (1-0.0002401) 118 = 0.000400095 = 1 في 2499.41.
في لعبة البوكر ذات الأربع بطاقات، ما هو الأرجح أن يكون ستريت أم فلش؟
باستثناء الفلاشات المتتالية والرويال فلاش، فإن احتمالية الحصول على ستريت هي ١.٠٢٪، واحتمالية الحصول على فلاش هي ١.٠٤٪. لذا، فإن احتمالية الحصول على فلاش أعلى بقليل.
ما احتمال استمرار جفاف "رويال فلاش" لمدة ٢٠٠ ألف يد على مدار مليون يد؟ أنا مهتم بالحل أكثر من الإجابة نفسها.
نادرًا ما أقول هذا، لكنني حاولتُ لساعات، لكنّ حساباتي في هذا الأمر كانت فوق طاقتي. لذا لجأتُ إلى صديقي وأستاذ الرياضيات غابور ميجيسي. إليكم صيغته لأيّ مسألة "جفاف".
- دع p يكون احتمال الفوز بأي يد معينة.
- ليكن d هو طول الجفاف.
- ليكن n هو عدد الأيدي التي تم لعبها.
- حدد k=dp و x=np.
- إذا كان k=1 فدع a=-1، وإلا فأوجد a بحيث يكون k=-ln(-a)/(1+a). (a هو رقم سلبي، إذا كان k>1 فإن -1 < a < 0، إذا كان k < 1 فإن a < -1، ويجب حساب a بدقة عالية.) [ملاحظة المعالج: يمكن العثور على هذا النوع من الحلول بسهولة في Excel باستخدام ميزة البحث عن الهدف ضمن قائمة الأدوات.]
- إذا كان k=1 فليكن A=2، وإلا فليكن A=(1+a)/(1+ak).
- احتمال عدم حدوث جفاف بطول d في n يد هو تقريبًا Ae a x .
في هذه المسألة تحديدًا، p=1/40391، d=200000، n=1000000، k=4.9516، x=24.758، a=-0.0073337، A=1.03007. لذا، فإن احتمال عدم حدوث جفاف هو 1.03007*e -0.0073337*24.758 = 0.859042. وبالتالي، فإن احتمال حدوث جفاف واحد على الأقل هو 1-0.859042 = 0.140958.
إليكم حل غابور ميجيسي الكامل المكون من خمس صفحات (PDF). شكرًا لك يا غابور على مساعدتك.
أجريتُ محاكاةً عشوائيةً لـ 32,095 مجموعةً من مليون يد. وكان العدد الذي شهد جفافًا واحدًا على الأقل هو 4558، باحتمالية 14.20%.
لنفترض أن لديك يدين بوكر من خمس أوراق موزعتين من مجموعتين منفصلتين. علمتَ أن اليد (أ) تحتوي على آس واحد على الأقل، واليد (ب) تحتوي على آس البستوني. أي يد يُحتمل أن تحتوي على آس إضافي واحد على الأقل؟
يوضح الجدول التالي احتمالية الحصول على من 0 إلى 4 آسات في يد عشوائية تمامًا.
احتمالات الآس - يد عشوائية
| الآسات | صيغة | التركيبات | احتمال |
|---|---|---|---|
| 0 | مجموعة(48,5) | 1712304 | 0.658842 |
| 1 | الجمع(4,1)×الجمع(48,4) | 778320 | 0.299474 |
| 2 | الجمع(4,2)×الجمع(48,3) | 103776 | 0.03993 |
| 3 | الجمع(4,3)×الجمع(48,2) | 4512 | 0.001736 |
| 4 | الجمع(4,4)×الجمع(48,1) | 48 | 0.000018 |
| المجموع | 2598960 | 1 |
إذا جمعنا بين ١ و٤ آسات، نجد أن احتمال ظهور آس واحد على الأقل هو ٠٫٣٤١١٥٨. واحتمال ظهور آسين أو أكثر هو ٠٫٠٤١٦٨٤.
يمكن إعادة صياغة احتمال وجود آص واحد على الأقل، بشرط وجود واحد على الأقل، وفقًا لنظرية بايز على النحو التالي: الاحتمال (آصان آخران مع وجود آص واحد على الأقل) = الاحتمال (آصان أو أكثر) / الاحتمال (آص واحد على الأقل) = 0.041684 / 0.341158 = 0.122185.
بالنسبة لأولئك الذين لا يعرفون نظرية بايز، فهي تنص على أن احتمال A مع إعطاء B يساوي احتمال A و B مقسومًا على احتمال B، أو Pr(A مع إعطاء B) = Pr(A و B)/Pr(B).
يوضح الجدول التالي التركيبات والاحتمالات لكل عدد من الآسات الأخرى بشرط إزالة الآس البستوني من المجموعة.
احتمالات الآس - اليد التي تم إزالة الآس منها
| الآسات | صيغة | التركيبات | احتمال |
|---|---|---|---|
| 0 | الجمع (3،0) × الجمع (48،4) | 194580 | 0.778631 |
| 1 | الجمع (3،1) × الجمع (48،3) | 51888 | 0.207635 |
| 2 | الجمع (3،2) × الجمع (48،2) | 3384 | 0.013541 |
| 3 | الجمع (3،3) × الجمع (48،1) | 48 | 0.000192 |
| المجموع | 249900 | 1 |
يُظهر هذا أن احتمالية الحصول على آص واحد على الأقل هي 0.221369.
للتسلية، دعونا نحل نفس السؤال باستخدام نظرية بايز. افترض أنه يتم توزيع أوراق عشوائية حتى يتم العثور على واحدة تحتوي على الآس البستوني. يمكن إعادة كتابة احتمال وجود آس إضافي واحد على الأقل، بشرط أن تحتوي اليد على الآس البستوني، على النحو التالي: الاحتمال (اثنين من الآس على الأقل بشرط وجود الآس البستوني في اليد). وفقًا لنظرية بايز، فإن هذا يساوي الاحتمال (اليد تحتوي على الآس البستوني وآس واحد على الأقل) / Pr (اليد تحتوي على الآس البستوني). يمكننا تقسيم البسط إلى الاحتمال (آسان بما في ذلك الآس البستوني) + الاحتمال (3 آسات بما في ذلك الآس البستوني) + الاحتمال (4 آسات). باستخدام الجدول الأول، يساوي هذا 0.039930 × (2/4) + 0.001736 × (3/4) + 0.000018 = 0.021285. احتمال ظهور الآس البستوني هو ٥/٥٢ = ٠٫٠٩٦١٥٤. لذا، فإن احتمال ظهور آسين على الأقل مع وجود الآس البستوني هو ٠٫٠٢١٢٨٥/٠٫٠٩٦١٥٤ = ٠٫٢٢١٣٦٩.
لذا فإن احتمال الحصول على اثنين أو أكثر من الآسات في حالة وجود آس واحد على الأقل هو 12.22%، وفي حالة وجود آس البستوني هو 22.14%.
حسناً، أُصدّق أرقامك، لكنها ما زالت غير منطقية بالنسبة لي. أعتقد أن الاحتمالات متساوية. ما الفرق بين نوع الورقة والآس الذي لديك؟
لنلقِ نظرة على حالة أبسط. لنفترض أن المرأة (أ) قالت: "لديّ طفلان، أحدهما على الأقل ولد". قالت المرأة (ب): "لديّ طفلان، والأكبر اسمه جون". يمكننا افتراض أنه لا يوجد أي طفل اسمه جون بنت، ولا تُطلق أي امرأة نفس الاسم على أكثر من طفل واحد. باستخدام الاحتمال الشرطي، يكون احتمال أن يكون كلا الطفلين ولدًا للمرأة (أ) هو pr(كلاهما ولدان)/pr(واحد على الأقل ولد) = pr(كلاهما ولدان)/(1-pr(كلاهما بنتان)) = (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3. مع ذلك، فإن احتمال أن يكون الطفل الأصغر للمرأة (ب) ولدًا، أو أن يكون كلا الطفلين ولدين، هو ؟، لأن القول بأن اسم الطفل الأكبر جون لا يُخبرنا شيئًا عن الطفل الأصغر.
لنفترض أنك ذهبت إلى جيفّي لوب، وقدّموا عرضين بنفس السعر. العرض (أ) يفحصون أربعة قطع ويستبدلون أول قطعة معيبة فقط. أما العرض (ب) فيفحصون مشكلة واحدة فقط ويصلحونها إن وُجدت. ألا تفضل اختيار العرض (أ)؟ وصلت سيارتك بنفس عدد القطع التالفة المتوقعة، لكن احتمالية وجود مشكلة أكبر في العرض (أ)، وبالتالي ستغادر مع عدد أقل من القطع المعيبة المتوقعة بموجب هذه الخطة. وبالمثل، فإن اختبار أي ورقة آص من المرجح أن يُظهر الورقة الآص الوحيدة، بينما اختبار ورقة آص البستوني لا يفحص الأوراق الثلاثة الأخرى، مما يزيد من احتمالية كونها أوراق آص.
كيف وصلت إلى 2072 لعدد الفلاشات المستقيمة باستخدام 4 بطاقات من أصل 5 في لعبة البوكر ذات الأربع بطاقات؟
أولاً، قمت بتقسيم الفلاشات المتتالية إلى نوعين، تلك التي تحتوي على أربع بطاقات متتالية من نفس النوع وتلك التي تحتوي على خمس بطاقات. عدد الفلاشات المتتالية المكونة من خمس بطاقات هو عدد الأنواع * عدد السلاسل (من الآس إلى 10 كأقل بطاقة) = 4 * 10 = 40. يوجد في الفلاشات المتتالية المكونة من أربع بطاقات 11 سلسلة مختلفة (من الآس إلى الولد كأقل بطاقة). في حالة الفلاشات المتتالية A234 و JQKA، يمكن أن تكون البطاقة الخامسة واحدة من 47 (52 ناقصًا البطاقات الأربع التي تمت إزالتها بالفعل والبطاقة الخامسة التي ستشكل فلاشًا متتاليًا مكونًا من 5 بطاقات، والتي تم احتسابها بالفعل). لذا يوجد 4 * 2 * 47 = 376 فلاشًا متتاليًا من الامتداد A234 أو JQKA. من بين التسع الأخرى، يوجد 46 بطاقة محتملة للبطاقة الخامسة (52 ناقصًا البطاقات الأربع التي تمت إزالتها بالفعل واثنتان للبطاقات التي ستشكل فلاشًا متتاليًا مكونًا من خمس بطاقات). لذا فإن عدد الفلاشات المتتالية من الامتداد 2345 إلى TJQK هو 4 * 9 * 46 = 1656. وبالتالي فإن العدد الإجمالي للمجموعات المتتالية المكونة من 4 بطاقات هو 40 + 376 + 1656 = 2072.
من الممكن الحصول على فلاش بنسبة ١٠٠٪ على البطاقة السابعة عشرة الموزعة مهما كانت الظروف. متى يكون الحصول على ستريت بنسبة ١٠٠٪ على أي بطاقة موزعة؟
يُضمن الحصول على ستريت فقط بـ 45 بطاقة. على سبيل المثال، يمكنك توزيع كل من A، 2، 3، 4، 6، 7، 8، 9، JQ، وK بإجمالي 44 بطاقة، ومع ذلك لن تحصل على ستريت.
عزيزي السيد ساحر الاحتمالات الرائع، أنا منبهر تمامًا بذكائك الإحصائي. هل يمكنك بالصدفة حساب احتمال ظهور سبع بطاقات متتالية - أي A، 2، 3، 4، 5، 6، 7 أو 2، 3، 4، 5، 6، 7، 8 أو 7، 8، 9، 10، ولد، ملكة، ملك في لعبة ستاد السبع بطاقات؟ نحن ندرك أن هذه ليست يد بوكر حقيقية؛ ومع ذلك، ظهرت أثناء اللعب وكنا نتساءل إن كان احتمالها أقل من احتمالية ظهور فل هاوس عادي في لعبة ستاد السبع بطاقات. مع خالص التحيات، أيها الخبير.
كيف لي أن أرفض بعد أن أطريتني بهذه الطريقة؟ أولًا، هناك مجموع (52، 7) = 133,784,560 طريقة لاختيار 7 بطاقات من أصل 52، بغض النظر عن الترتيب. هناك 8 نطاقات ممكنة لسلسلة من 7 بطاقات (أقل بطاقة يمكن أن تكون من A إلى 8). إذا كان لدينا 7 رتب مختلفة، فهناك 4 7 = 16384 طريقة لترتيب الأنواع. لاحظ أن هذا يشمل جميع الأنواع نفسها، والتي ستشكل سلسلة متتالية. لذا، فإن الاحتمال هو 8 × 16,384 / 133,784,560 = 1 في 1020.6952.
من مجموعة واحدة من البطاقات، إذا قمت بتوزيع 4 بطاقات، ما هي احتمالات أن تكون بطاقة واحدة على الأقل من نوع البستوني؟
احتمال عدم وجود أي بستوني هو (39/52)*(38/51)*(37/50)*(36/49) = 0.303818. لذا، فإن احتمال وجود بستوني واحد على الأقل هو 1-0.303818 = 0.696182.
في لعبة ذات مجموعة أوراق واحدة، ما احتمال الحصول على آس واثنين على الأقل من أربع أوراق؟ من المفيد معرفة ذلك في لعبة أوماها.
من الاحتمالية ١٠١، نعلم أن احتمالية (أ أو ب) = احتمالية (أ) + احتمالية (ب) - احتمالية (أ و ب). إذًا، احتمالية (أ و ب) = احتمالية (أ) + احتمالية (ب) - احتمالية (أ أو ب). لنفترض أن (أ) يحصل على آص، و(ب) يحصل على اثنين. احتمالية (أ) = احتمالية (آص واحد على الأقل) = احتمالية (بدون آص) = احتمالية (48،4) / احتمالية (52،4) = 1-0.7187 = 0.2813. من البديهي أن احتمالية عدم الحصول على اثنين متساوية. بنفس المنطق، احتمال الحصول على آس أو اثنين على الأقل = احتمال الحصول على آس واحد أو اثنين = احتمال الحصول على واحد (بدون آسات ولا اثنين) = احتمال الحصول على واحد (44،4) / احتمال الحصول على واحد (52،4) = 1 - 0.501435 = 0.498565. لذا، احتمال الحصول على آس واحد واثنين على الأقل هو 0.2813 + 0.2813 - 0.498565 = 0.063962.
ما هي احتمالات الحصول على جاك الماس 27 مرة متتالية في لعبة مكونة من ستة بطاقات؟
احتمال الفوز بأي يد هو ٦/٥٢. احتمال الفوز ٢٧ يدًا متتالية هو (٦/٥٢) ٢٧ = ١ من ٢٠,٩٨٩,٧١٣,٨٤٢,١٦١,٨٠٠,٠٠٠,٠٠٠.
ما هو احتمال الحصول على "يد الرجل الميت"، وهي زوجان من الآسات والثمانيات؟
هناك ست طرق لترتيب مجموعتين من أصل أربع لكل زوج. ثم هناك 44 بطاقة للبطاقة المفردة. لذا، فإن عدد التركيبات الناجحة هو 6 × 6 × 44 = 1584. يبلغ إجمالي التركيبات 2,598,960، لذا فإن الاحتمال هو 0.0609%.
أفهم أنك أجبت بالفعل على احتمال الحصول على "يد الرجل الميت"، وهي زوجين من الآسات والثمانيات، وهو 0.0609٪ في 3 أبريل 2005 ، ولكنني أعتقد أن يد الرجل الميت هي "اثنين من الآسات السوداء واثنين من الثمانيات السوداء وملكة الأندية" ما هو احتمال سحب تلك اليد بالضبط من مجموعة قياسية واحدة؟
هناك طريقة واحدة فقط للحصول على تلك اليد بالضبط. لذا، الاحتمال هو ١ في المجموعة (٥٢،٥) أو ١ في ٢,٥٩٨,٩٦٠.
ما هي احتمالات كل يد من خمس بطاقات يُمكن توزيعها من مجموعة أوراق قياسية من 52 بطاقة، حيث يُعتبر نوع بطاقة واحدة غير مكررة في اليد عامًا؟ على سبيل المثال، لنفترض أن اليد A♠ A♣ A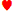 أ
أ ٢. في هذه اليد، يُهمَل لون الرقم ٢، ويُمثّل أيًا من الأوراق الأربعة التي تحمل الرقم ٢ في المجموعة. مثال آخر هو AJ-٨-٦-٥. في هذه اليد، يُهمَل لون جميع الأوراق الخمس، بحيث لا يمكن الحصول إلا على تركيبة واحدة من هذا النوع. مثال آخر: ٣♠ ٣
٢. في هذه اليد، يُهمَل لون الرقم ٢، ويُمثّل أيًا من الأوراق الأربعة التي تحمل الرقم ٢ في المجموعة. مثال آخر هو AJ-٨-٦-٥. في هذه اليد، يُهمَل لون جميع الأوراق الخمس، بحيث لا يمكن الحصول إلا على تركيبة واحدة من هذا النوع. مثال آخر: ٣♠ ٣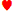 ٧♣ ٧♠ Q. في هذه اليد، لا يُستهان بنوع ورقتي ٣ و٤ لوجود أكثر من ورقة واحدة في اليد، ولكن نوع ورقة Q عام. بمعنى آخر، يُستهان بنوع أي ورقة غير مكررة في اليد، وتُعتبر تلك اليد إحدى الأيدي المحتملة، مع وجود احتمالات عديدة لتكرار اليد إذا لم تُستهان بنوع كل ورقة. وهكذا، تتكون سلسلة متتالية أو متتالية من خمس أوراق محددة؛ مثلاً Q.
٧♣ ٧♠ Q. في هذه اليد، لا يُستهان بنوع ورقتي ٣ و٤ لوجود أكثر من ورقة واحدة في اليد، ولكن نوع ورقة Q عام. بمعنى آخر، يُستهان بنوع أي ورقة غير مكررة في اليد، وتُعتبر تلك اليد إحدى الأيدي المحتملة، مع وجود احتمالات عديدة لتكرار اليد إذا لم تُستهان بنوع كل ورقة. وهكذا، تتكون سلسلة متتالية أو متتالية من خمس أوراق محددة؛ مثلاً Q.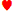 ج♣ 10
ج♣ 10 9
9 8♠ أو A♠ J♠ 8♠ 7♠ 3♠ لا يمكن أن تظهر إلا مرة واحدة، لأن أي تركيبة أخرى من نفس البطاقات، حتى لو كانت من نوع مختلف، ستكون تكرارًا. لذا، باستخدام هذا المعيار، ما هو مجموع نقاط أي يد واحدة يتم توزيعها؟ بمعنى آخر، كم عدد هذه الأيدي المكونة من خمس بطاقات في مجموعة أوراق قياسية من 52 بطاقة؟ شكرًا لمشاركتك.
8♠ أو A♠ J♠ 8♠ 7♠ 3♠ لا يمكن أن تظهر إلا مرة واحدة، لأن أي تركيبة أخرى من نفس البطاقات، حتى لو كانت من نوع مختلف، ستكون تكرارًا. لذا، باستخدام هذا المعيار، ما هو مجموع نقاط أي يد واحدة يتم توزيعها؟ بمعنى آخر، كم عدد هذه الأيدي المكونة من خمس بطاقات في مجموعة أوراق قياسية من 52 بطاقة؟ شكرًا لمشاركتك.
أنا مُلِمٌّ بهذا المفهوم جيدًا. هناك 134,459 يدًا فريدة من خمس أوراق. والسبب الذي يجعلني أعرف أن هذا أول برنامج فيديو بوكر لي، حلل جميع الأيدي المحتملة البالغ عددها 2,598,960 يدًا، واستغرق أيامًا لتحليل جدول الأرباح. ومع ذلك، من خلال تشغيل يد واحدة فقط من كل فئة من فئات الأيدي البالغ عددها 134,459 يدًا، مع مراعاة عدد الأيدي في فئتها، يُمكنك تقليل وقت التشغيل بنسبة 95%. أحيانًا، عندما تكون اللعبة مُحددة بنوع معين، كما في تحليلي الأخير للعبة بلاك جاك بونس بوكر ، أضطر إلى إعادة تشغيل برنامجي القديم واللعب ببطء.
ما هي الاحتمالات في لعبة Five Card Stud باستخدام مجموعة من 5 بدلا من 4؟
التركيبات في لعبة البوكر ذات الخمس بدلات
| يُسلِّم | التركيبات | احتمال | صيغة |
| خمسة من نفس النوع | 13 | 0.000002 | 13 |
| فلاش مستقيم | 50 | 0.000006 | 5*10 |
| أربعة من نفس النوع | 3900 | 0.000472 | 13*12* مجموعة (5,4)*5 |
| تدفق | 6385 | 0.000773 | 5*(الجمع(13,5)-10) |
| منزل كامل | 15600 | 0.001889 | 13*12*الجمع(5,3)*الجمع(5,2) |
| مستقيم | 31200 | 0.003777 | 10*(5^5-5) |
| ثلاثة من نفس النوع | 214500 | 0.025969 | 13*كومبين(12,2)*كومبين(5,3)*5^2 |
| زوجان | 429000 | 0.051938 | كومبين(13,2)*11*كومبين(5,2)^2*5 |
| زوج | 3575000 | 0.432815 | 13*كومبين(12,3)*كومبين(5,3)*5^3 |
| لا شئ | 3984240 | 0.48236 | (الجمع (13،5) - 10) * (5 ^ 5 - 5) |
| المجموع | 8259888 | 1 |
لاحظ أنني قمت بعكس ترتيب البيت الكامل والفلاش.
كم عدد مجموعات البطاقات الخمس في مجموعة أوراق اللعب القياسية التي تحتوي على بطاقات من مجموعتين فقط؟
يمكن تقسيم البدلتين إما إلى 4 و1 أو 3 و2. لنلقِ نظرة على نسبة 4/1 أولًا. هناك 4 بدل للاختيار من بينها للبدلة ذات 4 أوراق، و3 بدل متبقية للبدلة ذات ورقة واحدة. هناك 715 طريقة لاختيار 4 رتب من أصل 13. وهناك 13 طريقة لاختيار رتبة واحدة. إذن، هناك 4×3×715×13=111,540 طريقة لتقسيم 4/1 بين البدلتين. وبنفس المنطق، هناك 4×3×البدل(13,3)×البدل(13,2)=267,696 طريقة لتقسيم 3/2. لذا، الاحتمال الكلي هو (111,540+267696)/البدل(52,5) = 14.59%.
ما هي احتمالات الحصول على بطاقة ٢-٣-٤-٥-٧ غير متطابقة؟ شكرًا جزيلاً، الموقع رائع!
شكرا. (4 5 -4)/combin(52,5) = 1020/2598960 = 1 في 2,548.
كنتُ في فوكسوودز قبل أيام، أشاهد آخر طاولتين من بطولة فوكسوودز بوكر كلاسيك. عندما دخل فينس فان باتن (أحد مُضيفي جولة البوكر العالمية) للمشاهدة، بدأ يُجري جميع أنواع الرهانات الدعائية مع بعض مُحترفي البوكر المُتواجدين. كان يُقدم لأي شخص رهانًا بنسبة ٢٠ إلى ١ إذا استطاع قلب مجموعة أوراق كاملة، مُتنقلًا بين الصفوف، قائلين بصوت عالٍ أثناء سحب كل ورقة: الآس، ٢، ٣، ٤، وهكذا حتى الملك، والبدء من جديد من الآس دون ظهور الورقة التي يُعلن عنها. لم يُكمل أحدٌ اللعب، وربح فينس بضع مئات من الدولارات في حوالي ١٠ دقائق قبل أن يستسلم الجميع. أعلم أن هذا مُمكن، لكن لديّ شك في أن فينس يُقدم رهانًا مُبالغًا فيه بنسبة ٢٠ إلى ١ فقط. ما هي احتمالات إنهاء المجموعة بأكملها؟
طريقة بسيطة لتقدير احتمال الفوز هي افتراض أن كل بطاقة لديها احتمال ١٢/١٣ لعدم مطابقة الترتيب المذكور. للفوز بهذا الرهان، على الضحية تكرار ذلك بنجاح ٥٢ مرة. احتمال الفوز ٥٢ مرة هو (١٢/١٣) ٥٢ = ١.٥٦٪. السعر العادل هو ٦٣.٢ إلى ١. عند ٢٠ إلى ١، كانت أفضلية فينس ٦٧.٣٪ (يا للعجب!).
وفقًا لـ GM، وهو عالم رياضيات أفضل مني، فإن الاحتمال الفعلي هو 1.6232727%. سبب الاختلاف هو أن نتيجة كل اختيار مرتبطة ارتباطًا إيجابيًا بالاختيارات السابقة.
أثناء اللعب الليلة الماضية، كان أحد اللاعبين، وهو لاعب عجوز ماكر أشعث عدواني، يتحدى الطاولة لتحقيق رهانات جانبية متساوية على الطاولة. كان هذا اللاعب العجوز المتذمر يراهن على أن إحدى البطاقات الثلاث على الطاولة ستكون إما آس أو 2 أو ولد (وأحيانًا كان يغير البطاقات الثلاثة المميزة). ما هي احتمالات هذا الرهان؟ سنكون شاكرين جدًا لحكمتك الحكيمة.
قبل ظهور أي بطاقات، احتمال عدم ظهور أي ثلاث رتب على الطاولة هو: كومبين (40،3) / كومبين (52،3) = 9880 / 22100 = 44.71%. لذا، كانت نسبة تفوق هذا اللاعب 10.59%.
لنفترض أن خمس أوراق من مجموعة أوراق مكونة من 52 ورقة، وأول ورقة منها ملك. ما احتمال وجود ملك إضافي واحد على الأقل؟ رأيتُ مسألة آص كنتَ تحلها، لكنني لم أستطع فهمها. شكرًا لك على أي مساعدة.
الطريقة التي أُفضّلها للإجابة على أسئلة الاحتمالات هي استخدام الدالة التوافقية. بهذه الطريقة، هناك 194,580 طريقة لاختيار أربع أوراق ليست ملكًا من بين 48 ورقة ليست ملكًا في المجموعة. وهناك 249,900 طريقة لاختيار أي أربع أوراق من بين 51 ورقة متبقية في المجموعة. لذا، فإن احتمال عدم وجود أي أوراق ملك في الأوراق الأربع التالية هو 194,580/249,900 = 77.86%. وبالتالي، فإن احتمال الحصول على نوع واحد على الأقل هو 100% - 77.86% = 22.14%.
قال العديد من الأشخاص إن الدالة التوافقية ربما تكون فوق مستوى فهم من يطرحون أسئلة الاحتمالات البسيطة هذه. لا أختلف معهم في ذلك، ولكن أحد أهم أسباب إنشاء هذا الموقع هو محاولة تعليم قرائي شيئًا عن الرياضيات. الدالة التوافقية مفيدة للغاية في الاحتمالات، وتوفر الكثير من الوقت. ومع ذلك، يمكن بسهولة الإجابة على السؤال المطروح بدونها.
احتمال ألا تكون الورقة الثانية ملكًا هو 48/51. ذلك لوجود 48 ورقة غير ملك متبقية في المجموعة، أي 51 ورقة إجمالية متبقية. إذا لم تكن الورقة الثانية ملكًا، فإن احتمال ألا تكون الورقة الثالثة ملكًا أيضًا هو 47/50 (47 ورقة غير ملك مقسومة على 50 ورقة متبقية). باتباع هذا حتى النهاية، يكون احتمال ألا تكون أيٌّ من الأوراق الأربع الأخرى ملكًا هو (48/51) × (47/50) × (46/49) × (45/48) = 77.86%. واحتمال عدم وجود ملك واحد على الأقل هو 100% - 77.86% = 22.14%.
أولاً، اختر 5 بطاقات من مجموعة أوراق لعب واحدة مكونة من 52 بطاقة. ثانياً، اجمع قيمها في البلاك جاك (T، J، Q، K = 10، A = 1). ما احتمال أن يكون المجموع زوجياً/فردياً؟ أعتقد أنه مع كثرة البطاقات الزوجية، يزداد احتمال أن يكون المجموع زوجياً.
المفاجأة، احتمالية الحصول على مجموع فردي هي ٥٠.٠٣٪، مع أن ٣٠ من أصل ٥٢ بطاقة زوجية. يوضح الجدول التالي احتمالية كل تقسيم زوجي/فردي.
سؤال فردي/زوجي
| حتى | احتمال | التركيبات | احتمال | مجموع |
| 0 | 5 | 15504 | 0.005965 | غريب |
| 1 | 4 | 155040 | 0.059655 | حتى |
| 2 | 3 | 565440 | 0.217564 | غريب |
| 3 | 2 | 942400 | 0.362607 | حتى |
| 4 | 1 | 719200 | 0.276726 | غريب |
| 5 | 0 | 201376 | 0.077483 | حتى |
| المجموع | 2598960 | 1 |
ما هي احتمالات إذا قمت بسحب ثلاث بطاقات من مجموعة البطاقات أن تكون واحدة منها فقط هي البستوني؟
احتمال أن تكون الورقة الأولى بستوني، والبطاقتان الثانيتان ليستا كذلك، هو (13/52)×(39/51)×(38/50) = 14.53%. ثم اضرب هذا العدد في 3، لأن البستوني قد يكون أيًا من الأوراق الثلاث. إذن، الإجابة هي 3×14.53% = 43.59%. ولمن يفضل الدالة التوافقية، الإجابة هي 13×combin(39,2)/ combin (52,3) = 9,633/22,100 = 43.59%.
اختر رقمين عشوائيين بين ٠ و١ (موزعين بالتساوي). الآن، اختر الأصغر. ما هو متوسط هذا الاختيار؟ ماذا عن الحالة العامة لعدد n من الأرقام؟
لعددين، الإجابة هي ١/٣، ولعدد n عدد هي ١/(ن+١). نشرتُ حلولَ مسائل الرياضيات ، السؤالان ١٩٤ و١٩٥.
أنت تلعب لعبةً تضم ثلاثة أشخاص: (أ) أنت، (ب) خصمك، و(ج) حكم. يختار كلٌّ منكم رقمًا حقيقيًا بين 0 و1 سرًا. بمجرد اختيار جميع الأرقام، تُكشف. اللاعب الذي خمن أقرب رقم إلى رقم الحكم، دون تجاوزه، يفوز. إذا كنت أقرب، تربح دولارًا واحدًا. إذا كان خصمك أقرب، تخسر دولارًا واحدًا. إذا تجاوز كلا اللاعبين الرقم، أو تعادلا، تُعتبر اللعبة متعادلة.
هل هناك رقم يمكنك اختياره ليُحقق أقصى عائد مُتوقع، إذا اختار اللاعب الآخر عشوائيًا؟ ماذا لو كان لدى اللاعب الآخر استراتيجية أيضًا؟
أتمنى أن تكون سعيدًا، فقد قضيتُ اليوم كله في الجزء الثاني، وما زالت إجابتي خاطئة. لئلا أحرم قرائي من نفس المتعة، لن أكشف الإجابات هنا. لقد قسمتُ المسألة إلى مسألتين، ونشرتُ الإجابات والحلول على موقع mathproblems.info ، المسألتان ١٩٦ و١٩٧.
إذا قمت باختيار خمس بطاقات عشوائيًا من مجموعة بطاقات قياسية مكونة من 52 بطاقة، ما هو احتمال أن تكون جميع البطاقات الأربع ممثلة؟
يجب أن يكون هناك نوع واحد من البطاقات ببطاقتين، وثلاث بطاقات ببطاقة واحدة لكل بطاقة. هناك أربع أنواع محتملة للنوع الذي يُمثل مرتين. بالنسبة للنوع الذي يُمثل مرتين، هناك 78 طريقة لاختيار رتبتين من أصل 13. لكل نوع من الأنواع الثلاثة الأخرى، هناك 13 رتبة محتملة لكل نوع. إذن، العدد الإجمالي للتركيبات هو 4 × 78 × 13 × 13 × 13 = 685,464. هناك 2,598,960 طريقة لاختيار 5 بطاقات من أصل 52. إذن، الاحتمال هو 685,464 / 2,598,960 = 26.37%.
ما احتمال ظهور أي رتبتين مختارتين، مثل الملكة والملك، بشكل متتالي في مجموعة عشوائية؟ تحداني أحدهم بمراهنة متساوية على حدوث ذلك.
وفقًا لمحاكاة عشوائية، الاحتمال هو ٤٨٫٦٤٪. لذا، كنت سأراهن.
هل يمكنك أن توصي بوظيفة لربط أي خمس بطاقات من مجموعة مكونة من 52 بطاقة إلى عدد صحيح من 0 إلى 2,598,959؟
نعم. أولًا، عيّن لكل بطاقة قيمة من ٠ إلى ٥١. رتّب البطاقات من c1 إلى c5، بحيث تكون c1 الأقل قيمةً وc5 الأعلى قيمةً. ثمّ استدعِ الدالة التالية:
int GetIndex(int c1, int c2, int c3, int c4, int c5)
{
إرجاع combin(c5,5) + combin(c4,4)+ combin(c3,3) + combin(c2,2) + combin(c1,1);
}
حيث تقوم الدالة combin بإرجاع القيمة التقليدية، إلا إذا كانت القيمة الأولى أقل من القيمة الثانية، فتقوم بإرجاع 0، كما يلي:
int combin(int x, int y)
{
إذا (y>x)
العودة 0؛
آخر
{
int i,n؛
ن=1؛
بالنسبة إلى (i=x-y+1؛ i<=x؛ i++)
ن*=ي؛
لـ (i=2؛ i<=y؛ i++)
ن/=أنا؛
العودة ن؛
}
}
إذا كنت تفعل هذا للوصول إلى عنصر المصفوفة، فقم بتحميل المصفوفة على النحو التالي.
العد=0؛
لـ (c5 = 4؛ c5 < 52؛ c5++)
{
لـ (c4 = 3؛ c4 < c5؛ c4++)
{
لـ (c3 = 2؛ c3 < c4؛ c3++)
{
لـ (c2 = 1؛ c2 < c3؛ c2++)
{
لـ (c1 = 0؛ c1 < c2؛ c1++)
{
index_array[count]=مهما كنت ترغب؛
العد++؛
}
}
}
}
}
ما هو احتمال سحب 3 من أصل 10 فلاشات متتالية، مع الاحتفاظ بثلاثة في فلاشة متتالية مع وجود فجوة واحدة؟

هذه مسألة توزيع ثنائي. الصيغة العامة هي أنه إذا كان احتمال وقوع حدث ما هو p، وكانت كل نتيجة مستقلة، فإن احتمال وقوعه بالضبط w من t تجارب هو combin (t,w)×p w ×(1-p) tw .
في هذه الحالة، هناك طريقتان للحصول على ستريت فلش. ستحتاج إلى 8 من الماس وورقة أخرى من 6 أو J من الماس. هناك combin(47,2)=1,081 طريقة لسحب ورقتين من أصل 47 ورقة متبقية في المجموعة. لذا، فإن احتمال الحصول على ستريت فلش في أي يد هو 2/1,081 = 0.0018501. واحتمال الحصول على 3 من 10 هو combin(10,3)×0.0018501 3 ×(1-0.0018501) 7 = 0.000000750178، أو 1 من 1,333,017.
تم خلط مجموعتين من أوراق اللعب (منها ورقتا جوكر) معًا. أُعطي لاعب نصفها. ما احتمال حصوله على جميع أوراق اللعب الحمراء الأربعة؟
هناك أربع بطاقات ثلاثية حمراء و١٠٤ بطاقات أخرى. هناك طريقة واحدة فقط للحصول على جميع البطاقات الثلاثية الحمراء الأربع. هناك مجموع (١٠٤،٥٠) = ١٫٤٦٦٩١ × ١٠، أي ٢٨ طريقة يمكن للاعب من خلالها الحصول على ٥٠ بطاقة من أصل ١٠٤ بطاقات أخرى. العدد الإجمالي للمجموعات هو مجموع (١٠٨،٥٤) = ٢٫٤٨٥٧٨ × ١٠ ٣٠. مجموع (١٠٤،٥٠) / مجموع (١٠٨،٥٤) = ٠٫٠٥٩٠١٢.
إذا كنت لا ترغب في التعامل مع هذه الأعداد الكبيرة، فإليك حلاً بديلاً. رتّب البطاقات الثلاث الحمراء الأربع من 1 إلى 4. احتمال وجود البطاقة الثلاث الحمراء الأولى في كومة اللاعب هو 54/108. الآن، احذف البطاقات الثلاث الأولى. احتمال حصول اللاعب على البطاقة الثلاث الحمراء الثانية هو 53/107، لأن لديه 53 بطاقة متبقية، ويتبقى 107 بطاقات. وبالمثل، احتمال حصول اللاعب على البطاقة الثلاث الحمراء الثالثة هو 52/106، والبطاقة الثلاث الحمراء الرابعة هو 51/105. (54/108) × (53/107) × (52/106) × (51/105) = 0.059012.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
في عمودك بتاريخ ١٤ ديسمبر ٢٠١٠، كتبتَ أن اليد AAAAAKK، المذكورة تحديدًا في أسلوب الكازينو، ربما لم تحدث قط في تاريخ اللعبة. ووفقًا لتاجر آخر، حصل لاعب على هذه اليد في محطة مين ستريت في نوفمبر ٢٠١٠.
مثير للاهتمام. كما كتبتُ، أقدّر أن هذه الظاهرة ستحدث مرة كل ٢٣.٧ عامًا تقريبًا في أي مكان في نيفادا. أعتقد أن تلك كانت إحدى تلك المرات.
لنفترض أنك اخترت رتبتين، مثلاً ملك وملكة. ما احتمال أن يكون ملك وملكة متجاورين، ولو لمرة واحدة على الأقل، في مجموعة أوراق لعب من 52 ورقة تم خلطها عشوائياً؟
حصلت على ٤٨٫٦٢٧٩٪. إذا كنت ترغب في المراهنة عليه، فإن احتمالات "نعم" ستكون ١٫٠٥٦٤ إلى ١.
سمعتُ مؤخرًا عن لعبة بريدج "مثالية"، حيث يحصل كل لاعب على ١٣ بطاقة من إحدى المجموعات الأربع. ما احتمالات ذلك؟
هناك أيضًا شائعات حول حدوث ذلك في لعبة الورق في وارويكشاير عام 2011. ولصالح القراء الآخرين، هذا السؤال هو ما هو احتمال تقسيم مجموعة من 52 بطاقة إلى أربع مجموعات من 13 بطاقة في كل منها، حيث تتكون كل مجموعة بالكامل من 13 بطاقة من إحدى البذلات.
هناك طريقة مُمكنة لترتيب 52 بطاقة في أربع مجموعات من 13 بطاقة، وهي الجمع (combin(52,13)*الجمع (combin(39,13)*الجمع (combin(26,13)) = 53,644,737,765,488,800,000,000,000,000. 4! = 24 هو عدد المجموعات الرابحة، إذ يُمكنك توزيع المجموعات الأربع على اللاعبين الأربعة بالطريقة التي تُريدها. لذا، فإن الاحتمالات تساوي 1 من 2,235,197,406,895,370,000,000,000,000. ولتوضيح هذا الرقم، إذا وزّع جميع سكان الأرض، البالغ عددهم 7.5 مليار نسمة، أوراق لعب بمعدل ورقة لعب واحدة في الثانية، فإن احتمال أن يُوزّع شخص ما ما يُسمى باليد المثالية قبل انفجار الشمس بعد 5 مليارات سنة هو 1 من 16,558.
ومع ذلك، يُعرّف البعض اليد "المثالية" بأنها حصول لاعب واحد على جميع البطاقات الـ ١٣ من أي نوع. أُبيّن أن احتمالية ذلك هي ١ من ٣٩,٦٨٨,٣٤٧,٤٩٧ لعبة. من المُرجّح أن يحدث هذا أحيانًا في مكان ما على الأرض.
ما هو احتمال أن يكون لدى لاعبين اثنين مجموعة واحدة في نفس اليد في لعبة تكساس هولدم مع استخدام كل منهما لكلا بطاقتيهما المخفيتين؟
أولاً، لنحدد عدد مجموعات بطاقات اللاعب واللوحة التي يُمكن أن يحدث فيها هذا. بالطبع، هناك أربع مجموعات. ثم هناك combin(13,4)=715 طريقة لاختيار أربع بطاقات من أصل 13 من المجموعة المُعطاة.
ثانيًا، إحدى طرق تحقيق ذلك هي استخدام ثلاث بطاقات من نفس النوع على اللوحة، واثنتين أخريين من بين 39 بطاقة أخرى. هناك 84 طريقة لاختيار ثلاث بطاقات من أصل 9 بطاقات متبقية من النوع المختار على اللوحة. ثم هناك 741 طريقة لاختيار بطاقتين إضافيتين من بين 39 بطاقة أخرى من الأنواع الثلاثة الأخرى. إذن، هناك 84 × 741 = 62,244 طريقة لاختيار ثلاث بطاقات من النوع المعني على اللوحة.
ثالثًا، هناك طريقة أخرى يمكن أن يحدث بها هذا وهي باستخدام أربع بطاقات من نفس النوع التي يمتلكها اللاعبون على اللوحة والبطاقة الأخرى من بين 39 بطاقة أخرى. هناك combin(9,4)=126 طريقة يمكن أن تحتوي بها اللوحة على أربع بطاقات من أصل 9 بطاقات متبقية من النوع المختار. ثم هناك 39 طريقة لاختيار بطاقة أخرى من بين 39 بطاقة أخرى في الأنواع الثلاثة الأخرى. ومع ذلك، لن تؤدي كل هذه الطرق إلى استخدام كلا اللاعبين لكلا البطاقتين المخفيتين. لكي يتحقق هذا الشرط، يجب أن تكون أقل بطاقة في النوع المعني موجودة على اللوحة. احتمال ذلك، من بين 8 بطاقات من نفس النوع قيد اللعب، هو 4/8 = 1/2. لذا، هناك 126*39*(1/2)=2457 طريقة مع وجود أربع بطاقات من النوع المعني على اللوحة.
رابعًا، آخر طريقة ممكنة لتحقيق ذلك هي وجود خمس بطاقات من نفس النوع على اللوحة. هناك 126 طريقة للحصول على خمس بطاقات من أصل تسع بطاقات متبقية من النوع المختار. مع ذلك، لن يؤدي كل هذا إلى استخدام كلا اللاعبين للبطاقتين المخفيتين. لتحقيق هذا الشرط، يجب أن تكون أقل بطاقتين من النوع المعني على اللوحة. احتمال ذلك، من بين 9 بطاقات من نفس النوع في اللعبة، هو 10/36 = 5/18. إذن، هناك 126*(5/18) = 35 طريقة للحصول على أربع بطاقات من النوع المعني على اللوحة.
وبالتالي، فإن عدد التركيبات التي سيحدث فيها هذا هو 715*(62,244 + 2,457 + 35) = 46,286,240.
العدد الإجمالي لمجموعات الطرق لاختيار أربع بطاقات للاعب من بين 52 بطاقة مخفية ثم 5 بطاقات أخرى من بين 48 بطاقة متبقية على اللوحة هو combin(52,4)*combin(48,5) = 463,563,500,400.
وبالتالي، فإن الاحتمال هو 46,286,240 / 463,563,500,400 = 0.000399395 = 1 في 2,504.
تم طرح هذا السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .
يعمل موزع كازينو على نسخة جديدة من لعبة بوكر الثلاث أوراق. يأخذ جميع الأوراق ذات الوجوه من مجموعة أوراق قياسية ويخلطها جيدًا. ثم يوزع ثلاث أوراق على اللاعب رقم 1، وثلاث أوراق على اللاعب رقم 2، وثلاث أوراق على اللاعب رقم 3، والأوراق الثلاث الأخيرة على اللاعب رقم 4. ما احتمال أن تحتوي جميع الأيدي الأربع على ستريت (JQK من أي نوع)؟
وزّع على لاعب واحد في كل مرة. احتمال حصول اللاعب الأول على واحدة من كل رتبة هو 4^3/مجموعة(12,3) = 64/220.
بافتراض حصول اللاعب الأول على ستريت، يتبقى في المجموعة ثلاث بطاقات من كل رتبة. احتمال حصول اللاعب الثاني على بطاقة واحدة من كل رتبة هو 3^3/comb(9,3) = 27/84.
بافتراض حصول أول لاعبين على ستريت، يتبقى في المجموعة ورقتان من كل رتبة. احتمال حصول اللاعب الثالث على ورقة واحدة من كل رتبة هو 2^3/comb(6,3) = 8/20.
بافتراض حصول اللاعبين الثلاثة الأوائل على ستريت، تبقى مجموعة أوراق ناقصة من كل رتبة. هذه الأوراق الثلاث تُشكّل ستريت بالطبع.
وبالتالي، فإن احتمال حصول جميع اللاعبين الأربعة على سلسلة متتالية هو (64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3.74%.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas، بدءًا من هذه التدوينة .
لنفترض أن لديّ مجموعة أوراق لعب من ٤٨ ورقة، أربع مجموعات، اثني عشر ورقة من كل مجموعة. إذا سحبت ١٥ ورقة، فما احتمال سحب ورقة واحدة على الأقل من كل مجموعة؟
لنبدأ بـ 100% ونطرح الاحتمالات التي تؤدي إلى أقل من أربع بدلات.
ما احتمال عدم احتواء الـ ٤٨ بطاقة على قلب، على سبيل المثال؟ هناك ٣٦ بطاقة ليست قلبًا. عدد طرق اختيار ١٥ بطاقة من أصل ٣٦ هو combin(٣٦، ١٥) = ٥,٥٦٧,٩٠٢,٥٦٠. عدد طرق اختيار ١٥ بطاقة من أصل ٤٨ هو ١,٠٩٣,٢٦٠,٠٧٩,٣٤٤. لذا، فإن احتمال عدم احتواء ١٥ بطاقة على قلب هو ٥,٥٦٧,٩٠٢,٥٦٠ / ١,٠٩٣,٢٦٠,٠٧٩,٣٤٤ = ٠.٠٠٥٠٩٣.
الآن، دعنا نضرب ذلك في أربعة، للحصول على احتمال تفويت أي نوع، وليس القلوب فقط: 4 × combin(36,15)/combin(48,15) = 0.02037174.
مع ذلك، يُحسب هذا مرتين في بعض الحالات. لنفترض أن لدينا ١٥ بطاقة سوداء. سيؤدي ذلك إلى حذف كلٍّ من القلوب والماس. سنحسب هذه الحالة مرتين. لذا، علينا تصحيح ذلك. هناك combin(4,2) = ٦ طرق لاختيار نوعين من أصل أربع بطاقات. احتمال أن تكون جميع البطاقات الـ ١٥ من أي نوعين محددين هو combin(24,15)/combin(48,15) = ١٣٠٧٥٠٤/١,٠٩٣,٢٦٠,٠٧٩,٣٤٤ = ٠.٠٠٠٠١٢٠. كما ذكرنا، هناك ست طرق لاختيار نوعين من أصل أربع بطاقات، لذا فإن عدد الطرق التي ستكون بها جميع البطاقات من نوعين هو ٦ × combin(24,15)/combin(48,15) = ٠.٠٠٠٠٧١٨.
بطرح ما حسبناه مرتين، نحصل على احتمال تمثيل بدلتين أو ثلاث بدل من 0.02037174 - 0.00000718 = 0.02036456.
لاحظ أننا لسنا بحاجة إلى القلق بشأن تمثيل بدلة واحدة، لأنه من المستحيل اختيار 15 بطاقة من أصل 12.
كخطوة أخيرة، اطرح احتمال وجود 2 أو 3 بدلات من 100% للحصول على احتمال تمثيل جميع البدل الأربع: 1.00000000 - 0.02037174 = 0.97963544.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
إذا قمت بتوزيع 13 بطاقة من مجموعة بطاقات مختلطة (من المفترض أنها عشوائية)، فكم عدد الرتب المختلفة التي يجب أن أتوقع رؤيتها؟
هذه مشكلة من نوع سلسلة ماركوف إذا كان هناك واحدة على الإطلاق.
يوضح الجدول التالي عدد الرتب المتوقعة من 0 إلى 4 بطاقات لجميع أعداد البطاقات الموزعة من 1 إلى 52.
الرتب المتوقعة حسب البطاقات الموزعة
| بطاقات | 0 رتبة | 1 رتبة | 2 رتب | 3 رتب | 4 رتب | مُتوقع الرتب |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0.058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0.169412 | 0.002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0.324994 | 0.009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0.519088 | 0.022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0.745498 | 0.044178 | 0.000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0.075630 | 0.001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0.003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0.173445 | 0.006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0.324850 | 0.015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0.422569 | 0.023770 | 8.611525 |
| 13 | 3.949628 | 5.705018 | 2.775414 | 0.535606 | 0.034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0.664202 | 0.048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0.065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0.968067 | 0.087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0.146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0.186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0.232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0.287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0.351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0.983193 | 3.775462 | 5.009748 | 2.721345 | 0.510252 | 12.016807 |
| 25 | 0.842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 26 | 0.717887 | 3.246098 | 5.072029 | 3.246098 | 0.717887 | 12.282113 |
| 27 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0.842737 | 12.392557 |
| 28 | 0.510252 | 2.721345 | 5.009748 | 3.775462 | 0.983193 | 12.489748 |
| 29 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 30 | 0.351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0.287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 32 | 0.232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0.186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 34 | 0.146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 35 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 36 | 0.087395 | 0.968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 37 | 0.065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 38 | 0.048067 | 0.664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 39 | 0.034334 | 0.535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0.023770 | 0.422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0.015846 | 0.324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 42 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0.006050 | 0.173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 44 | 0.003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0.001681 | 0.075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0.000720 | 0.044178 | 0.745498 | 4.373589 | 7.836014 | 12.999280 |
| 47 | 0.000240 | 0.022569 | 0.519088 | 3.893157 | 8.564946 | 12.999760 |
| 48 | 0.000048 | 0.009220 | 0.324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0.002353 | 0.169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0.058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
تحداني أحدهم بالرهان التالي. عليّ اختيار أي ثلاث رتب من أوراق البوكر القياسية، وكتابة توقعي، مع إخفائه حتى النهاية. على سبيل المثال، 7-آس-2. ثم عرض عليّ أن يراهن بمبلغ متساوٍ على أنه يستطيع تسمية رتبة واحدة على الأقل من رتبتي إذا حصل على ثلاث تخمينات. ما هي احتمالات فوزي؟
للفوز، يجب أن يكون توقع خصمك خاطئًا في جميع التنبؤات الثلاثة. احتمال خطأ التوقع الأول هو ١٠/١٣، واحتمال خطأ التوقع الثاني هو ٩/١٢، لأننا نستطيع استبعاد أول رتبة مُخمَّنة من الاحتمالات. احتمال خطأ التوقع الثالث هو ٨/١١، لأننا نستطيع استبعاد أول رتبتين مُخمَّنتين من الاحتمالات.
يجب أن تتحقق هذه الأمور الثلاثة جميعها للفوز. وبالتالي، فإن احتمالات فوزك هي (١٠/١٣) * (٩/١٢) * (٨/١١) = ٧٢٠/١٧١٦ = ٤١٫٩٦٪.
في حالة المال المتساوي، فإن ميزة المنزل في هذا الرهان، من جانبك، هي 16.08% (آه!).
تم اقتباس هذا السؤال من كتاب الرهانات المقترحة من تأليف أوين إيشيا (رقم 7).
تحداني أحدهم في رهان على أنه يستطيع الحصول على ١٢ نتيجة باستخدام نردين خلال ٢٧ رمية. لو لم يفعل، لكنت ربحت مبلغًا متساويًا. بما أن احتمال الحصول على ١٢ هو ١/٣٦، ألا يجب أن يحتاج ٣٦ رمية في المتوسط للحصول على ١٢؟ يبدو أن الاحتمالات كانت في صالحي لو أن خصمي حصل على ٢٧ رمية فقط. هل أنا محق، أم أين الخطأ في حساباتي؟
متوسط وقت الانتظار بين رميات الـ ١٢ هو ٣٦ رمية، بما في ذلك رمية الـ ١٢ نفسها. مع ذلك، هذا لا يعني أنها تأتي كل ٣٦ رمية بالضبط. احتمال عدم ظهور ١٢ هو (٣٥/٣٦). واحتمال عدم ظهوره بعد ٢٧ رمية هو (٣٥/٣٦)^٢٧. لذا، فإن احتمال ظهور ١٢ على الأقل هو ١-(٣٥/٣٦)^٢٧ = ٥٣.٢٦٪.
يوضح الجدول التالي احتمالية الحصول على ١٢ على الأقل من ٢٠ إلى ٣٦ رمية. تجدر الإشارة إلى أن الحصول على ٢٥ رمية ضروري لتحقيق أفضلية عند تساوي قيمة العملة.
الاحتمال 12
| لفات | احتمال |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |
نحن نعلم أن هناك combin(52,5)=2,598,960 تركيبة ممكنة لخمس بطاقات من أصل 52. سؤالي هو كم عدد الأيدي المكونة من خمس بطاقات والتي يمكن الحصول عليها من مجموعة مكونة من خمس مجموعات؟
دعونا نأخذ هذا النوع من اليد في كل مرة.
- خمسة من نفس البطاقة: يوجد 52 بطاقة مختلفة في المجموعة، لـ 52 تركيبة.
- أربع بطاقات متشابهة: هناك ٥٢ بطاقة محتملة للأربع بطاقات المتشابهة، و٥١ بطاقة للبطاقة المفردة. إذن، هناك ٥٢ × ٥١ = ٢٦٥٢ تركيبة محتملة لأربع بطاقات متشابهة.
- ثلاث بطاقات من نفس البطاقة واثنتان من بطاقة أخرى: هناك ٥٢ بطاقة محتملة للبطاقات الثلاث المتشابهة و٥١ بطاقة محتملة للزوج. إذن، هناك ٥٢ × ٥١ = ٢٦٥٢ تركيبة محتملة لبيت كامل.
- ثلاث بطاقات متشابهة وبطاقاتان فرديتان مختلفتان: هناك 52 بطاقة محتملة متشابهة، ومجموع (51،2) = 1,275 للبطاقات الفردية. إذن، هناك 52 × 1,275 = 66,300 تركيبة محتملة لثلاث بطاقات متشابهة.
- زوجان من نفس البطاقة وبطاقة مفردة واحدة: هناك 1,326 تركيبة ممكنة للبطاقات المختلفة التي تُشكّل أزواجًا. يتبقى 50 تركيبة للبطاقة المفردة. إذن، هناك 1,326 × 50 = 66,300 تركيبة ممكنة للزوجين.
- زوج واحد من نفس البطاقة وثلاث بطاقات فردية: هناك 52 بطاقة محتملة لهذا الزوج. ثم هناك combin(51,3)=20,825 طريقة لاختيار 3 بطاقات من أصل 51 بطاقة متبقية للبطاقات الفردية. إذن، عدد مجموعات البطاقات الفردية هو 52 × 20,825 = 1,082,900.
- خمسة بطاقات فردية: هناك combin(52,5)=2,598,960 طريقة لاختيار خمس بطاقات من أصل 52.
مجموع كل هذه التركيبات هو 3,819,816.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .


