احتمال - عملات معدنية
إذا تم رمي العملة المعدنية 1000 مرة، ما هو احتمال أن يقع العدد الإجمالي للرؤوس في نطاق من 452 إلى 548؟
في هذه المسألة، يمكننا استخدام التقريب الطبيعي للتوزيع ذي الحدين. تباين عدد الرؤوس هو 1000*(1/2)*(1/2)=250. وبالتالي، فإن الانحراف المعياري هو 250 1/2 = 15.8114. احتمال أن يكون عدد الرؤوس أقل من 548 هو normdist((548+0.5-500)/15.8114) = 0.998920، حيث normsdist هي دالة Excel لاحتمال وقوع متغير عشوائي بتوزيع طبيعي متوسطه 0 وانحراف معياري 1 تحت الدرجة Z المعطاة. بعد ذلك، نطرح احتمال أن يكون عدد الرؤوس أقل من 452. هذا هو normdist((452-0.5-500)/15.8114) = 0.001080. إذن، الإجابة هي 0.99892-0.00108 = 0.997840. مرة أخرى، هذا تقريب. الإجابة الفعلية هي ٠٫٩٩٧٨٥٦، لكن استنتاجها أصعب. في المتوسط، بعد تحديد نقطة في لعبة الكرابس، كم مرة سوف يحقق اللاعب هذه النقطة؟
إذا كانت نقطةٌ ما قد تم تحديدها في ٥/١٢ من المرات، فستكون ٦ أو ٨، و٤/١٢ لـ ٥ أو ٩، و٣/١٢ لـ ٤ أو ١٠. احتمال الحصول على ٦ أو ٨ هو ٥/١١، و٥ أو ٩ هو ٤/١٠، و٤ أو ١٠ هو ٣/٩. لذا، فإن احتمال الحصول على نقطة، بشرط تحديدها، هو: (٥/١٢)*(٥/١١)+(٤/١٢)*(٤/١٠)+(٣/١٢)*(٣/٩) = ٤٠.٦١٪.
يا سيد ساحر، إذا رمى ٥٠ شخصًا عملة معدنية في الهواء ٨ مرات مختلفة، فما نسبة من سيرمونها ٨ مرات متتالية؟ شكرًا لك مقدمًا.
احتمالية ظهور ثمانية نردات (صورة أو كتابة) لأي شخص هي 2 × (½) 8 = 1 من 128. إذا فعل 50 شخصًا ذلك، فسيحصل 0.39 منهم في المتوسط على جميع النردات (صورة أو كتابة). واحتمالية ظهور نرد واحد على الأقل هي 32.44%.
لديّ كيسٌ به مئة عملة، إحداها ذات وجهين. اخترتُ عملةً عشوائيًا، ثم لاحظتُ أنها انقلبت عشرةً متتاليةً على شكل وجهين. ما احتمال أن أكون قد اخترتُ العملة ذات الوجهين؟
هذا سؤالٌ في الاحتمالية الشرطية البايزية من الكتب المدرسية. عمومًا، احتمال A مع B هو احتمال A وB مقسومًا على احتمال B. في هذه الحالة، يرمي A العملة المعدنية ذات الوجهين 10 مرات متتالية، ويختار B العملة المعدنية ذات الوجهين. احتمال A وB هو 1/100. هذا لأن احتمال اختيار العملة المعدنية ذات الوجهين هو 1 من 100، وإذا حدث ذلك، فإن احتمالية رمي العملة المعدنية ذات الوجهين 100% هي 100%. احتمالية رمي العملة المعدنية ذات الوجهين 10 مرات متتالية، بافتراض اختيار عملة عشوائيًا، هي (1/100)*1 + (99/100)*(1/2) 10 . ذلك لأن هناك احتمالًا بنسبة 1% لاختيار العملة ذات الوجهين، والتي لديها احتمال 100% للحصول على 10 صور، واحتمالًا بنسبة 99% لاختيار عملة عادلة، والتي لديها احتمال (نصف) 10 للحصول على 10 صور متتالية. لذا، فإن احتمال اختيارك للعملة ذات الوجهين، بشرط أن تكون قد ألقيت 10 صور متتالية، هو 0.01/(0.01*1 + 0.99* 0.000977) = 0.911843.
هل لديك أي نصيحة للمراهنة على رمي العملة المعدنية؟
نعم! نصيحتي هي المراهنة على الوجه المكشوف عند بداية الرمية. وفقًا لموقع ساينس نيوز أونلاين، فإن احتمال سقوط العملة المعدنية على نفس الوجه الذي بدأت منه هو ٥١٪. يذكر المقال أن السبب هو أن العملة المعدنية المقلوبة لا تدور بدقة حول محورها، وأحيانًا تبدو وكأنها تنقلب بينما هي في الواقع ليست كذلك. تنطبق هذه الفرضية فقط إذا علقت العملة المعدنية في راحة اليد، لذا فإن ارتدادها ليس مشكلة. يذكر المقال أيضًا أن البنس الدوار سيسقط على الكتابة في ٨٠٪ من الحالات، نظرًا لأن جانب الصورة الأثقل يميل نحو السقوط أولاً. مع ذلك، لديّ شكوك حول هذا. لقد جربت هذا ٢٠ مرة وحصلت على ١١ صورة و٩ كتابة. احتمال الحصول على ٩ كتابة أو أقل في ٢٠ دورة مع احتمال نجاح ٨٠٪ هو ١ من ١٧٧٥.
أعتقد أنني قد وجدتُ إجابةً لمشكلة دوران البنس. قبل أكثر من عقد، أنجزتُ مشروعًا علميًا حول دوران البنس في الصف السادس الابتدائي. قرأتُ في مجلة أومني أن تدوير البنس بسرعة كبيرة يُؤدي غالبًا إلى إيقاف ظهور الكتابة لأن الجوانب تميل نحو الصورة. جربتُ ذلك مئات المرات وحصلتُ على نتائج شبه محايدة، باستثناء مرتين عندما وقف البنس على حافته.
بعد ساعات طويلة من العمل، اكتشفتُ أخيرًا أنني كنتُ أدورها بسرعة كبيرة، ودرتُها ببطءٍ أكبر من اللازم، فأعطاني الدورانُ الأبطأُ النتيجةَ المرجوة، أي الكتابة لأعلى. كما أن البنس ليس متساويًا تمامًا، وبدا أن بدء الدوران على الجزء الأرفع زاد من تماسكه. بعض المخططات المليئة بالمعلومات غير الدقيقة ودائرة كرتونية عملاقة مزينة مثل البنس، منحتني درجةً ممتازةً في العلوم، ورسوبًا في جميع المواد الأخرى، لأنني تجاهلتُ جميع واجباتي المنزلية.
لقد أثبت بشكل قاطع من خلال تجربة بسيطة أجريت منذ أكثر من عشر سنوات، والتي بالكاد أتذكر أي شيء عنها، ولم يكن لدي أي فهم حقيقي لما كنت أفعله في ذلك الوقت، أنك ربما كنت تدير قرشًا بسرعة كبيرة جدًا.
حسنًا، حاولتُ ذلك مجددًا، حيثُ أدرتُ العملة المعدنية ببطء مئة مرة. أعني ببطء أن الوقت بين نقرها وظهور النتيجة كان ثانيتين على الأقل، ولكن أقل من خمس ثوانٍ. استخدمتُ عملة معدنية لامعة من طراز 2004-D. كانت نتائجي 52 صورة و48 كتابة. لذا، ما زلتُ غير مقتنع بأن دوران العملة المعدنية بأي سرعة يُعطي نتائج عكسية.
أفهم أن "وقت الانتظار" لحدث ما هو مقلوب احتمال وقوعه. أرغب في حساب وقت الانتظار للحصول على رقم 2 متتالي باستخدام حجر نرد واحد. في محاكاة، أحصل على 42 رمية في المتوسط. كيف أربط ذلك باحتمال الحصول على رقم 2 متتالي؟
صحيح أنه في حالة الأحداث الفردية، إذا كان الاحتمال p، فإن متوسط وقت الانتظار هو 1/p. لكن الأمر يزداد تعقيدًا مع الأحداث المتتالية. لنفترض أن x هي الحالة التي لم تكن فيها آخر رمية 2. هذه هي الحالة أيضًا في البداية. لنفترض أن y هي الحالة التي كانت فيها آخر رمية 2. بعد الرمية الأولى، هناك احتمال 5/6 أن نبقى في الحالة x، واحتمال 1/6 أن نكون في الحالة y. لنفترض أن Ex(x) هو العدد المتوقع للرميات من الحالة x، وأن Ex(y) هو العدد المتوقع من الحالة y. إذًا...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y)، و
Ex(y) = 1 + (5/6)*ex(x)
حل هاتين المعادلتين...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
Ex(x) = 36*(7/6) = 42
وبالتالي فإن متوسط وقت الانتظار للحصول على اثنين متتاليين هو 42 لفة.
لدي نفس النوع من المشكلة، فقط من المتوقع أن تحصل على رأسين، في موقعي لمشاكل الرياضيات ، انظر المشكلة 128.
لنفترض أن لدينا لعبة قمار. عُرضت عملة معدنية غير متحيزة بشكل متكرر. في كل رمية، علينا دفع روبية واحدة. هناك نتيجتان محتملتان: H أو T. إذا أصبح الفرق بين رمية الرأس ورمية الكتابة 3، فسنحصل على 8 روبيات من المقامر. هل يجب أن نلعب اللعبة، ولماذا؟ ما هو احتمال فوزنا؟ ما الذي يجب أن يؤثر على احتمال الفوز عندما نحصل على 7 أو 9 روبيات؟
دعونا نطلق على x عدد التقلبات المتوقعة من نقطة البداية.
دعونا نسمي y عدد التقلبات المتبقية المتوقعة إذا كان أحد الجانبين هو تقلب واحد في الأغلبية.
دعونا نطلق على z العدد المتوقع للتقلبات المتبقية إذا كان أحد الجانبين يحتوي على تقلبين في الأغلبية.
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
من السهل إذن، من خلال جبر المصفوفات، أن نلاحظ أن E(x) = 9، وE(y) = 8، وE(z) = 5. لذا، في المتوسط، سيستغرق الأمر 9 رميات ليصبح الفرق بين النقش والكتابة 3. لذا، عند 8 روبيات، يُعد هذا رهانًا جيدًا لمن يحصل على روبية واحدة في كل رمية، لأنه سيحصل في المتوسط على 9 روبيات، لكنه سيسدد 8 روبيات فقط. تبلغ نسبة ربح الكازينو للمقامر 11.11%. عند 9 روبيات، يُعد رهانًا عادلًا، أما عند 7 روبيات، فتبلغ نسبة ربح الكازينو 22.22%.
في مقالتك "اسأل الساحر" بتاريخ ١٣ مارس ٢٠٠٦ ، ذكرتَ ثلاث صيغ للعبة "الروبية". مع أن الحل صحيح رياضيًا، إلا أنني لا أستطيع فهم كيفية تمثيل المعادلات الثلاث للمسألة. هل يمكنكَ توضيح كيفية التوصل إلى هذه المعادلات الثلاث؟
طلب مني عدد من الأشخاص توضيح إجابتي. يتطلب الحل أساسيات جبر المصفوفات.
ابدأ بتعريف x على أنه الإجابة، أو متوسط عدد مرات الرمي حتى يصبح الفارق بين الوجه والكتابة 3.
ليكن y هو العدد المتوقع للانقلابات من نقطة يكون فيها أحد الجانبين لأعلى بمقدار انقلاب واحد.
ليكن z هو العدد المتوقع للانقلابات من نقطة يكون فيها أحد الجانبين لأعلى بمقدار انقلابين.
بعد التقليب الأول، يصبح أحد الجانبين هو الأغلبية بتقليب واحد. إذًا، x = 1 + y.
عندما يتقدم أحد الجانبين برمية واحدة، فإن رمية أخرى ستؤدي إما إلى التعادل الابتدائي، أو إلى تقدم أحد الجانبين برميتين. كلتا النتيجتين متساويتان في الاحتمال. إذًا، ص = ١ + ٠٫٥ × س + ٠٫٥ × ع.
عندما يتقدم أحد الجانبين برميتين، فإن رمية أخرى ستؤدي إلى تقدم أحد الجانبين برمية واحدة، أو نهاية اللعبة. مرة أخرى، كلا النتيجتين متساويتان في الاحتمال. إذًا، z=1+0.5*y
إذن لدينا ثلاث معادلات وثلاثة مجهولات:
(1) X=1+y
(2) Y = 1+ 0.5x + 0.5z
(3) Z = 1+ 0.5y
لحل هذه المسألة، دعونا أولاً نتخلص من الأعداد العشرية عن طريق ضرب المعادلتين الأخيرتين في 2.
(1) X=1+y
(2) 2Y = 2+ x + z
(3) 2Z = 2+ y
فلنستبدل 1+y، من (1) بـ x في (2).
2Y = 2 + 1 + y + z
(4) y = 3 + z
لا يوجد بديل لـ 3+z لـ y في (3)
2z = 2 + 3 + z
ز = 5
الآن استبدل 5 بـ z في (4) للحصول على
(5) ص = 3+ 5 = 8
لا يوجد بديل y = 8 في (1) للحصول على
(6) س = 9
يختار صديقي تسلسلًا من ثلاث رميات، إما صورة أو كتابة، ويمنحني خيار اختيار تسلسلي الخاص (المختلف). نرمي عملة عادلة عدة مرات حسب الحاجة حتى تظهر إحدى تسلسلاتنا. إذا اختار هو HHH، فأي تسلسل أختار؟ وما هي ميزتي في هذا الرهان؟ كيف أحسب التسلسل الذي أختاره بناءً على التسلسل الذي اختاره؟
يوضح الجدول التالي احتمال فوز اللاعب أ وفقًا لجميع الأنماط الممكنة المختارة للاعب أ واللاعب ب.
احتمال فوز اللاعب أ
| اللاعب أ | اللاعب ب | |||||||
| ههه هه | اتش اتش تي | هـ تـهـ | إتش تي تي | تي اتش اتش | تي اتش تي | تي تي اتش | تي تي تي | |
| ههه هه | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| اتش اتش تي | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| هـ تـهـ | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| إتش تي تي | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| تي اتش اتش | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| تي اتش تي | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| تي تي اتش | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| تي تي تي | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 | |
آلية الذاكرة لاختيار النمط الأمثل هي أن يكون اختياره الأول والثاني هو الثاني والثالث على التوالي. يجب أن يكون اختيارك الأول معاكسًا لاختيارك الثالث. على سبيل المثال، إذا اختار خصمك HTT، فيجب أن يكون اختيارك الثاني والثالث HT. اختيارك الأخير هو T، لذا يجب أن يكون اختيارك الأول H، لنمط HHT. باتباع هذه الاستراتيجية، سيكون احتمال فوزك من 2/3 إلى 7/8، حسب النمط الذي يختاره خصمك.
مرحباً، اسمي باتي. موقعك رائع، ويبدو أنك رجل واسع المعرفة. بالتأكيد هو الرجل الذي أرغب به في الكازينو! كنت أتساءل إن كان بإمكانك مساعدتي. أخبرت صديقي أنني سأبحث عن حل لمشكلة على الإنترنت. لو ساعدتني، لكان ذلك قد جعلني أبدو بمظهر جيد.
صديقي جامع عملات معدنية. اشترى كيسًا من بنسات القمح. أنا شخصيًا لا أعرف الكثير عن العملات المعدنية (وهو يُعلّمني مع مرور الوقت). لكنه قال إنه مندهش من عدم وجود سنة معينة في الكيس نظرًا لكثرة شيوعها. قال إن احتمال حدوث ذلك لا بد أن يكون مليارًا إلى واحد. أخبرته أنني سأحاول سؤال زملائي في مكتبي (الذين يدّعون أنهم عباقرة!)، وإذا لم يكونوا يعرفون، فسأحاول البحث قليلًا على الإنترنت. لقد صادفتك.
على أي حال، إذا استطعتَ المساعدة، سأكون ممتنًا للغاية. احتوت الحقيبة على حوالي 5,500 بنس. بلغ إجمالي بنسات القمح التي سكّتها جميع دور سك العملة الأمريكية 24,267,000,000 بنسة. بلغ عدد بنسات عام 1955 التي سُكّت (التي كان يبحث عنها) 330,000,000 بنسة. يقول بعض زملائي في مكتبي إن هناك عوامل أخرى، مثل التركيبة السكانية، وعدم توزيع دور سك العملة جميع البنسات، إلخ. ...................... أفترض أنهم على صواب، لكنني (وأنا متأكد من أن صديقي أيضًا) سأكتفي بمعرفة الاحتمالات التقريبية! أتمنى أن تتمكن من المساعدة.
أرقام سكّك قريبة من أرقام سكّ عملات ماونتن فيو . بافتراض أن كل بنس قمح سُكّ على الإطلاق له نفس احتمالية وجوده في الكيس، فإن احتمال ألا يكون أي بنس واحدًا من فئة 55 هو (24,267,000,000 - 330,000,000) / 24,267,000,000 = 0.986401286. يمكن تقريب احتمال ألا يكون 5500 عملة من فئة 55 تقريبًا إلى 0.986401286 5500 = 1 في 507,033,772,284,213,000,000,000,000,000,000,000.
والدي جامع عملات معدنية، لذا طلبت منه المساعدة في هذا الأمر. وهذا ما قاله:
هذا تخميني. في عام ١٩٥٥، سُكَّ عدد قليل من سنتات لينكولن في فيلادلفيا، وقد سُكَّ التاريخ مرتين. لا أحد يعلم عددها بالضبط. خُلطت هذه السنتات مع سنتات أخرى للتداول قبل اكتشاف الخطأ. تبلغ قيمة العينة غير المتداولة اليوم ما بين ٢٠٠٠ و٦٠٠٠ دولار أمريكي. أظن أن كيس "القمح" قد أُزيلت منه جميع سنتات عام ١٩٥٥ من قِبل شخص يبحث عن عينات مزدوجة القالب. إليكم صورة لأحدها: سنت واحد من عام ١٩٥٥، الوجه الآخر مزدوج القالب .
لاحظ أن هذا الموقع يبيع عملات "قمح"، ومن المؤكد أن بعض عمليات استبعاد التمور قد حدثت بالفعل بعد أن جمعها التاجر. كنت أظن أن عملات 1955 غير المصبوبة بالقالب المزدوج ستُعاد إلى المجموعة، ولكن ربما تُباع منفصلة أو تُصهر. النحاس المستخدم في بنسات القمح يساوي اليوم أكثر بكثير من سنت واحد. لهذا السبب تحولوا إلى سنتات الزنك المطلية بالنحاس قبل بضعة عقود. من المحتمل أن دار السك نفسها قررت عدم توزيع العديد من عملات 1955، وقامت بصهرها بعد سكها لتجنب التدافع المحموم على العملات النادرة المصبوبة بالقالب المزدوج. لطالما شعرت دار السك ومكتب البريد بالحرج من أخطاء الطباعة، ويحاولان منع تداولها.
في عمودك الأخير قلت أن "احتمالية أن 5500 عملة لا تكون 55 يمكن تقريبها بشكل وثيق للغاية على أنها 0.9864012865500 = 1 في 507،033،772،284،213،000،000،000،000،000،000."
أفترض أن هذا الرقم "تقريبي" نظرًا لتأثير الإزالة عند استخدام 5500 عملة. يا له من تأثير ضئيل للإزالة! هذا مثال جيد على انخفاض احتمالية الحصول على العملات المستهدفة عند إزالة العملات غير المستهدفة، لأن تأثير الإزالة ضئيل جدًا مقارنةً باحتمالية أكبر بكثير للعبة غير دقيقة، أي إزالة العملات المستهدفة.
نعم، قلتُ "تقريبًا" لأن عدد البنسات في العالم محدود. إذا أخرجتُ بنسة واحدة من غير فئة 55 من الكيس، فإنّ تأثير الإزالة يزيد من احتمال أن يكون كل بنسة أخرى في الكيس فئة 55. لو لم أقل "تقريبًا"، لكان ثلاثة أشخاص على الأقل قد كتبوا لي لتصحيحي. بالطبع، إنه تأثير ضئيل للغاية، لكن العديد من قرائي مثاليون، وسينقضون عليّ لأتفه الأسباب.
هناك طاولتان في غرفة. على الطاولة اليمنى ١٠٠ عملة، ٢٠ منها موجهة لحرف H، والباقي (٨٠) موجهة لحرف T. لا توجد عملات على الطاولة الأخرى. الهدف هو تحريك العملات بطريقة ما بحيث يكون هناك عدد متساوٍ من العملات موجهة لحرف H على كلا الطاولتين. لا يمكنك رؤية العملات (في الغرفة المظلمة) أو لمسها لمعرفة ما إذا كانت موجهة لأعلى أم لأسفل.
انتقل إلى موقعي الآخر، mathproblems.info للحصول على الحل (تحذير من المفسد!)
عرض عليّ صديقي أن يراهنني بمبلغ 20 دولارًا، وأن يعطيني احتمالًا بنسبة 3 إلى 1، فإذا رميتُ عملة معدنية 100 مرة، فستظهر 50 وجهًا و50 ظهرًا بالضبط. لو حدث ذلك، لربحتُ 60 دولارًا، وإن لم يحدث، فسأكون مدينًا له بـ 20 دولارًا. هل كان عليّ أن أقبل الرهان؟ أيضًا، إذا لم تكن النتيجة 50/50 هي الأرجح، فهل هناك نتيجة أخرى (مثل 51/49) أكثر احتمالًا؟
احتمال الحصول على 50 من كلٍّ منهما هو ناتج الجمع (100، 50) × (1/2) 100 = 7.96%. والاحتمالات العادلة هي 11.56 إلى 1. لذا، إذا كانت النسبة 3 إلى 1، فهذا رهان ضعيف، مع هامش ربح للكازينو بنسبة 68.2%. هذا ما لديك. نسبة 50/50 هي الأرجح بين ظهور الصورة والكتابة. ومن الرهانات المثيرة للاهتمام ما إذا كان عدد ظهور الصورة والكتابة سيقع بين 47 و53 أم لا. واحتمال الوقوع ضمن هذا النطاق هو 51.59%. إذا وجدتَ شخصًا يراهن على أن المجموع سيقع خارج هذا النطاق، فعند الرهان على رهان متساوٍ، ستكون لديك ميزة بنسبة 3.18%.
يوضح الجدول التالي احتمالية ظهور ما بين 30 إلى 70 رأسًا وظهرًا.
احتمال ظهور الوجه/الكتابة في 100 رمية
| رؤوس/ذيول | احتمال |
|---|---|
| 30، 70 | 0.000023 |
| 31، 69 | 0.000052 |
| 32، 68 | 0.000113 |
| 33، 67 | 0.000232 |
| 34، 66 | 0.000458 |
| 35، 65 | 0.000864 |
| 36، 64 | 0.001560 |
| 37، 63 | 0.002698 |
| 38، 62 | 0.004473 |
| 39، 61 | 0.007111 |
| 40، 60 | 0.010844 |
| 41، 59 | 0.015869 |
| 42، 58 | 0.022292 |
| 43، 57 | 0.030069 |
| 44، 56 | 0.038953 |
| 45، 55 | 0.048474 |
| 46، 54 | 0.057958 |
| 47، 53 | 0.066590 |
| 48، 52 | 0.073527 |
| 49، 51 | 0.078029 |
| 50 | 0.079589 |
الصيغة العامة لاحتمال فوز w من n محاولة، حيث احتمال كل فوز هو p، هي combin(n,w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw) .
إذا قمت برمي عملة معدنية 1000 مرة، ما هو احتمال أن أرى سلسلة من 10 صور أو كتب على التوالي؟
من الطريف أن تسأل؛ فقد أرسل لي قارئٌ آخر بحثًا أكاديميًا حول هذا الموضوع. يتضمن هذا البحث الرسم البياني التالي، الذي يُظهر أن الاحتمالية تبلغ حوالي 62%.
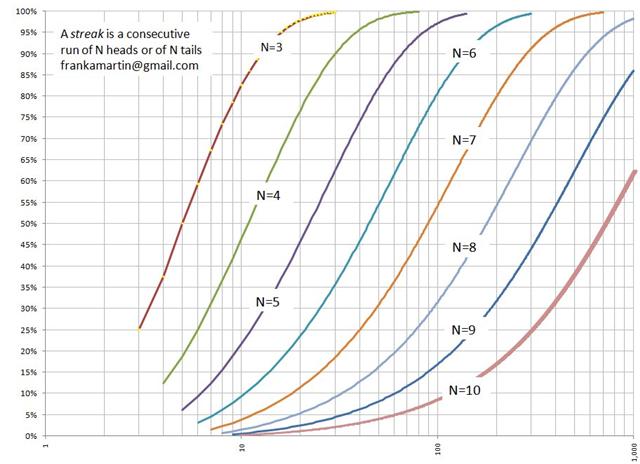
لمعرفة المزيد حول هذا الموضوع، يرجى زيارة ما هي احتمالات حدوث مثل هذه السلسلة الرهيبة في الكازينو؟ (483 كيلو بايت) بقلم فرانك مارتن.
إذا تم رمي العملة المعدنية 100 مرة، ما هو احتمال الحصول على سلسلة من 7 وجوه على التوالي على الأقل مرة واحدة على الأقل؟
إذا كان هناك تعبير سهل وغير متكرر للإجابة، فأنا لست على علم به. مع ذلك، هناك إجابة سهلة ومتكررة.
f(n)= pr(الذيل في التقلب الأول)×f(n-1) +
pr(الوجه في الرمية الأولى، الكتابة في الرمية الثانية)×f(n-2) +
pr(الوجه في أول رميتين، الكتابة في الرمية الثالثة)×f(n-3) +
pr(الوجه في أول 3 رميات، الكتابة في الرمية الثالثة) × f(n-4) +
pr(الوجه في أول 4 رميات، الكتابة في الرمية الرابعة) × f(n-5) +
pr(الوجه في أول 5 رميات، الكتابة في الرمية الخامسة) × f(n-6) +
pr(الوجه في أول 6 رميات، الكتابة في الرمية السادسة) × f(n-7) +
pr(الرؤوس في أول 7 تقلبات) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
أين:
f(n)=احتمال النجاح في غضون n تقلبات.
pr(x)=احتمال حدوث x.
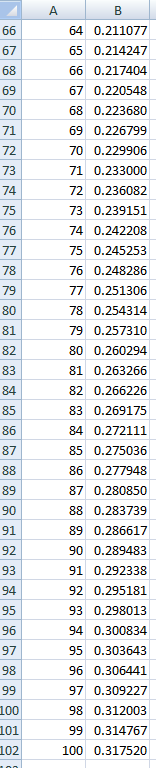
جداول البيانات مثالية لمثل هذه المسائل. في لقطات الشاشة لجدول البيانات أدناه، وضعتُ احتمالًا يساوي 0 للخلايا من B2 إلى B8، لأنه لا يمكن الحصول على 7 صور متتالية في 6 عمليات قلب أو أقل. بالنسبة للخلية B9، وضعتُ الصيغة التالية:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
ثم نسختها ولصقتها من الخلية B10 إلى الخلية B102، وهو ما يعادل 100 انعكاس. هذا الاحتمال هو 0.317520. وقد أكدته محاكاة عشوائية.
 |  |
بعد نشر هذا المقال، شاركني ريك بيرسي حله لجبر المصفوفات. إليكم الحل بكلماتي الخاصة. أفترض أن القارئ على دراية بأساسيات جبر المصفوفات.
أولاً، هناك ثماني حالات محتملة يمكن أن تكون فيها الزعنفة في أي نقطة:
p 1 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 7 رؤوس أخرى من النقطة الحالية.
p 2 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 6 رؤوس أخرى من النقطة الحالية.
ص 3 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 5 رؤوس أخرى من النقطة الحالية.
ص 4 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 4 رؤوس أخرى من النقطة الحالية.
ص 5 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى 3 رؤوس أخرى من النقطة الحالية.
ص 6 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى رأسين إضافيين من النقطة الحالية.
ص 7 = احتمال النجاح، مع الأخذ في الاعتبار أنك تحتاج إلى رأس واحد إضافي من النقطة الحالية.
ص 8 = احتمال النجاح، مع العلم أنك لا تحتاج إلى المزيد من الرؤوس = 1.
لنُعرّف الحد الأقصى للرقم S n بأنه احتمالية وجوده في كل حالة بعد الرمية رقم n. يمثل S 0 الاحتمالات قبل الرمية الأولى، حيث تكون نسبة وجوده في الحالة 0 100%. إذًا، S 0 =
| 1 0 0 0 0 0 0 0 |
دع T تكون مصفوفة التحويل من تقلبتين متتاليتين، أو S n إلى S n+1 ، حيث S n+1 = T × S n
- إذا كنت في الحالة 1، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 2 (مع وجود وجه)، وفرصة 0.5 للبقاء في الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 2، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 3 (مع وجود وجه)، وفرصة 0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 3، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 4 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 4، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 5 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 5، فبعد رمية واحدة لديك فرصة 0.5 لتكون في الحالة 6 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 6، فبعد رمية واحدة لديك فرصة 0.5 لوجودك في الحالة 7 (مع وجود وجه)، وفرصة 0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 7، فبعد رمية واحدة لديك فرصة 0.5 لتكون في الحالة 8 (مع وجود وجه)، و0.5 للعودة إلى الحالة 1 (مع وجود ظهر).
- إذا كنت في الحالة 8، فقد حققت النجاح، وستبقى في الحالة 8 باحتمالية 1.0.
وضع كل ذلك في شكل مصفوفة الانتقال T =
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
للوصول إلى احتمال كل حالة بعد قلب واحد...
(1) S 1 = S 0 × T
ماذا عن بعد الانقلابين؟
(2) S 2 = S 1 × T
دعونا نستبدل المعادلة (1) في المعادلة (2)...
(3) S 2 = S 0 × T × T = S 0 × T 2
ماذا عن بعد 3 تقلبات؟
(4) S 3 = S 2 × T
استبدال المعادلة (3) في (4)...
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
يمكننا الاستمرار في القيام بذلك حتى الوصول إلى الحالة التي نصل إليها بعد الانقلاب رقم 100...
S 100 = S 0 × T 100
إذن، ما هو T 100 ؟ قبل ظهور الحواسيب، كان من الصعب جدًا فهم هذه الأمور. مع ذلك، باستخدام دالة MMULT في برنامج Excel، ومع كثرة النسخ واللصق، نجد أن T 100 =
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
يوضح لنا المصطلح الموجود في أعلى اليمين احتمالية وجودنا في الحالة 8 بعد 100 عملية رمي، وهو 0.317520.
هل سمعتَ بقصة لاعب الكريكيت الأسترالي الذي أخطأ في قرعة عملة معدنية لـ 35 مباراة متتالية، قبل أن يُصيب في القرعـة السادسة والثلاثين؟ ما هي احتمالات حدوث ذلك؟
لم أكن قد سمعتُ بهذا حتى ذكرتَه. أنت تشير إلى القصة المذهلة للاعبة الكريكيت المراهقة كريستي بيرين ، لاعبة فريق ماغبايز، والتي أخطأت في رمي العملة 35 مرة متتالية. احتمال الحصول على 35 إجابة خاطئة أو أكثر هو (1/2) 35 = 1 من 34,359,738,368. ولتوضيح ذلك، فإن احتمال الحصول على باوربول هو 1 من 195,249,054. وهذا يزيد بـ 176 مرة عن احتمال إخفاق 35 رمية متتالية.
هل لديك أي نصيحة للمراهنة على رمي العملة المعدنية؟
نعم! راهن على الجانب المكشوف في يد اللاعب. خلصت الورقة البحثية الأكاديمية "التحيز الديناميكي في رمي العملة" التي أعدها بيرسي دياكونيس وسوزان هولمز وريتشارد مونتغمري إلى أن العملة ستستقر على نفس الجانب الذي بدأت منه في 51% من الحالات.
تم طرح هذا السؤال ومناقشته في منتدى موقعي المرافق Wizard of Vegas .
في المتوسط، كم عدد المحاولات اللازمة في مباراة متعادلة ٥٠/٥٠ لخسارة مباراتين متتاليتين؟ ماذا عن ٣، ٤، ن على التوالي؟
دعونا نحل حالة الخسارتين أولاً.
ليكن x هو العدد المتوقع للرميات المستقبلية بدءًا من البداية أو بعد أي فوز.
ليكن y هو العدد المتوقع للتقلبات المستقبلية بعد خسارة واحدة.
يمكننا إعداد المعادلتين التاليتين:
(1) x = 1 + .5x + .5y
يُمثل هذا أن على اللاعب رمي العملة لتغيير الحالة. هناك احتمال ٥٠٪ للفوز، والبقاء في الحالة س. وهناك احتمال ٥٠٪ للخسارة، والانتقال إلى الحالة ص.
(2) y = 1 + .5x
من الحالة y، يُمثل الرقم 1 رمية النرد عند هذه النقطة. احتمال الفوز 50%، والعودة إلى الحالة x. احتمال الخسارة 50%، مما يُنهي اللعبة، دون الحاجة إلى رميات إضافية، لذا يُفترض أن النتيجة 0.5*0.
اضرب المعادلتين في 2 ثم أعد ترتيبهما للحصول على:
(3) س - ص = 2
(4) -س + 2ص = 2
أضف المعادلتين للحصول على:
(5) ص = 4
أدخل ذلك في أي معادلة من (1) إلى (4) واحصل على x = 6.
بالنسبة لحالة الخسارة الثلاث، قم بتعريف الحالات الثلاث المحتملة على النحو التالي:
ليكن x هو العدد المتوقع للرميات المستقبلية بدءًا من البداية أو بعد أي فوز.
ليكن y هو العدد المتوقع للتقلبات المستقبلية بعد خسارة واحدة.
ليكن z هو العدد المتوقع للانقلابات المستقبلية بعد خسارتين.
المعادلات الأولية هي:
x = 1 + .5x + .5y
y = 1 + .5x + .5z
z = 1 + .5x
يمكننا إعداد الحالات الأولية في شكل مصفوفة على النحو التالي:
| 0.5 | -0.5 | 0 | 1 |
| -0.5 | 1 | -0.5 | 1 |
| -0.5 | 0 | 1 | 1 |
إذا كنت تتذكر جبر المصفوفة، يمكننا حل x على شكل محدد (A)/محدد (B) حيث
أ =
| 1 | -0.5 | 0 |
| 1 | 1 | -0.5 |
| 1 | 0 | 1 |
ب =
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
يحتوي إكسل على دالة مُحدِّدة مفيدة: =mdeterm(المدى). في هذه الحالة، x = mdeterm(المصفوفة أ)/mdeterm(المصفوفة ب) = 1.75/0.125 = 14.
يمكننا استخدام التكرار لخسائر متتالية إضافية. لنفترض أن الرقم 4. نعلم مما سبق أن الأمر يتطلب 14 رمية في المتوسط للحصول على 3 خسائر متتالية. عندها، ستُرمى العملة مرة أخرى، مع احتمال 50% للبدء من جديد. إذًا:
x = 14 + 1 + x/2
س/2 = 15
س = 30
بمعنى آخر، أضف واحدًا إلى الإجابة السابقة ثم ضاعفه.
ليس من الصعب ملاحظة النمط. العدد المتوقع للتقلبات للحصول على خسارة متتالية هو ٢ ن+١ -٢.
تم طرح هذا السؤال ومناقشته في منتدى Wizard of Vegas .
إذا تم رمي عملة معدنية عادلة n مرة، فما هو احتمال رؤية سلسلة واحدة على الأقل من العملات ذات النهاية الخلفية؟
الإجابة هي 1-F (t) n+2 /2 n ، حيث F (t) n هو الرقم n في متتالية فيبوناتشي ذات الخطوة t.
قد تتساءل ما هي متتالية فيبوناتشي؟ الرقم الأول هو واحد. في متتالية ذات خطوة t، كل رقم لاحق يساوي مجموع أرقام t السابقة. افترض أن أي رقم قبل الرقم الأول يساوي صفرًا.
لنلقِ نظرة على متتالية من خطوتين. الرقم الأول هو ١. الرقم الثاني هو مجموع الرقمين السابقين. بافتراض وجود صفر قبل الواحد، يكون الرقم الثاني ٠ + ١ = ١. الرقم الثالث ١ + ١ = ٢، الرقم الرابع ١ + ٢ = ٣، الرقم الخامس ٢ + ٣ = ٥.
الأرقام الاثني عشر الأولى من سلسلة فيبوناتشي المكونة من خطوتين هي: 1، 1، 2، 3، 5، 8، 13، 21، 34، 55، 89، 144.
لنأخذ مثالاً. ما احتمال ظهور وجهي كتابة متتاليين على الأقل مرة واحدة في كل عشر رميات؟
نستخدم متتالية فيبوناتشي ذات الخطوتين، لأننا نحتاج إلى طرفين فقط. العدد الثاني عشر في المتتالية (أكثر باثنين من عدد مرات قلب الورقة) هو ١٤٤. إذن، الإجابة هي ١-F (٢) ١٠ + ٢ / ٢ ١٠ = ١ - ١٤٤/٢ ١٠ = ١ - ١٤٤/١٠٢٤ = ٨٥٫٩٤٪.
ماذا عن احتمال الحصول على خمسة ذيول متتالية في العشرين رمية؟
أول 22 رقم فيبوناتشي من 5 خطوات هي 1، 1، 2، 4، 8، 16، 31، 61، 120، 236، 464، 912، 1793، 3525، 6930، 13624، 26784، 52656، 103519، 203513، 400096، 786568.
والإجابة هي 1 - F (5) 20+2 / 2 20 = 1 - 786,568 / 1,048,576 = 1 - 75.01% = 24.99%.
تمت مناقشة هذا السؤال في منتدياتي في Wizard of Vegas .
هناك عملة معدنية متحيزة، احتمال ظهور الصورة عليها هو 60%. تُقلب العملة حتى يظهر وجها الصورة أو الكتابة على التوالي. ما احتمال ظهور وجهي الصورة أولاً؟
وهنا الجواب والحل (PDF).
لمناقشة هذه المشكلة، يرجى زيارة منتدياتي في Wizard of Vegas .
أيها الساحر، أتحداك في رهان. إليك القواعد:
- اختر أي نمط تريده للرأس (H) والذيل (T). على سبيل المثال، HTT.
- بعد الكشف عن نمطك، سأختار نمطي.
- سنقلب العملة مرارًا وتكرارًا حتى يظهر نمط واحد بالترتيب. الفائز هو من يختار هذا النمط.
- سأعطيك احتمالات 3 إلى 2.
هل تقبل؟ سأفعل ذلك عدة مرات كما تريد.
لا، محاولة جيدة. اللاعب الثاني يتمتع بأفضلية موقعية كبيرة. إليك استراتيجية اللاعب الثاني واحتمال فوزه.
استراتيجية لعبة Odiusgambit
| اللاعب 1 | اللاعب 2 | اللاعب رقم 2 يفوز |
|---|---|---|
| ههه هه | تي اتش اتش | 87.50% |
| اتش اتش تي | تي اتش اتش | 75.00% |
| هـ تـهـ | اتش اتش تي | 66.67% |
| اتش اتش تي | تي اتش اتش | 75.00% |
| تي اتش اتش | إتش تي تي | 75.00% |
| تي اتش تي | تي تي اتش | 66.67% |
| تي تي اتش | إتش تي تي | 75.00% |
| تي تي تي | إتش تي تي | 87.50% |
كما يوضح الجدول أعلاه، فإن أفضل فرصة لي للفوز، أو أقلها لك، هي إذا اخترت إما THT أو HTH، حيث لا تزال فرصتي في الفوز 1 من 3 فقط. يجب أن أحصل على 2 إلى 1 حتى يكون رهانًا عادلاً، لذا فإن الحصول على 3 إلى 2 فقط يعني أن لديك ميزة بنسبة 16.67%.
إليك طريقة لتذكر استراتيجية اللاعب الثاني. ليكن P(x) هو اختيار اللاعب الأول للمركز x. وليكن O(x) هو عكس اختيار اللاعب الأول للمركز x. يجب على اللاعب الثاني دائمًا اختيار: O(2) - P(1) - P(2).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
إذا رميت عملة معدنية عادية 40 مرة، فما احتمال ظهور 5 صور و5 كتابات متتالية؟ "الصورة" تعني 1 على الأقل، و"5" تعني 5 على الأقل. ليس بالضرورة أن يكون خطا الصورة والكتابة متجاورين.
الرجاء الضغط على الزر أدناه للحصول على الإجابة.
الإجابة هي ١٠٧٬٠٩٤٬٥٤٨٬٢٢٥ / ٥٤٩٬٧٥٥٬٨١٣٬٨٨٨ = تقريبًا ١٩٬٤٨٠٤٪.وهنا الحل الخاص بي (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
قرر هنري وتوم المراهنة على رمي العملة. يفوز هنري على الصورة، ويفوز توم على الكتابة.
سعر الرمية دولار واحد، وقد شعروا بالملل الشديد، فقرروا القيام بمليون رمية. في نهاية الجلسة، سيحرر الخاسر شيكًا للفائز بالرصيد النهائي. ما هي القيمة المتوقعة لمبلغ الشيك؟
الصيغة العامة للإجابة هي sqrt(التباين * (2/pi)).
التباين في هذه الحالة هو ١٠٠٠٠٠٠. لذا، فإن الفرق المطلق المتوقع بين النتائج الفعلية والمتوقعة هو الجذر التربيعي (١٠٠٠٠٠٠ × (٢/باي)) = ~ ٧٩٧.٨٨٤٥٦٠٨٠٢٨٦٥٣٥٥٨٧٩٨٩٢١١٩٨٦٨٧٦٣٧٣٦٩٥١٧١٧٢٦ ٢٣٢٩٨٦٩٣١٥٣٣١٨٥١٦٥٩٣٤١٣١٥٨٥١٧٩٨٦٠٣٦٧٧٠٠٢٥٠٤٦٦ ٧٨١٤٦١٣٨٧٢٨٦٠٦٠٥١١٧٧٢٥٢٧٠٣٦٥٣٧١٠٢١٩٨٣٩٠٩١١١٦٧ ٤٤٨٥٩٩٢٤٢٥٤٦١٢٥١٠١٥٤١٢٦٩٠٥٤١١٦٥٤٤٠٩٩٨٦٣٥١٢٩٠٣ 269161506119450728546416733918695654340599837 28381269120656178667772134093073.
أطرح سؤالاً مرتبطًا في اسأل المعالج #358 ، والذي سيساعد في إظهار المكان الذي أحصل فيه على مصطلح sqrt(2/pi).
تم طرح هذا السؤال ومناقشته في المنتدى في Wizard of Vegas .
لنفترض أن كازينو لديه لعبة تعتمد على رمية عملة عادلة، ويدفع فيها مبلغ متساوٍ. يرغب لاعب في اللعب مليون مرة برهان دولار واحد. ما هو المبلغ الذي يجب أن يضعه في حسابه ليكون لديه فرصة 50% لتجنب الإفلاس؟
دعونا أولاً نجيب على السؤال حول احتمال أن يخسر اللاعب أكثر من x وحدات بعد مليون عملية رمي، على افتراض أن اللاعب لديه رصيد غير محدود.
بما أن هذا رهان عادل، فإن متوسط الربح بعد مليون رمية هو صفر. تباين كل رمية يساوي 1، لذا فإن تباين مليون رمية يساوي مليونًا. وبالتالي، فإن الانحراف المعياري الواحد يساوي sqrt(1,000,000) = 1000.
يمكننا حساب الرصيد المطلوب باستخدام دالة إكسل =norm.inv(الاحتمال، المتوسط، الانحراف المعياري). على سبيل المثال، إذا أدخلنا =norm.inv(.25,0,1000)، نحصل على -674.49. هذا يعني أنه بعد مليون رمية، يكون لدى اللاعب احتمال 25% أن يخسر 674 أو أكثر. يرجى العلم أن هذا تقدير. للحصول على إجابة صحيحة، يجب استخدام التوزيع الثنائي، وهو أمرٌ مُرهقٌ للغاية مع مليون رمية.
من المحتمل جدًا أن ينفد رصيد اللاعب قبل أن يُعرض المليون دولار إذا راهن بـ 674 دولارًا. إذا استمر في اللعب بالدين، فقد يتعافى وينتهي بخسارة أقل من 674 دولارًا. في الواقع، بمجرد أن يصل اللاعب إلى -674، هناك احتمال بنسبة 50/50 أن ينتهي به الأمر بخسارة أعلى أو أقل من -674 في أي وقت مستقبلًا.
لذا، إذا كان اللاعب قادرًا على اللعب بالائتمان، فهناك ثلاث نتائج محتملة.
- اللاعب لا ينخفض أبدًا إلى ما دون -674.
- ينخفض مستوى اللاعب إلى ما دون -674 في مرحلة ما، لكنه يتعافى وينتهي عند مستوى أعلى من -674.
- ينخفض مستوى اللاعب إلى ما دون -674 في مرحلة ما، ويستمر في اللعب ويخسر المزيد.
لقد حددنا السيناريو الثالث باحتمالية 25%.
يجب أن يكون السيناريو 2 بنفس احتمال السيناريو 3، لأنه بمجرد أن يكون اللاعب أقل من -674، تكون لديه فرصة 50/50 لإنهاء اللعبة أعلى أو أقل من تلك النقطة بعد مليون عملية قلب.
السيناريو 1 هو البديل الوحيد الآخر، والذي يجب أن يكون احتماله 100% - 25% - 25% = 50%.
إذا كان احتمال عدم هبوط اللاعب أبدًا إلى ما دون 674 هو 50%، فإن البديل للانخفاض إلى ما دون 674 يجب أن يكون 100% - 50% = 50%.
إذن، هذه إجابتنا على السؤال الأصلي، 674 دولارًا.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .


