احتمال - أسئلة عامة
هل أنت تقول أنه على المدى الطويل سوف تخسر في كل لعبة كازينو بغض النظر عما تفعله؟
باستثناء فرص التوقعات الإيجابية النادرة في لعبة البلاك جاك والفيديو بوكر، نعم، هذا ما أقوله.
كيف يمكنني تحويل الاحتمالات الخاصة بك إلى صيغة x إلى y؟
إن القول بأن احتمالات حدوث شيء ما هي س إلى ص يعني أن الحدث المعني سيقع س مرة مقابل كل ص مرة لا يقع فيها. لإجراء التحويل، لنفترض أن ص هو احتمال وقوع حدث ما. يمكن أيضًا التعبير عن الاحتمالات بـ (1/ص) -1 إلى 1. لنلقِ نظرة على مثال. احتمال سحب فل هاوس في لعبة ستاد بخمس بطاقات هو 0.00144058. ويمكن أيضًا تمثيل ذلك بـ 693.165 إلى 1.
كنتُ أشاهد مؤخرًا تجمعًا لكرة القدم. كان هذا التجمع عبارة عن شبكة من 100 مربع، والأرقام من 0 إلى 9 تمتد على محوري X وY، وتتوافق مع الرقم الأخير من النتيجة. لستُ من مشجعي كرة القدم، ولم أراهن على هذا التجمع، لكنني مقامر، ولا أعتقد أنه رهان جيد.
أفترض أنك تعرف نوع المجموعة التي أتحدث عنها. سعر كل صندوق ٥ دولارات، والمدفوعات تُدفع كل ربع سنة. إذا فاز صندوقك، فستربح ١٢٥ دولارًا، ومن الممكن الفوز بجميع الأرباع الأربعة إذا بقيت الأرقام الأخيرة كما هي، وستربح ٥٠٠ دولار، بنسبة ١٠٠ إلى ١.
كان الشخص الذي طلب الرهان يحاول إخباري بأن احتمالات الفوز بجائزة الـ 500 دولار هي 100 إلى 1. لا أتفق معه. أولًا، الصندوق الذي يحتوي على 0 + 7 لديه فرصة أفضل بكثير للفوز من الصندوق الذي يحتوي على 2 + 9. ومع ذلك، فإن احتمالات بقاء الرقمين الأخيرين 0 + 7 طوال اللعبة عالية. إذا تم اختيار الصناديق لك عشوائيًا، فهل يمكنك إخباري بالاحتمالات التقريبية للفوز بجائزة الـ 500 دولار؟
بافتراض اختيار خلايا الشبكة عشوائيًا، فإن احتمالات الفوز في أي ربع سنة ستكون ١/١٠٠. وبافتراض أن كل ربع سنة حدث مستقل، وهو ليس كذلك، فإن احتمالات الفوز في الأرباع الأربعة جميعها ستكون (١/١٠٠) ٤ = ١ من ١٠٠ مليون.
أود حقًا معرفة كيفية قراءة احتمالات مثل ١٢ إلى ١ أو ٣ إلى ٢. أيهما يُظهر أفضل فرص الفوز؟ ١٢ إلى ١ أم ٣ إلى ٢؟
لا أحبذ استخدام الاحتمالات بهذا الشكل، ولكنها تُستخدم عادةً بهذا الشكل: "احتمالات عدم الحصول على رويال فلش هي 649,739 إلى 1". هذا يعني أن هناك 649,739 احتمالًا لا يمكنك من خلالها الحصول على رويال فلش، وطريقة واحدة فقط يمكنك من خلالها. في أمثلتك، احتمال 12 إلى 1 هو 1/13، أو 7.69%، واحتمال 3 إلى 2 هو 2/5، أو 40.00%، لذا فإن احتمال 3 إلى 2 هو الأفضل للفوز.
في مقالٍ بصحيفة سانت لويس بوست ديسباتش، يقول المراسل: "فيضان كل 500 عام هو فيضانٌ احتمال حدوثه واحدٌ من أصل 500 في أي عام. وبعبارةٍ أخرى، احتمال حدوثه واحدٌ من أصل 10 على مدار 50 عامًا، أو واحدٌ من أصل 5 على مدار قرن." بعد قراءة جميع صفحاتكم المتعلقة بالمقامرة، أعتقد أن هذه ليست طريقةً صحيحةً للتعبير عن الأمر، أليس كذلك؟ بناءً على ادعاءاتهم، يعني هذا أن احتمال حدوث فيضان كل 500 عام هو واحدٌ من أصل 1، وهذا مستحيلٌ على الإطلاق.
أنت محق، هذه المقالة غير صحيحة. احتمال حدوث فيضان كل ٥٠٠ عام خلال فترة س سنوات هو ١-e -x/٥٠٠ . لذا، فإن احتمال حدوث فيضان واحد على الأقل كل ٥٠٠ عام خلال ٥٠ عامًا هو ٩.٥٢٪، وخلال ١٠٠ عام هو ١٨.١٣٪.
إذا حددتُ قيمة الرهان العادلة للعبة -160/+160، ووجدتُ خطًا غير صحيح -145، فما هي قيمة EV الخاصة بي؟ سأكون ممتنًا للغاية لأي صيغة يُمكنني من خلالها حساب قيمة EV الخاصة بي +/- بعد تحديد قيمة الرهان العادلة.
ليكن p هو احتمال فوز المرشح الأوفر حظًا. إذا كان -160 خطًا عادلًا، فإن:
100*ص - 160*(1-ص) = 0
260 بكسل = 160
ص = 160/260 = 8/13 = 61.54%.
لذا، العائد المتوقع لرهان بقيمة 145 دولارًا أمريكيًا عند خط -145 هو (8/13) × 100 + (5/13) × -145 = 75/13 = 5.77 دولارًا أمريكيًا. وبالتالي، ستكون ميزة اللاعب 5.77 دولارًا أمريكيًا / 145 دولارًا أمريكيًا = 3.98%.
لنُعرّف t بأنه خط المال الحقيقي بدون ميزة الكازينو، وa بأنه خط المال الفعلي. فيما يلي صيغ حساب العائد المتوقع للاعب:
أ سالب، ت سالب: (100*(ta) / (أ*(100-ت))
A موجب، t موجب: (at)/(100+t)
أ موجب، ت سالب: (أ*ت + 10000)/((ت-100)*100)
لذلك في حالتك، العائد المتوقع هو 100*(-160 -(-145))/(-145*(100-(-160))) = 3.98%.
ما رأيك في الادعاء أدناه، بأن الله ديمقراطي كما يتضح من حقيقة أن جميع المقاطعات التي صوتت لصالح جور في عام 2000 نجت من الأعاصير الثلاثة التي ضربت فلوريدا مؤخرًا؟
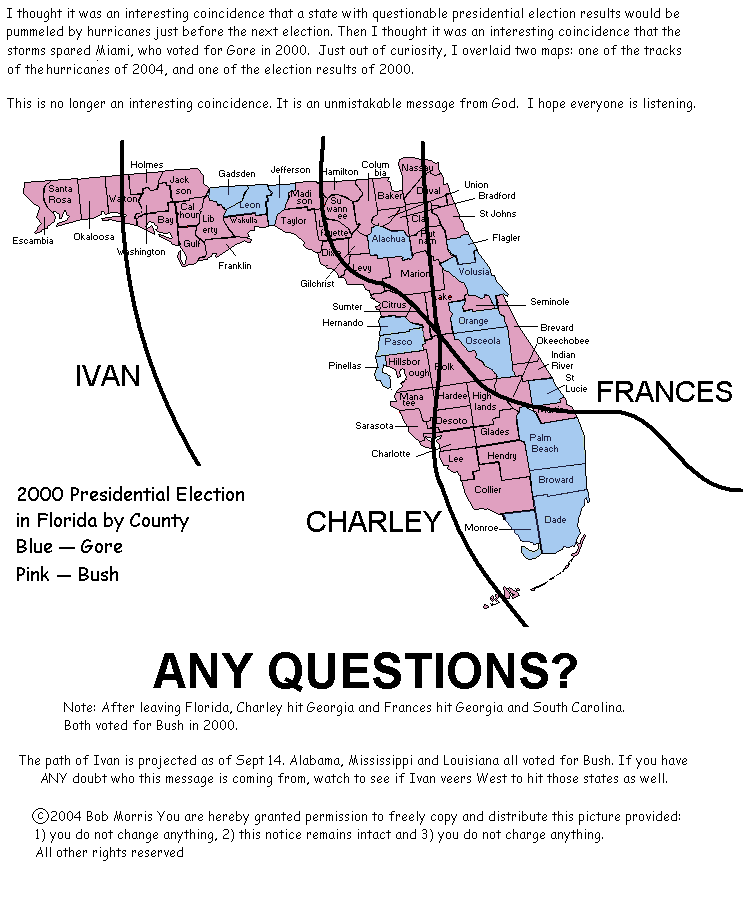
أولاً، أنشر هذا لأن المؤلف سمح بذلك في الأسفل. هذا مثال جيد على أن الارتباط لا يعني بالضرورة السببية. من السهل العودة بالزمن إلى الوراء والعثور على الكثير من المصادفات. لإثبات أي شيء، يجب طرح فرضية قبل جمع أي دليل.
متابعة (١٣ نوفمبر ٢٠٠٤): أشار قارئ آخر إلى أن هذه الخريطة كانت في البداية مزحة، ثم تحولت إلى أسطورة شعبية . وكما يشير هذا الرابط، فإن مسارات الأعاصير في الرسم البياني غير دقيقة، وأن الأعاصير ضربت العديد من مقاطعات غور. هذا يُظهر أنه لا يجب تصديق كل ما تقرأه، وخاصةً على الإنترنت.
فكرتُ فقط أن هذا قد يثير اهتمامك. يقدم موقع Bodog الرهان التالي: "هل سيكون طفل بريتني سبيرز وكيفن فيدرلاين الثاني صبيًا أم فتاة؟" احتمالات ولادة صبي هي +105، و-145 لفتاة. آخر مرة تحققتُ فيها من هذا، كانت النسبة 1:1 منذ بداية البشرية. أود أن أعرف من يراهن على احتمال -145 في هذا الرهان. أحب الموقع، وأزوره باستمرار، وأُعرب عن تقديري لرعايتك.
شكراً على كلماتك الطيبة. بصراحة، لم يعد أحد يهتم كثيراً بمعدلات النقر. لذا، لا تشعر بأنك مُلزم بالنقر على اللافتات إذا كان الأمر مجرد مظهر. للإجابة على سؤالك، في الولايات المتحدة، احتمالات فوز الذكور قريبة جداً من 50.5% وفوز الإناث 49.5%. بافتراض عدم وجود معلومات أخرى معروفة لدى مجتمع المراهنات، ستكون ميزة اللاعب في رهان الذكور 0.505 × 1.05 - 0.495 = 3.53%. قد يكون هناك شخص مطلع يراهن على أنثى. نظرية أخرى هي أن بعض الناس يعتقدون خطأً أنه يمكن تحديد جنس المولود من خلال شكل بطن الأم، وهؤلاء الأشخاص يراهنون على أنثى. شخصياً، سأترك هذا الأمر كما هو.
في هذا الفيديو على يوتيوب ، يقول مات ديمون إن احتمالية عدم نجاة جون ماكين من ولايته الأولى هي 1 من 3. هل هو محق؟
لا. باستخدام هذا الجدول الاكتواري من مراكز السيطرة على الأمراض والوقاية منها (CDC)، فإن احتمالية نجاة رجل أبيض يبلغ من العمر 72 عامًا حتى سن 76 هي 85.63%. أي ما يعادل احتمال وفاة واحد من سبعة. يمكن حساب معدل البقاء على قيد الحياة بقسمة عدد المواليد في سن 76، والبالغ 57,985، على عدد المواليد في سن 72، والبالغ 67,719، من جدول الذكور البيض في الصفحة 14. الجدول المستخدم يُسمى "جدول حياة الفترة"، ويفترض أن معدلات الوفيات لعام 2003 لن تتغير في المستقبل، وهو النوع الأكثر شيوعًا من الجداول الاكتوارية. قد يرغب شخص مثالي في استخدام جدول حياة عام 1936، لكنني لا أعتقد أنه سيُحدث فرقًا كبيرًا.
ملاحظة: بعد نشر هذه الإجابة، تلقيتُ عدة تعليقات تفيد بأن ردي لم يأخذ في الاعتبار الحالة الصحية لجون ماكين. كونه ناجيًا من السرطان يعمل ضده. أما حصوله على أفضل رعاية طبية ممكنة، فهو بلا شك يتمتع بصحة عقلية وجسدية جيدة لشخص في الثانية والسبعين من عمره، وطول عمره، كما يتضح من بقاء والدته على قيد الحياة. مع ذلك، لم أقصد أبدًا الأخذ بهذه المعلومات في الاعتبار. كان مات ديمون هو من استشهد بجداول اكتوارية، وهو ما كنت أشير إليه. كل ما أقوله هو أن احتمالية بقاء الرجل الأبيض العادي البالغ من العمر 72 عامًا على قيد الحياة لأربع سنوات أخرى هي 86%. ولو اضطررتُ لذلك، لتوقعتُ أن تكون احتمالات بقاء جون ماكين على قيد الحياة أفضل من ذلك.
مع كمية متساوية من الورق، أيٌّ من الأكواب الورقية سيتسع لكمية أكبر من الماء، أسطواني أم مخروطي؟ لنفترض أن الأسطوانة مفتوحة من أحد طرفيها، وأبعادها مثالية في كلا الحالتين.
يرجى الاطلاع على موقعي المرافق MathProblems.info ، المشكلة رقم 210، للحصول على الإجابة والحل.
هل سمعتم بقصة الأميرة، الجمل في حديقة حيوانات بوب كورن بارك في نيوجيرسي، التي حققت 88 فوزًا مقابل 51 خسارة في تقييم دوري كرة القدم الأمريكية؟ ما هي احتمالات ذلك؟
باستثناء الدفعات، فإن احتمالية تحقيق 88 فوزًا على الأقل من أصل 139 اختيارًا هي 0.00107355، أو 1 من 931. هذا مُخيّب للآمال. أنا متأكد من وجود 930 حيوانًا آخر أدوا أداءً أسوأ، لكن لا أحد يكتب عنهم. لمزيد من المعلومات عن برينسيس، اقرأ مقال " جمل نيوجيرسي يتنبأ بفوز العمالقة على الباتريوتس" على موقع ESPN.com.
في برنامج تشيلسي ليتلي، الذي عُرض في 8 مايو 2012، قالت تشيلسي إن أصحاب الشعر الأحمر ينقرضون لأنهم لا يتزاوجون. هل هذا صحيح؟
آمل أن تكون سعيدًا؛ لقد أمضيت ساعات في هذا.
للإجابة على هذا السؤال، من المهم قياس السلوك وفقًا لفرضية تشيلسي هاندلر ذات الشعر الأحمر. إليكم افتراضاتي.
- لن يتزاوج رأس أحمر أبدًا مع رأس أحمر آخر.
- الأنثى ستختار دائما الذكر للتزاوج معه.
- سوف يتزاوج الجميع، وكل تزاوج سوف ينتج نفس العدد من الأطفال.
- ستحصل الإناث ذات الشعر الأحمر على الأولوية في اختيار شريك حياتها، من خلال الاختيار بشكل عشوائي بين غير ذوات الشعر الأحمر.
- ستختار الإناث الحاملات للجين (والتي لديها جين الشعر الأحمر) شريكًا بشكل عشوائي من بين الرجال المتبقين من ذوات الشعر الأحمر.
- ستختار الإناث السلبية (لا تحمل أي جين الشعر الأحمر) بشكل عشوائي من بين الرجال المتبقين من ذوي الشعر الأحمر والحاملين.
أبدأ باحتمالية ٤٪ لأصحاب الشعر الأحمر، وفقًا لموقع Today I Found It . ثم أفترض أنه قبل ذلك لم يكن هناك أي تحيز ضد أصحاب الشعر الأحمر.
بافتراض أن التحيز ضد ذوي الشعر الأحمر يبدأ من الجيل التالي ويستمر، فما هو اتجاه إجمالي السكان نحو الشعر الأحمر؟ بعد عملٍ مُكثّف في جدول بيانات، لن أخوض فيه، إليكم الأجيال الثمانية الأولى، بدءًا من هذا الجيل.
نسبة الشعر الأحمر
| جيل | حَجم |
|---|---|
| 1 | 4.000000% |
| 2 | 3.888889% |
| 3 | 3.895219% |
| 4 | 3.894863% |
| 5 | 3.894883% |
| 6 | 3.894882% |
| 7 | 3.894882% |
| 8 | 3.894882% |
ما نراه هو أنه بحلول الجيل الثالث، ستقترب نسبة السكان ذوي الشعر الأحمر من 3.90%. لذا، بغض النظر عما قد تقوله تشيلسي، أعتقد أن أصحاب الشعر الأحمر لا داعي للقلق.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
وفقًا لموقع CardPlayer.com ، يبيع أمير ليهافوت، أحد اللاعبين التسعة الذين وصلوا إلى الطاولة النهائية في بطولة العالم للبوكر لعام ٢٠١٣، أي أرباح تزيد عن الحد الأدنى البالغ ٧٣٣,٢٢٤ دولارًا أمريكيًا للفوز بالمركز التاسع بسعر ٢٩,٢٤٨ دولارًا أمريكيًا لكل ١٪ من أسهمه. هل هذا سعر عادل؟
أولاً، دعونا نراجع مجموعات الرقائق.
مجموعات رقائق الطاولة النهائية لبطولة العالم للبوكر 2013
| لاعب | رقائق البطاطس |
|---|---|
| جيه سي تران | 38,000,000 |
| أمير لهفوت | 29,700,000 |
| مارك ماكلولين | 26,525,000 |
| جاي فاربر | 25,975,000 |
| ريان ريس | 25,875,000 |
| سيلفان لوسلي | 19,600,000 |
| ميشيل بروميلهويس | 11,275,000 |
| مارك نيوهاوس | 7,350,000 |
| ديفيد بينيفيلد | 6,375,000 |
يوضح الجدول التالي الفوز لكل نتيجة نهائية في البطولة.
جوائز مالية على الطاولة النهائية لبطولة العالم للبوكر 2013
| مكان | يفوز |
|---|---|
| الأول | 8,359,531 دولارًا |
| الثاني | 5,173,170 دولارًا |
| الثالث | 3,727,023 دولارًا |
| الرابع | 2,791,983 دولارًا |
| الخامس | 2,106,526 دولارًا |
| السادس | 1,600,792 دولارًا |
| السابع | 1,225,224 دولارًا |
| الثامن | 944,593 دولارًا |
| التاسع | 733,224 دولارًا |
بافتراض تساوي مهارات جميع اللاعبين، يُمكن تقدير احتمال الفوز بنسبة إجمالي رصيد الرقائق. ومع ذلك، يزداد الأمر تعقيدًا في كل مركز بعد ذلك. للمساعدة في الإجابة على هذا السؤال، طوّرتُ حاسبة بطولات البوكر الخاصة بي.
بعد إدخال المعلومات أعلاه، ستجد أن أمير يتوقع فوزًا قدره 3,658,046 دولارًا أمريكيًا. بعد طرح الحد الأدنى للجائزة، وهو 733,224 دولارًا أمريكيًا، للمركز التاسع، ستحصل على 2,924,822 دولارًا أمريكيًا من الأرباح غير المضمونة المتوقعة. تبلغ قيمة كل حصة 1% 29,248.22 دولارًا أمريكيًا. وهذا هو السعر المذكور في مقالة cardplayer.com.
بالمناسبة، حلّ فريق ليهافوت ثالثًا، وحصل على جائزة مالية قدرها 3,727,023 دولارًا. بطرح مبلغ 733,224 دولارًا المضمون للمركز التاسع وقسمة الناتج على 100، ربح كل سهم بنسبة 1% 29,938 دولارًا. كانت التكلفة الأصلية للسهم 29,248 دولارًا، أي أن كل سهم كان سيحقق ربحًا بنسبة 2.36%.
تمت مناقشة هذا السؤال في منتدياتي في Wizard of Vegas .
بالنسبة لعروض الكازينو التي لا تزال تستخدم التذاكر العادية في أسطوانة حقيقية (وليس الإلكترونية)، حيث تطبع تذاكرك على مكتب اللاعبين وتضعها في الأسطوانة، هل تثني/تطوي تذاكرك قبل وضعها في الأسطوانة؟ هل تعتقد أن التذاكر المنحنية لديها فرصة أفضل للفوز؟
أتمنى أن تكون سعيدًا. للإجابة على هذا السؤال، اشتريتُ لفافة تذاكر كبيرة من متجر أوفيس ديبوت. ثم وضعتُ 500 تذكرة في كيس ورقي، نصفها مطوي إلى نصفين بزاوية 90 درجة تقريبًا، والنصف الآخر مفتوح. ثم طلبتُ من ستة متطوعين سحب ما بين 40 و60 تذكرة واحدة تلو الأخرى، مع استبدالها، بينما كنتُ أسجل النتائج. إليكم النتائج.
تجربة رسم التذكرة
| موضوع | مطوية | مكشوفة | المجموع |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| المجموع | 175 | 125 | 300 |
وبالتالي، تم طي 58.3% من التذاكر المسحوبة!
إذا افترضنا أن طيّ البطاقات لم يكن له تأثير، فإن هذه النتائج ستكون بعيدة عن التوقعات بمقدار 2.89 انحراف معياري. احتمال الحصول على هذا العدد من البطاقات المطوية، أو أكثر، بافتراض أن طيّ البطاقات لم يؤثر على احتمالات الفوز، هو 0.19%، أو 1 من 514.
أود أن أضيف أن المشاركين الذين سحبوا التذاكر على عجل كانوا أكثر عرضة لسحب بطاقات مطوية. أما أولئك الذين حرصوا على وقتهم في كل سحب، فكانت نسبة فوزهم متساوية تقريبًا.
لذا، استنتاجي هو بالتأكيد أن أطويهم.
لمناقشة هذا السؤال، يرجى زيارة منتدياتي في Wizard of Vegas .
يُوزّع رقم عشوائي لكلٍّ من لاعبين في (0،1). يقرر اللاعب الأول إما البقاء على حاله أو التخلص من الورقة وسحب رقم جديد. يفعل اللاعب الثاني الشيء نفسه. يفوز صاحب الرقم الأعلى. ما هي الاستراتيجية الأمثل لكل لاعب؟ بافتراض الاستراتيجية الأمثل، ما هو احتمال فوز كل لاعب؟
لنفترض أنك عُرضت عليك فرصة لعب لعبة رمي العملة. إذا كانت النتيجة في الرمية الأولى صورة، فستسترد دولارين وتنتهي اللعبة. وإلا، فستُعيد رمي العملة. إذا كانت النتيجة في الرمية الثانية صورة، فستسترد 4 دولارات. إذا كانت النتيجة في الرمية الثانية أيضًا صورة، فستستمر في رمي العملة حتى تحصل على صورة. في كل رمية، تتضاعف الجائزة. بمعنى آخر، ستسترد 2^n، حيث n هو عدد مرات الرمي (بما في ذلك الرمية الأخيرة التي كانت النتيجة فيها صورة). كم ستدفع للعب هذه اللعبة؟ سمعت أن الإجابة الرياضية هي مبلغ لا نهائي من المال، لكن هذا غير منطقي، لأنه يجب أن تربح مبلغًا محدودًا من المال في مرحلة ما.
وهذا ما يُعرف باسم مفارقة سانت بطرسبرغ .
صحيحٌ أن الفوز المتوقع في اللعبة هو ∞، وفي الوقت نفسه، احتمالية سقوط العملة المعدنية على وجه الكتابة هي نفسها، مما يؤدي إلى مبلغ محدود من المال. حساب الفوز المتوقع هو:
الفوز المتوقع = pr(رمية واحدة) × 2 + pr(رميتان) × 4 + pr(3 رميات) × 8 + pr(4 رميات) × 16 + pr(5 رميات) × 32 + pr(6 رميات) × 64 + ... =
(1/2) 1 × 2 1 + (1/2) 2 × 2 2 + (1/2) 3 × 2 3 + (1/2) 4 × 2 4 + (1/2) 5 × 2 5 + (1/2) 6 × 2 6 + ...
= ((1/2)*(2/1)) 1 + ((1/2)*(2/1)) 2 + ((1/2)*(2/1)) 3 + ((1/2)*(2/1)) 4 + ((1/2)*(2/1)) 5 + ((1/2)*(2/1)) 6 + ...
= 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + ...
= 1 + 1 + 1 + 1 + 1 + 1 + ... = ∞
تكمن المفارقة في أن اللاعب يجب أن يربح مبلغًا محدودًا من المال، بينما الربح المتوقع لا نهائي. كيف يُعقل ذلك؟
ربما لا تكون هذه إجابة مُرضية، ولكن هناك الكثير من المفارقات فيما يتعلق بـ ∞. قد يُسبب لي هذا بعض الرسائل الإلكترونية الغاضبة، ولكن ما يُريحني، رغم هذه المفارقات اللانهائية، هو اعتقادي بأن ∞ مفهوم رياضي أو فلسفي لم يُثبت وجوده في الكون المادي الحقيقي. يحمل هذا المفهوم أو نظرية اللانهاية معه مفارقات مُضمنة.
لمن لا يتفق مع هذا الرأي، أرجو أن تخبروني بأي شيء ثبت أن له كمية أو قياسًا لا نهائيين. لا تقولوا إن للثقب الأسود كثافة لا نهائية إلا إذا كان لديكم دليل على حجمه.
للإجابة على السؤال الأولي حول المبلغ الذي يجب على المرء دفعه للعب هذه اللعبة، يجب أن نضع في اعتبارنا أن السعادة لا تتناسب مع كمية المال. شخصيًا، تعلمت في دروس الاقتصاد، وأعتقد أن المنفعة، أو السعادة، من المال تتناسب مع لوغاريتم كمية المال. بموجب هذا الافتراض، إذا قمت بزيادة أو نقصان ثروة أي شخصين بنفس النسبة المئوية، بخلاف الثروة الأولية التي تساوي صفرًا، فإن كلاهما يشهد نفس التغيير في السعادة. على سبيل المثال، إذا زادت ثروة جيم فجأة من 1000 دولار إلى 1100 دولار وزادت ثروة جون فجأة من 10000000 دولار إلى 11000000 دولار، فإن كلاهما يشهد نفس الزيادة في السعادة، لأنه في كلتا الحالتين زادت ثروتهما بنسبة 10٪. بافتراض أن السعادة من المال تتناسب بالفعل مع لوغاريتم المبلغ، فإن الجدول التالي يوضح أقصى مبلغ يجب أن يكون الشخص على استعداد لدفعه وفقًا لثروته قبل الدفع للعب.
اللامبالاة هي مقدار اللعب
| ثروة | اللامبالاة كمية |
|---|---|
| 10 دولارات | 4.97 دولارًا |
| 100 دولار | 7.79 دولارًا |
| 1000 دولار | 10.96 دولارًا |
| 10,000 دولار | 14.26 دولارًا |
| 100,000 دولار | 17.78 دولارًا |
| مليون دولار | 20.88 دولارًا |
| 10,000,000 دولار | 24.19 دولارًا |
| 100,000,000 دولار | 27.51 دولارًا |
| 1,000,000,000 دولار | 30.84 دولارًا |
كما ترى، في ظل ظروف واقعية، المبلغ الذي يجب دفعه أقل بكثير من ∞ دولار. على سبيل المثال، إذا كانت ثروتك مليون دولار، فلا داعي للمراهنة بمبلغ 20.88 دولارًا.
تم طرح هذا السؤال ومناقشته في منتدى Wizard of Vegas .
تحتوي يانصيب ميشيغان على لعبة ثلاثية اللاعبين وفقًا للقواعد التالية: هل هناك أي ميزة موقعية للتواجد في المركز الأخير في هذه اللعبة؟ ما هي الاستراتيجية الأمثل لكل لاعب؟ إليكم فيديوعلى يوتيوب يعرض اللعبة.
أولًا، لا توجد ميزة موقعية للتصرف الأخير. بما أن اللاعبين يُحفظون في حجرة عازلة للصوت أثناء لعب أي لاعب سابق، فلا يُهم الترتيب.
ثانيًا، يجب أن يكون هناك توازن ناش في اللعبة، حيث تكون استراتيجية البقاء برصيد x نقطة على الأقل أفضل من أي استراتيجية أخرى. السؤال هو إيجاد x.
ما فعلته هو أنني سألت نفسي: ما هي الاستراتيجية المتبعة إذا حصل كل لاعب، بدلاً من بطاقة مرقمة من ١ إلى ١٠٠، على رقم عشوائي موزع بالتساوي بين ٠ و١، وبحث عن النقطة س التي لا يكترث فيها أي منطقي مثالي بين التوقف والتبديل. بهذه الإجابة، يسهل تطبيقها على توزيع منفصل من ١ إلى ١٠٠.
سأتوقف عن الحديث هنا، وأترك لقرائي الاستمتاع بالمشكلة. للاطلاع على الإجابة والحل، يُرجى زيارة الروابط أدناه.
الإجابة على التوزيع المستمر من 0 إلى 1 .
الإجابة على التوزيع المنفصل من 1 إلى 100.
للحصول على حلي، الرجاء الضغط هنا (PDF) .
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لنفترض أن لديك مجموعة من عشر بطاقات حمراء وعشر بطاقات سوداء. بعد خلط عشوائي، سحبت بطاقات دون استبدال. ما احتمال سحب جميع البطاقات السوداء العشر قبل خمس بطاقات حمراء؟
هذا يشبه السؤال عن احتمال احتواء ١٤ بطاقة عشوائية على جميع البطاقات العشر السوداء. هناك مجموع (١٠، ٤) = ٢١٠ طريقة لاختيار ٤ بطاقات حمراء من أصل ١٠ في المجموعة. بالطبع، هناك طريقة واحدة فقط لاختيار جميع البطاقات العشر السوداء. هناك مجموع (٢٠، ١٤) = ٣٨٧٦٠ طريقة لاختيار ١٤ بطاقة من أصل ٢٠. إذن، الإجابة هي ٢١٠/٣٨٧٦٠ = ٠.٠٠٥٤١٨، أو ١ من ١٨٤.٥٧.
أعرف ترقية تُمنح مكافأة عند تحقيق أربعة أوراق متشابهة في جميع الرتب الـ ١٣. كم يدًا يتطلب هذا في المتوسط؟
دعونا نلقي نظرة على المعيار الذهبي لفيديو بوكر، 9-6 Jacks or Better للإجابة على سؤالك.
الخطوة الأولى هي تعديل آلتي الحاسبة لتشمل بندًا سطريًا لجميع الأنواع الأربعة الثلاثة عشر. هذا هو جدول الإرجاع المُعدَّل:
جدول إرجاع "جاك" المعدل أو "أفضل"
| حدث | يدفع | التركيبات | احتمال | يعود |
|---|---|---|---|---|
| دافق ملكي | 800 | 493,512,264 | 0.000025 | 0.019807 |
| فلاش مستقيم | 50 | 2,178,883,296 | 0.000109 | 0.005465 |
| أربعة أ | 25 | 3,900,253,596 | 0.000196 | 0.004892 |
| أربعة ك | 25 | 3,904,533,816 | 0.000196 | 0.004897 |
| أربعة أسئلة | 25 | 3,898,370,196 | 0.000196 | 0.004889 |
| أربعة ج | 25 | 3,886,872,684 | 0.000195 | 0.004875 |
| أربعة 10 | 25 | 3,471,687,732 | 0.000174 | 0.004354 |
| أربعة 9 | 25 | 3,503,226,684 | 0.000176 | 0.004394 |
| أربعة 8 | 25 | 3,504,128,652 | 0.000176 | 0.004395 |
| أربعة 7 | 25 | 3,504,825,252 | 0.000176 | 0.004396 |
| أربعة 6 | 25 | 3,504,861,888 | 0.000176 | 0.004396 |
| أربعة 5 | 25 | 3,504,895,944 | 0.000176 | 0.004396 |
| أربعة 4 | 25 | 3,504,032,676 | 0.000176 | 0.004395 |
| أربعة 3 | 25 | 3,503,177,148 | 0.000176 | 0.004394 |
| أربعة 2 | 25 | 3,502,301,496 | 0.000176 | 0.004393 |
| منزل كامل | 9 | 229,475,482,596 | 0.011512 | 0.103610 |
| تدفق | 6 | 219,554,786,160 | 0.011015 | 0.066087 |
| مستقيم | 4 | 223,837,565,784 | 0.011229 | 0.044917 |
| ثلاثة من نفس النوع | 3 | 1,484,003,070,324 | 0.074449 | 0.223346 |
| زوجان | 2 | 2,576,946,164,148 | 0.129279 | 0.258558 |
| جاكس أو أفضل | 1 | 4,277,372,890,968 | 0.214585 | 0.214585 |
| لا شئ | 0 | 10,872,274,993,896 | 0.545435 | 0.000000 |
| المجموع | 19,933,230,517,200 | 1.000000 | 0.995439 |
احتمال الحصول على أي أربعة من نفس النوع هو 0.002363.
السؤال التالي الذي يجب الإجابة عليه هو: كم عدد المجموعات الرباعية المتشابهة المطلوبة في المتوسط للحصول على جميع الأنواع الثلاثة عشر؟ للإجابة على هذا السؤال، أنشأتُ حاسبة التجارب المتوقعة . لاستخدامها، أدخل عدد مجموعات كل مجموعة رباعية متشابهة في أول ثلاثة عشر خانة. ستخبرك الحاسبة أن العدد المتوقع من المجموعات الرباعية المتشابهة هو 41.532646 للحصول على جميع الأنواع الثلاثة عشر.
وبالتالي، فإن العدد المتوقع للأيدي التي يتم لعبها للحصول على 13 بطاقة من نوع واحد هو 41.341739/0.002363 = 17,580.
يمكن لحقل العشب أن يغذي بالضبط:
بقرة واحدة ولاما واحدة لمدة 21 يومًا.
لاما واحدة وخروف واحد لمدة 42 يومًا.
خروف واحد وبقرة واحدة لمدة 28 يومًا.
تأكل البقرة من العشب بقدر ما تأكله اللاما والأغنام معًا.
ينمو العشب بمعدل ثابت.
كم من الوقت سوف يستغرق الحيوانات الثلاثة معًا لالتهام حقل العشب بالكامل؟
[حرق] دع:
ج = معدل أكل البقرة للعشب
l = معدل أكل اللاما للعشب
س = معدل أكل الخروف للعشب
g = معدل نمو العشب
في نهاية فترة زمنية محددة، يجب أن يساوي العشب المستهلك الكمية الأولية منه مضافًا إليها كمية العشب المزروع خلال تلك الفترة. لذا...
(1) 21*(ج+ل) = 1 + 21ج
(2) 42*(l+s) = 1+42g
(3) 28*(س+ج) = 1+28ج
حيث يمثل الرقم 1 حقلًا واحدًا من العشب.
وقد أعطينا أيضا:
(4) ج=س+ل
أولاً، استبدل المعادلة (4) في (2):
(5) 42 ج = 1 + 42 ج
عبر عن ذلك من حيث g:
(6) ج = (42ج-1)/42
بعد ذلك، استبدل المعادلة (6) في (1)...
(7) 21(ج+ل) = 1 + 21*(42ج-1)/42
بعد القليل من الجبر نحصل على ...
(8) ل = 1/42.
بعد ذلك، استبدل المعادلة (4) في (3)...
(9) 28*(2س + ل) = 1+28ج
نحن نعلم أن l=1/42، لذا...
28*(2س + 1/42) = 1+28ج
56 ثانية + 28/42 = 1 + 28 جرام
2352 ثانية + 28 = 42 + 1176 جرام
(10) ج = (2352 ثانية - 14)/1176
بعد ذلك، استبدل المعادلتين (8) و (10) في (2) ...
42*(1/42 + ثانية) = 1 + 42*(2352 ثانية - 14)/1176
بعد بعض الجبر السهل نحصل على:
(11) س = 14/1176 = 1/84
من المعادلة (4)
(12) ج = (1/84) + (1/42) = 3/84 = 1/28
لذا، إذا لم ينمو العشب، فسوف يستغرق البقر 28 يومًا لتناول العشب في الحقل، واللاما 42 يومًا، والأغنام 84 يومًا.
الآن، لنحل المعادلة g. نستبدل (11) في (10):
g = [2352*(1/84)- 14]/1176
(13) ج = 14/1176 = 1/84.
ومن قبيل الصدفة، فإن هذه هي نفس السرعة التي تأكل بها الأغنام العشب.
لتكن الإجابة النهائية هي t. نعلم أن كمية العشب المأكولة خلال t أيام يجب أن تساوي كمية العشب في الحقل (1) زائد العشب المزروع خلال تلك الفترة. إذًا...
(13) t*(s+l+c) = 1 + tg
حل ل...
t*[(1/84) + (1/42) + (1/28)] = 1 + t/84
t = 1/[(1/84) + (1/42) + (1/28) - (1/84)]
(14) t = 84/5 = 16.8 يومًا = 16 يومًا و19 ساعة و12 دقيقة
[/spoiler]
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas.
ما هو متوسط المسافة بين نقطتين عشوائيتين في مربع الوحدة؟
بالنسبة لسؤال سهل الطرح، فإن الحل معقد بعض الشيء. بالطريقة التي اتبعتها، ستحتاج إلى معرفة هذا التكامل .
وهنا الجواب والحلي (PDF) .
ما هي مسألة الرياضيات الموجودة على السبورة في فيلم Good Will Hunting ؟
كان الأمر سهلاً للغاية، خاصةً بالنسبة لدورة في الرياضيات التوافقية في معهد ماساتشوستس للتكنولوجيا. إليكم صياغة المسألة:
"ارسم جميع الأشجار غير القابلة للاختزال بشكل متجانس بحجم n=10."
وهنا محاولتي لتوضيح الأمر بلغة واضحة وبسيطة.
باستخدام خطوط مستقيمة فقط، ارسم جميع الأشكال التي يكون مجموع تقاطعاتها ونهاياتها المسدودة ١٠. لا يُسمح بوجود أي حلقات مغلقة، ولا يُسمح بوجود شكلين متكافئين. يجب أن يكون لأي تقاطع ثلاثة مسارات على الأقل تؤدي منه.
قد تتساءل، ماذا أقصد بـ "المكافئ"؟ يعني أنه يمكنك تحريك القطع، مع ترك التقاطعات كما هي، بأي طريقة تريدها، ولن ينتج عن ذلك أي أشكال جديدة.
وهنا مثال: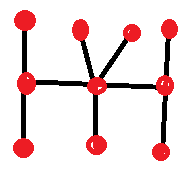
سأعطيك تلميحًا. على عكس الإجابة في الفيلم، هناك عشرة منها. ويل لديه ثمانية منها فقط. حاول أن تُضاهي ويل هانتينغ أو تهزمه.
[كابح]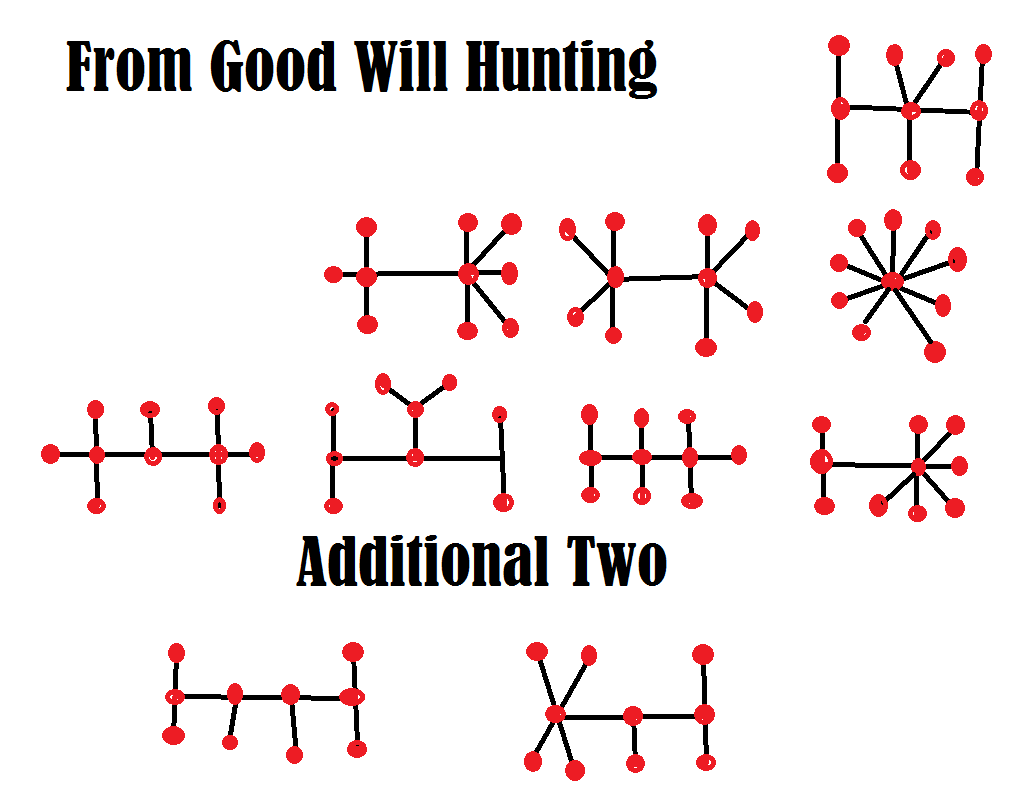
أظهر منطقي في التوصل إلى جميع العشرة في موقعي MathProblems.info ، المشكلة رقم 220.
[/spoiler]قراءة إضافية:- الرياضيات في صيد حسن النية 2: مشاكل من وجهة نظر الطلاب - ورقة أكاديمية حول المشكلة.
- مسألة الرياضيات الخاصة بصيد النوايا الحسنة -- مناقشة حول هذه المسألة في المنتدى الخاص بي.
فكر في لعبة بالقواعد التالية:
- يوفر مولد الأرقام العشوائية أرقامًا عشوائية بين 0 و1 موزعة بشكل موحد.
- يحصل كل لاعب على رقم منفصل. يستطيع كل لاعب رؤية رقمه الخاص فقط.
- يمكن للاعب 1 الاحتفاظ برقمه الأولي أو تبديله برقم عشوائي جديد.
- اللاعب 2، الذي يعرف تصرف اللاعب 1، لديه نفس الخيار للاحتفاظ برقمه الأصلي أو تبديله برقم جديد.
- يفوز اللاعب الذي لديه الرقم الأعلى.
لدي أربعة أسئلة حول اللعبة:
- أجب عن الأسئلة التالية حول اللعبة:
- عند أي رقم يصبح اللاعب 1 غير مبالٍ بالوقوف والتبديل؟
- بافتراض أن اللاعب 1 يقوم بالتبديل، عند أي رقم يجب أن يكون اللاعب 2 غير مبالٍ بالوقوف والتبديل؟
- بافتراض أن اللاعب 1 يقف، عند أي رقم يجب أن يكون اللاعب 2 غير مبالٍ بالوقوف والتبديل؟
- بافتراض الاستراتيجية المثلى لكلا اللاعبين، ما هو احتمال فوز اللاعب 1؟
يمكنك العثور على الإجابة والحل في صفحتي الخاصة بمشاكل الرياضيات ، المشكلة رقم 225.
سأشارك في مسابقة "الميت بول" لعام ٢٠١٨. إليكم القواعد:
- يجب على كل لاعب تقديم قائمة تتضمن عشرة مشاهير أحياء تقل أعمارهم عن 100 عام.
- إذا مات أي من المشاهير، كما أشارت وكالة أسوشيتد برس في عام 2018، فإن أي شخص يحمل اسم المشاهير في قائمته سيحصل على 100 نقطة، حيث x هو العمر عند الوفاة.
- يفوز اللاعب الذي لديه أكبر عدد من النقاط في 1/1/2019.
انطلاقا من المتوسطات، ما هي الاستراتيجية المثلى لهذه اللعبة؟
بصفتك خبيرًا إكتواريًا سابقًا، فقد سألتَ الشخص المناسب. آمل ألا تعتبر جمعية الخبراء الإكتواريين إجابتي إساءةً للمهنة. مع ذلك، وللإجابة على سؤالك، استشرتُ جدول عمر الفترة لعام ٢٠١٤ من مكان عملي السابق، مكتب كبير الخبراء الإكتواريين في إدارة الضمان الاجتماعي.
يوضح جدول حياة الفترة، من بين أمور أخرى، احتمال الوفاة لشخص في أي عمر وجنس معينين في عام 2014. وباستخدام هذه المعلومات، قمت بإنشاء الجدول التالي، الذي يوضح احتمال الوفاة والنقاط المتوقعة لجميع الأعمار من 0 إلى 100 وكلا الجنسين.
جدول الحياة للفترة 2014 - مجموعة الوفيات
| عمر | احتمالية الموت - ذكر | احتمالية الموت - أنثى | مُتوقع النقاط — ذكر | مُتوقع النقاط — أنثى |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 13 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 25 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 26 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 27 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 28 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 29 | 0.001454 | 0.000648 | 0.103234 | 0.046036 |
| 30 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 32 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 34 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 35 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 36 | 0.001781 | 0.001008 | 0.113970 | 0.064538 |
| 37 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 38 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 39 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 42 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 44 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 47 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 48 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
يوضح الجدول أن الحد الأقصى للنقاط المتوقعة لرجل يبلغ من العمر 90 عامًا هو 1.645220.
تم طرح هذا السؤال ومناقشته في منتدياتي غير المخصصة للمقامرة، Diversity Tomorrow .
إذا كنت تريد احتواء 355 مليلترًا في علبة، ما هي الأبعاد التي يجب أن تكون عليها لتقليل مساحة السطح؟
سؤال جيد! كنتُ أتساءل عن هذا عندما رأيتُ علب صودا رفيعة في معرض ألعاب، بسعة ٣٥٥ مليلترًا، وهو الحجم المعتاد. من المؤكد أن كلا الاسمين غير صحيح (ولا تناديني شيرلي). [حرق للأحداث] دعوني:
r = نصف قطر العلبة
h = ارتفاع العلبة
v = حجم العلبة
س = مساحة سطح العلبة
نعلم من الهندسة البسيطة أن مساحة السطح = 2*pi*r^2 + 2*pi*r*h.
وبنفس الطريقة، نعلم أيضًا أن الحجم هو pi*r^2*h، والذي أعطيناه يساوي 355.
لذا، 355=pi*r^2*h.
دعونا نعيد ترتيب ذلك إلى:
(1) ح = 355/(باي*ر^2)
نحن نعلم:
(2) س = 2*باي*ر^2 + 2*باي*ر*ح.
لنحصل على ذلك لدالة متغير واحد فقط عن طريق استبدال تعبيرنا عن h في المعادلة (1) في (2):
s = 2*pi*r^2 + + 2*pi*r*(355/(pi*r^2))) = 2*pi*r^2 + 710/r.
دعونا نأخذ المشتقة لـ s ونجعلها مساوية للصفر، لحل r الأمثل.
ds/dr = 4*pi*r - 710/(r^2 ) = 0
4*pi*r = 710/(r^2)
ضرب كلا الطرفين بـ r^2:
4*pi*r^3 = 710
r^3 = 177.5/باي.
ص = (177.5/بي) ^ (1/3) = 3.837215248.
أدخل هذه القيمة في المعادلة (1) للحصول على h = 7.674430496.[/spoiler]
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يبدو لي أن معظم محترفي المقامرة الذين أعرفهم يُفضلون معرفة تقلب اللعبة مُعبرًا عنه بالتباين بدلًا من الانحراف المعياري. بالطبع، الأول هو مجرد مربع الثاني. مع ذلك، أُفضل الانحراف المعياري لأنه بنفس وحدات الرهان والربح/الخسارة. ربما يُفضلون رقمًا أكبر لإبراز تقلب أكبر؟ ما رأيك - هل يُفضل المقامرون استخدام "التباين"، وإذا كان الأمر كذلك، فلماذا؟
أوافقك الرأي بأنك تسمع تباين اللعبة أكثر من انحرافها المعياري، وهو أمرٌ لطالما وجدته مزعجًا بعض الشيء. أعتقد أن السبب الذي يدفع المقامرين للاهتمام بتقلب اللعبة هو ربط الفوز أو الخسارة باحتمالية جلسة لعب. على سبيل المثال، ما هي نسبة الخسارة الفادحة 1% بعد 200 جولة بلاك جاك؟ للإجابة على ذلك، يمكنك استخدام الانحراف المعياري للبلاك جاك، وهو حوالي 1.15، حسب القواعد.
الإجابة المحددة لهذا السؤال هي 1.15 × 200^0.5 × -2.32635 (وهي نقطة 1% على المنحنى الغاوسي) = -37.83 وحدة أقل من المتوقع. تذكر أنه نظرًا لنسبة ربح الكازينو، يمكنك توقع خسارة. إذا افترضنا أن نسبة ربح الكازينو 0.3%، فبعد 200 يد، يمكنك توقع خسارة 0.003 × 200 = 0.6 يد. لذا، فإن خسارة 1% ستكون 0.6 + 37.83 = 38.43 يد.
سمعتُ أن احتمالية انتهاء الزواج بالطلاق، والتي تُقدّر عادةً بنسبة ٥٠٪ في الولايات المتحدة، تُحسب بقسمة عدد حالات الطلاق على عدد الزيجات في نفس الفترة الزمنية. هل هذا صحيح؟ هل تعتقد أن هذه طريقة عادلة لحساب هذه الإحصائية؟ أشك في ذلك لأنك تنظر إلى حالات الطلاق خلال فترة قصيرة مقارنةً بالزيجات التي استمرت لفترة طويلة.
إذا كان توزيع السكان والعمر مستقراً، وإذا كانت احتمالية الطلاق 50% حقاً، فإننا نتوقع أن نرى نسبة طلاق واحد إلى زواجين في أي فترة زمنية معينة، نظراً لحجم العينة الكبير.
مع ذلك، فإن عدد السكان ليس مستقرًا. من هذا الرسم البياني، يبدو أن عدد سكان الولايات المتحدة ينمو بنسبة 10.71% كل عقد، أي ما يعادل 1.02% سنويًا. لنفترض 1% فقط لتبسيط الأمر.
مصدر الخريطة: تعداد الولايات المتحدة
وفقًا لموقع fatherly.com ، يبلغ متوسط مدة الزواج غير الناجح 8 سنوات.
إذا كنت تلاحظ نسبة 1 إلى 2 من حالات الطلاق إلى الزواج في الوقت الحاضر، ما هو متوسط احتمال انتهاء أي زواج معين بالطلاق؟
حالات الطلاق التي نشهدها الآن كانت من زيجات قبل ثماني سنوات، عندما كانت نسبة السكان 92.35% مما هي عليه الآن. تشير عملية حسابية بسيطة إلى أن الاحتمال الحقيقي للطلاق هو 54.14%.
دعونا نتحقق من ذلك.
أولاً، وفقًا لمراكز السيطرة على الأمراض والوقاية منها، يبلغ معدل الزواج 6.9 لكل 1000 حالة زواج سنويًا. هذا الرقم لا علاقة له بالسؤال المطروح، ولكنه يساعد على فهم الأرقام المعنية.
لنفترض أن عدد السكان قبل ثماني سنوات كان 300 مليون نسمة. هذا يعني 0.69% × 300 مليون = 2,070,000 حالة زواج في تلك السنة.
إذا انتهى 54.14% منهم بالطلاق بعد ثماني سنوات، فإننا سنرى 2,070,000 * 54.14% = 1,120,698 حالة طلاق في الوقت الحاضر.
1,120,698 / 2,070,000 = 50% نسبة حالات الطلاق إلى حالات الزواج في الوقت الحاضر.
حتى لا يجادل أحد، نعم، أعلم أن حالات الطلاق لا تنتهي جميعها خلال ثماني سنوات بالضبط. ومع ذلك، بالنظر إلى كل شيء، أقول إن النتيجة النهائية لن تكون بعيدة عن نسبة الطلاق الحقيقية التي أتوقعها، وهي 54.14%.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يُجري مكتبك، الذي يضم مئة موظف، تبادل هدايا "بابا نويل السري". في هذه المسابقة، تكتب أسماء كل شخص على أوراق منفصلة، وتضعها في قبعة، ثم يسحب كل شخص اسمًا عشوائيًا ليقدم له هدية.
السؤال هو: كم عدد الحلقات المغلقة في المتوسط؟ على سبيل المثال، في حلقة مغلقة، يُعطي جوردون لدون، الذي يُعطي لجون، الذي يُعطي لناثان، الذي يُعطي لجوردون. أو سحب اسمك.
تخيل أن كل شخص يختار واحدًا تلو الآخر. عند اختيار كل شخص، سيكون هناك نوعان من المواقف:
- لقد تم اختيار اسم الشخص الذي يقوم بالقطف بالفعل.
- اسم الشخص الذي يقوم بالتقاط الصورة لا يزال موجودًا في سلة الأسماء.
بالنسبة لأي أداة اختيار معينة، لنفترض أن هناك n شخصًا متبقيًا للاختيار.
إذا كان اسم الشخص الذي يختار قد تم اختياره بالفعل، فهناك احتمال 1/n أن يختار إغلاق حلقة تتضمن اسمه. على سبيل المثال، لنفترض أن آمي تختار. اسم آمي موجود بالفعل لدى بوب، واسم بوب موجود بالفعل لدى تشارلي، واسم تشارلي لا يزال في سلة المهملات. بوجود n اسم لا يزال في سلة المهملات، هناك احتمال 1/n أن تختار آمي اسم تشارلي، مما يُغلق حلقة.
إذا لم يتم اختيار اسم الشخص الذي يقوم بالتقاط الصورة بالفعل، فهناك فرصة 1/n لأن تختار إيمي اسمها، مما يؤدي إلى إغلاق الحلقة.
على أي حال، إذا لم تُغلق المُلتقطة حلقة، فهي تُشارك في جزء من سلسلة أخرى، والتي سيُغلقها شخص آخر في النهاية. يجب احتساب كل سلسلة مرة واحدة فقط عند إغلاقها.
وبالتالي فإن الإجابة هي 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518.
التقدير لأي عدد كبير بما فيه الكفاية من اللاعبين، n، هو ln(n).
تم طرح السؤال ومناقشته في المنتدى الخاص بي في Wizard of Vegas .
تكريمًا لعمود اسأل المعالج رقم 314، ما هي السلاسل اللانهائية المفضلة لديك التي يصل مجموعها إلى وظيفة من وظائف باي؟
من السهل اختيار هذين الاثنين، لأنهما على الأرجح الأكثر شهرة:
- 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
- 1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 + ... = π^2/6
سمعتُ أنه مع ٢٣ شخصًا عشوائيًا، فإن احتمالية وجود عيد ميلاد مشترك واحد على الأقل لشخصين أو أكثر تزيد عن ٥٠٪. هل هذا صحيح؟ ما هو احتمال وجود عيد ميلاد مشترك لمجموعات أخرى بأحجام مختلفة؟ نفس السؤال ينطبق أيضًا على عيد ميلاد مشترك لثلاثة وأربعة وخمسة أشخاص.
هذا صحيح، فمع وجود ٢٣ شخصًا عشوائيًا، فإن احتمالية وجود تاريخ ميلاد مشترك لزوجين على الأقل هي ٥٠٫٧٣٪. هذا يتجاهل اليوم الكبيس، ويفترض أن لكل شخص فرصة متساوية للولادة في كل يوم من الأيام الـ ٣٦٥ الأخرى (وهو ليس صحيحًا، فأعياد الميلاد في الربيع والخريف أكثر شيوعًا بقليل).
الجداول المتعلقة بسؤالك طويلة، لذا سأضعها في علامات حرق. انقر على الأزرار للاطلاع على الإجابات.
عيد ميلاد مشترك لشخصين أو أكثر
| حجم المجموعة | احتمال |
|---|---|
| 2 | 0.002740 |
| 3 | 0.008204 |
| 4 | 0.016356 |
| 5 | 0.027136 |
| 6 | 0.040462 |
| 7 | 0.056236 |
| 8 | 0.074335 |
| 9 | 0.094624 |
| 10 | 0.116948 |
| 11 | 0.141141 |
| 12 | 0.167025 |
| 13 | 0.194410 |
| 14 | 0.223103 |
| 15 | 0.252901 |
| 16 | 0.283604 |
| 17 | 0.315008 |
| 18 | 0.346911 |
| 19 | 0.379119 |
| 20 | 0.411438 |
| 21 | 0.443688 |
| 22 | 0.475695 |
| 23 | 0.507297 |
| 24 | 0.538344 |
| 25 | 0.568700 |
| 26 | 0.598241 |
| 27 | 0.626859 |
| 28 | 0.654461 |
| 29 | 0.680969 |
| 30 | 0.706316 |
| 31 | 0.730455 |
| 32 | 0.753348 |
| 33 | 0.774972 |
| 34 | 0.795317 |
| 35 | 0.814383 |
| 36 | 0.832182 |
| 37 | 0.848734 |
| 38 | 0.864068 |
| 39 | 0.878220 |
| 40 | 0.891232 |
| 41 | 0.903152 |
| 42 | 0.914030 |
| 43 | 0.923923 |
| 44 | 0.932885 |
| 45 | 0.940976 |
| 46 | 0.948253 |
| 47 | 0.954774 |
| 48 | 0.960598 |
| 49 | 0.965780 |
| 50 | 0.970374 |
| 51 | 0.974432 |
| 52 | 0.978005 |
| 53 | 0.981138 |
| 54 | 0.983877 |
| 55 | 0.986262 |
| 56 | 0.988332 |
| 57 | 0.990122 |
| 58 | 0.991665 |
| 59 | 0.992989 |
| 60 | 0.994123 |
| 61 | 0.995089 |
| 62 | 0.995910 |
| 63 | 0.996604 |
| 64 | 0.997190 |
| 65 | 0.997683 |
| 66 | 0.998096 |
| 67 | 0.998440 |
| 68 | 0.998726 |
| 69 | 0.998964 |
| 70 | 0.999160 |
| 71 | 0.999321 |
| 72 | 0.999453 |
| 73 | 0.999561 |
| 74 | 0.999649 |
| 75 | 0.999720 |
| 76 | 0.999777 |
| 77 | 0.999824 |
| 78 | 0.999861 |
| 79 | 0.999891 |
| 80 | 0.999914 |
| 81 | 0.999933 |
| 82 | 0.999948 |
| 83 | 0.999960 |
| 84 | 0.999969 |
عيد ميلاد مشترك لـ 3 أشخاص أو أكثر
| حجم المجموعة | احتمال |
|---|---|
| 3 | 0.000008 |
| 4 | 0.000030 |
| 5 | 0.000075 |
| 6 | 0.000149 |
| 7 | 0.000261 |
| 8 | 0.000416 |
| 9 | 0.000623 |
| 10 | 0.000888 |
| 11 | 0.001218 |
| 12 | 0.001621 |
| 13 | 0.002102 |
| 14 | 0.002670 |
| 15 | 0.003329 |
| 16 | 0.004088 |
| 17 | 0.004953 |
| 18 | 0.005929 |
| 19 | 0.007024 |
| 20 | 0.008243 |
| 21 | 0.009592 |
| 22 | 0.011078 |
| 23 | 0.012705 |
| 24 | 0.014481 |
| 25 | 0.016409 |
| 26 | 0.018497 |
| 27 | 0.020747 |
| 28 | 0.023167 |
| 29 | 0.025760 |
| 30 | 0.028531 |
| 31 | 0.031484 |
| 32 | 0.034624 |
| 33 | 0.037954 |
| 34 | 0.041479 |
| 35 | 0.045202 |
| 36 | 0.049126 |
| 37 | 0.053254 |
| 38 | 0.057589 |
| 39 | 0.062133 |
| 40 | 0.066889 |
| 41 | 0.071859 |
| 42 | 0.077044 |
| 43 | 0.082446 |
| 44 | 0.088065 |
| 45 | 0.093903 |
| 46 | 0.099960 |
| 47 | 0.106236 |
| 48 | 0.112731 |
| 49 | 0.119444 |
| 50 | 0.126375 |
| 51 | 0.133522 |
| 52 | 0.140885 |
| 53 | 0.148460 |
| 54 | 0.156246 |
| 55 | 0.164241 |
| 56 | 0.172441 |
| 57 | 0.180844 |
| 58 | 0.189445 |
| 59 | 0.198242 |
| 60 | 0.207230 |
| 61 | 0.216405 |
| 62 | 0.225761 |
| 63 | 0.235294 |
| 64 | 0.244999 |
| 65 | 0.254869 |
| 66 | 0.264899 |
| 67 | 0.275082 |
| 68 | 0.285413 |
| 69 | 0.295883 |
| 70 | 0.306487 |
| 71 | 0.317217 |
| 72 | 0.328066 |
| 73 | 0.339026 |
| 74 | 0.350088 |
| 75 | 0.361246 |
| 76 | 0.372491 |
| 77 | 0.383814 |
| 78 | 0.395207 |
| 79 | 0.406662 |
| 80 | 0.418169 |
| 81 | 0.429720 |
| 82 | 0.441307 |
| 83 | 0.452920 |
| 84 | 0.464550 |
| 85 | 0.476188 |
| 86 | 0.487826 |
| 87 | 0.499455 |
| 88 | 0.511065 |
| 89 | 0.522648 |
| 90 | 0.534196 |
| 91 | 0.545698 |
| 92 | 0.557148 |
| 93 | 0.568537 |
| 94 | 0.579855 |
| 95 | 0.591096 |
| 96 | 0.602252 |
| 97 | 0.613314 |
| 98 | 0.624275 |
| 99 | 0.635127 |
| 100 | 0.645865 |
| 101 | 0.656480 |
| 102 | 0.666967 |
| 103 | 0.677318 |
| 104 | 0.687529 |
| 105 | 0.697593 |
| 106 | 0.707505 |
| 107 | 0.717260 |
| 108 | 0.726853 |
| 109 | 0.736279 |
| 110 | 0.745536 |
| 111 | 0.754619 |
| 112 | 0.763525 |
| 113 | 0.772251 |
| 114 | 0.780795 |
| 115 | 0.789155 |
| 116 | 0.797330 |
| 117 | 0.805319 |
| 118 | 0.813121 |
| 119 | 0.820580 |
| 120 | 0.827964 |
| 121 | 0.835152 |
| 122 | 0.842144 |
| 123 | 0.848940 |
| 124 | 0.855540 |
| 125 | 0.861945 |
| 126 | 0.868155 |
| 127 | 0.874172 |
| 128 | 0.879996 |
| 129 | 0.885631 |
| 130 | 0.891076 |
| 131 | 0.896335 |
| 132 | 0.901409 |
| 133 | 0.906302 |
| 134 | 0.911015 |
| 135 | 0.915552 |
| 136 | 0.919915 |
| 137 | 0.924108 |
| 138 | 0.928135 |
| 139 | 0.931997 |
| 140 | 0.935700 |
| 141 | 0.939246 |
| 142 | 0.942640 |
| 143 | 0.945885 |
| 144 | 0.948985 |
| 145 | 0.951944 |
| 146 | 0.954766 |
| 147 | 0.957456 |
| 148 | 0.960016 |
| 149 | 0.962452 |
| 150 | 0.964767 |
| 151 | 0.966965 |
| 152 | 0.969050 |
| 153 | 0.971028 |
| 154 | 0.972900 |
| 155 | 0.974672 |
| 156 | 0.976347 |
| 157 | 0.977930 |
| 158 | 0.979423 |
| 159 | 0.980831 |
| 160 | 0.982158 |
| 161 | 0.983407 |
| 162 | 0.984581 |
| 163 | 0.985684 |
| 164 | 0.986719 |
| 165 | 0.987690 |
| 166 | 0.988600 |
| 167 | 0.989452 |
| 168 | 0.990248 |
| 169 | 0.990992 |
| 170 | 0.991687 |
| 171 | 0.992335 |
| 172 | 0.992938 |
| 173 | 0.993500 |
| 174 | 0.994022 |
| 175 | 0.994508 |
| 176 | 0.994958 |
| 177 | 0.995376 |
| 178 | 0.995763 |
| 179 | 0.996121 |
| 180 | 0.996452 |
| 181 | 0.996758 |
| 182 | 0.997040 |
| 183 | 0.997300 |
| 184 | 0.997540 |
| 185 | 0.997760 |
| 186 | 0.997963 |
| 187 | 0.998149 |
| 188 | 0.998319 |
| 189 | 0.998476 |
| 190 | 0.998619 |
| 191 | 0.998750 |
| 192 | 0.998869 |
| 193 | 0.998979 |
| 194 | 0.999078 |
| 195 | 0.999169 |
| 196 | 0.999251 |
| 197 | 0.999326 |
| 198 | 0.999394 |
| 199 | 0.999456 |
| 200 | 0.999512 |
| 201 | 0.999562 |
| 202 | 0.999608 |
| 203 | 0.999650 |
| 204 | 0.999687 |
| 205 | 0.999720 |
| 206 | 0.999751 |
| 207 | 0.999778 |
| 208 | 0.999802 |
| 209 | 0.999824 |
| 210 | 0.999844 |
| 211 | 0.999862 |
| 212 | 0.999877 |
| 213 | 0.999891 |
| 214 | 0.999904 |
| 215 | 0.999915 |
| 216 | 0.999925 |
| 217 | 0.999934 |
| 218 | 0.999942 |
| 219 | 0.999949 |
| 220 | 0.999955 |
| 221 | 0.999961 |
| 222 | 0.999966 |
| 223 | 0.999970 |
| 224 | 0.999974 |
| 225 | 0.999977 |
| 226 | 0.999980 |
| 227 | 0.999982 |
| 228 | 0.999985 |
| 229 | 0.999987 |
| 230 | 0.999988 |
| 231 | 0.999990 |
| 232 | 0.999991 |
| 233 | 0.999992 |
| 234 | 0.999994 |
| 235 | 0.999994 |
| 236 | 0.999995 |
| 237 | 0.999996 |
| 238 | 0.999996 |
| 239 | 0.999997 |
| 240 | 0.999997 |
| 241 | 0.999998 |
| 242 | 0.999998 |
| 243 | 0.999998 |
| 244 | 0.999999 |
عيد ميلاد مشترك لأربعة أشخاص أو أكثر
| حجم المجموعة | احتمال |
|---|---|
| 4 | 0.000000 |
| 5 | 0.000000 |
| 6 | 0.000000 |
| 7 | 0.000001 |
| 8 | 0.000001 |
| 9 | 0.000003 |
| 10 | 0.000004 |
| 11 | 0.000007 |
| 12 | 0.000010 |
| 13 | 0.000014 |
| 14 | 0.000020 |
| 15 | 0.000027 |
| 16 | 0.000036 |
| 17 | 0.000048 |
| 18 | 0.000061 |
| 19 | 0.000077 |
| 20 | 0.000096 |
| 21 | 0.000119 |
| 22 | 0.000145 |
| 23 | 0.000175 |
| 24 | 0.000209 |
| 25 | 0.000248 |
| 26 | 0.000293 |
| 27 | 0.000343 |
| 28 | 0.000399 |
| 29 | 0.000462 |
| 30 | 0.000532 |
| 31 | 0.000610 |
| 32 | 0.000695 |
| 33 | 0.000790 |
| 34 | 0.000893 |
| 35 | 0.001006 |
| 36 | 0.001129 |
| 37 | 0.001263 |
| 38 | 0.001408 |
| 39 | 0.001566 |
| 40 | 0.001736 |
| 41 | 0.001919 |
| 42 | 0.002116 |
| 43 | 0.002328 |
| 44 | 0.002555 |
| 45 | 0.002798 |
| 46 | 0.003058 |
| 47 | 0.003334 |
| 48 | 0.003629 |
| 49 | 0.003943 |
| 50 | 0.004276 |
| 51 | 0.004629 |
| 52 | 0.005003 |
| 53 | 0.005399 |
| 54 | 0.005817 |
| 55 | 0.006258 |
| 56 | 0.006724 |
| 57 | 0.007214 |
| 58 | 0.007730 |
| 59 | 0.008272 |
| 60 | 0.008841 |
| 61 | 0.009439 |
| 62 | 0.010065 |
| 63 | 0.010721 |
| 64 | 0.011408 |
| 65 | 0.012126 |
| 66 | 0.012876 |
| 67 | 0.013659 |
| 68 | 0.014476 |
| 69 | 0.015327 |
| 70 | 0.016215 |
| 71 | 0.017139 |
| 72 | 0.018100 |
| 73 | 0.019099 |
| 74 | 0.020137 |
| 75 | 0.021215 |
| 76 | 0.022334 |
| 77 | 0.023495 |
| 78 | 0.024698 |
| 79 | 0.025944 |
| 80 | 0.027235 |
| 81 | 0.028570 |
| 82 | 0.029951 |
| 83 | 0.031379 |
| 84 | 0.032855 |
| 85 | 0.034379 |
| 86 | 0.035952 |
| 87 | 0.037575 |
| 88 | 0.039249 |
| 89 | 0.040974 |
| 90 | 0.042752 |
| 91 | 0.044583 |
| 92 | 0.046467 |
| 93 | 0.048407 |
| 94 | 0.050402 |
| 95 | 0.052453 |
| 96 | 0.054561 |
| 97 | 0.056726 |
| 98 | 0.058950 |
| 99 | 0.061233 |
| 100 | 0.063576 |
| 101 | 0.065978 |
| 102 | 0.068442 |
| 103 | 0.070967 |
| 104 | 0.073554 |
| 105 | 0.076204 |
| 106 | 0.078917 |
| 107 | 0.081694 |
| 108 | 0.084535 |
| 109 | 0.087441 |
| 110 | 0.090412 |
| 111 | 0.093449 |
| 112 | 0.096552 |
| 113 | 0.099722 |
| 114 | 0.102958 |
| 115 | 0.106262 |
| 116 | 0.109633 |
| 117 | 0.113072 |
| 118 | 0.116579 |
| 119 | 0.120154 |
| 120 | 0.123798 |
| 121 | 0.127510 |
| 122 | 0.131292 |
| 123 | 0.135142 |
| 124 | 0.139061 |
| 125 | 0.143050 |
| 126 | 0.147107 |
| 127 | 0.151234 |
| 128 | 0.155429 |
| 129 | 0.159694 |
| 130 | 0.164027 |
| 131 | 0.168429 |
| 132 | 0.172899 |
| 133 | 0.177438 |
| 134 | 0.182044 |
| 135 | 0.186719 |
| 136 | 0.191460 |
| 137 | 0.196269 |
| 138 | 0.201144 |
| 139 | 0.206085 |
| 140 | 0.211091 |
| 141 | 0.216163 |
| 142 | 0.221299 |
| 143 | 0.226499 |
| 144 | 0.231763 |
| 145 | 0.237089 |
| 146 | 0.242476 |
| 147 | 0.247925 |
| 148 | 0.253434 |
| 149 | 0.259002 |
| 150 | 0.264629 |
| 151 | 0.270314 |
| 152 | 0.276055 |
| 153 | 0.281852 |
| 154 | 0.287703 |
| 155 | 0.293608 |
| 156 | 0.299566 |
| 157 | 0.305575 |
| 158 | 0.311634 |
| 159 | 0.317741 |
| 160 | 0.323897 |
| 161 | 0.330099 |
| 162 | 0.336346 |
| 163 | 0.342637 |
| 164 | 0.348970 |
| 165 | 0.355343 |
| 166 | 0.361757 |
| 167 | 0.368208 |
| 168 | 0.374696 |
| 169 | 0.381218 |
| 170 | 0.387774 |
| 171 | 0.394362 |
| 172 | 0.400980 |
| 173 | 0.407626 |
| 174 | 0.414299 |
| 175 | 0.420997 |
| 176 | 0.427718 |
| 177 | 0.434462 |
| 178 | 0.441224 |
| 179 | 0.448005 |
| 180 | 0.454803 |
| 181 | 0.461615 |
| 182 | 0.468439 |
| 183 | 0.475274 |
| 184 | 0.482118 |
| 185 | 0.488969 |
| 186 | 0.495826 |
| 187 | 0.502685 |
| 188 | 0.509546 |
| 189 | 0.516407 |
| 190 | 0.523265 |
| 191 | 0.530119 |
| 192 | 0.536967 |
| 193 | 0.543807 |
| 194 | 0.550636 |
| 195 | 0.557454 |
| 196 | 0.564258 |
| 197 | 0.571046 |
| 198 | 0.577817 |
| 199 | 0.584568 |
| 200 | 0.591298 |
| 201 | 0.598005 |
| 202 | 0.604687 |
| 203 | 0.611342 |
| 204 | 0.617969 |
| 205 | 0.624565 |
| 206 | 0.631129 |
| 207 | 0.637659 |
| 208 | 0.644154 |
| 209 | 0.650611 |
| 210 | 0.657030 |
| 211 | 0.663407 |
| 212 | 0.669743 |
| 213 | 0.676035 |
| 214 | 0.682281 |
| 215 | 0.688481 |
| 216 | 0.694632 |
| 217 | 0.700734 |
| 218 | 0.706784 |
| 219 | 0.712782 |
| 220 | 0.718726 |
| 221 | 0.724614 |
| 222 | 0.730446 |
| 223 | 0.736220 |
| 224 | 0.741936 |
| 225 | 0.747591 |
| 226 | 0.753185 |
| 227 | 0.758717 |
| 228 | 0.764185 |
| 229 | 0.769590 |
| 230 | 0.774929 |
| 231 | 0.780202 |
| 232 | 0.785409 |
| 233 | 0.790547 |
| 234 | 0.795618 |
| 235 | 0.800619 |
| 236 | 0.805551 |
| 237 | 0.810412 |
| 238 | 0.815202 |
| 239 | 0.819921 |
| 240 | 0.824569 |
| 241 | 0.829144 |
| 242 | 0.833646 |
| 243 | 0.838076 |
| 244 | 0.842432 |
| 245 | 0.846716 |
| 246 | 0.850925 |
| 247 | 0.855061 |
| 248 | 0.859123 |
| 249 | 0.863112 |
| 250 | 0.867027 |
| 251 | 0.870868 |
| 252 | 0.874635 |
| 253 | 0.878329 |
| 254 | 0.881950 |
| 255 | 0.885498 |
| 256 | 0.888973 |
| 257 | 0.892375 |
| 258 | 0.895705 |
| 259 | 0.898964 |
| 260 | 0.902151 |
| 261 | 0.905268 |
| 262 | 0.908314 |
| 263 | 0.911290 |
| 264 | 0.914197 |
| 265 | 0.917036 |
| 266 | 0.919806 |
| 267 | 0.922509 |
| 268 | 0.925145 |
| 269 | 0.927715 |
| 270 | 0.930220 |
| 271 | 0.932661 |
| 272 | 0.935037 |
| 273 | 0.937351 |
| 274 | 0.939603 |
| 275 | 0.941793 |
| 276 | 0.943923 |
| 277 | 0.945993 |
| 278 | 0.948005 |
| 279 | 0.949960 |
| 280 | 0.951857 |
| 281 | 0.953699 |
| 282 | 0.955486 |
| 283 | 0.957218 |
| 284 | 0.958898 |
| 285 | 0.960527 |
| 286 | 0.962104 |
| 287 | 0.963631 |
| 288 | 0.965109 |
| 289 | 0.966540 |
| 290 | 0.967923 |
| 291 | 0.969260 |
| 292 | 0.970553 |
| 293 | 0.971802 |
| 294 | 0.973007 |
| 295 | 0.974171 |
| 296 | 0.975294 |
| 297 | 0.976377 |
| 298 | 0.977421 |
| 299 | 0.978427 |
| 300 | 0.979397 |
| 301 | 0.980330 |
| 302 | 0.981228 |
| 303 | 0.982092 |
| 304 | 0.982923 |
| 305 | 0.983722 |
| 306 | 0.984490 |
| 307 | 0.985227 |
| 308 | 0.985935 |
| 309 | 0.986614 |
| 310 | 0.987266 |
| 311 | 0.987890 |
| 312 | 0.988489 |
| 313 | 0.989063 |
| 314 | 0.989612 |
| 315 | 0.990138 |
| 316 | 0.990641 |
| 317 | 0.991122 |
| 318 | 0.991581 |
| 319 | 0.992021 |
| 320 | 0.992440 |
| 321 | 0.992841 |
| 322 | 0.993223 |
| 323 | 0.993587 |
| 324 | 0.993935 |
| 325 | 0.994266 |
| 326 | 0.994581 |
| 327 | 0.994882 |
| 328 | 0.995167 |
| 329 | 0.995439 |
| 330 | 0.995698 |
| 331 | 0.995943 |
| 332 | 0.996176 |
| 333 | 0.996398 |
| 334 | 0.996608 |
| 335 | 0.996807 |
| 336 | 0.996996 |
| 337 | 0.997175 |
| 338 | 0.997344 |
| 339 | 0.997505 |
| 340 | 0.997657 |
| 341 | 0.997801 |
| 342 | 0.997936 |
| 343 | 0.998065 |
| 344 | 0.998186 |
| 345 | 0.998300 |
| 346 | 0.998408 |
| 347 | 0.998510 |
| 348 | 0.998606 |
| 349 | 0.998696 |
| 350 | 0.998781 |
| 351 | 0.998861 |
| 352 | 0.998937 |
| 353 | 0.999008 |
| 354 | 0.999074 |
| 355 | 0.999137 |
| 356 | 0.999195 |
| 357 | 0.999250 |
| 358 | 0.999302 |
| 359 | 0.999350 |
| 360 | 0.999396 |
| 361 | 0.999438 |
| 362 | 0.999478 |
| 363 | 0.999515 |
| 364 | 0.999550 |
| 365 | 0.999582 |
| 366 | 0.999613 |
| 367 | 0.999641 |
| 368 | 0.999668 |
| 369 | 0.999692 |
| 370 | 0.999715 |
| 371 | 0.999736 |
| 372 | 0.999756 |
| 373 | 0.999775 |
| 374 | 0.999792 |
| 375 | 0.999808 |
| 376 | 0.999823 |
| 377 | 0.999837 |
| 378 | 0.999850 |
| 379 | 0.999861 |
| 380 | 0.999872 |
| 381 | 0.999883 |
| 382 | 0.999892 |
| 383 | 0.999901 |
| 384 | 0.999909 |
| 385 | 0.999916 |
| 386 | 0.999923 |
| 387 | 0.999930 |
| 388 | 0.999935 |
| 389 | 0.999941 |
| 390 | 0.999946 |
| 391 | 0.999950 |
| 392 | 0.999955 |
| 393 | 0.999959 |
| 394 | 0.999962 |
| 395 | 0.999965 |
| 396 | 0.999969 |
| 397 | 0.999971 |
| 398 | 0.999974 |
| 399 | 0.999976 |
| 400 | 0.999978 |
| 401 | 0.999980 |
| 402 | 0.999982 |
| 403 | 0.999984 |
| 404 | 0.999985 |
| 405 | 0.999987 |
| 406 | 0.999988 |
| 407 | 0.999989 |
| 408 | 0.999990 |
| 409 | 0.999991 |
| 410 | 0.999992 |
| 411 | 0.999993 |
| 412 | 0.999993 |
| 413 | 0.999994 |
| 414 | 0.999995 |
| 415 | 0.999995 |
| 416 | 0.999996 |
| 417 | 0.999996 |
| 418 | 0.999996 |
| 419 | 0.999997 |
| 420 | 0.999997 |
| 421 | 0.999997 |
| 422 | 0.999998 |
| 423 | 0.999998 |
| 424 | 0.999998 |
| 425 | 0.999998 |
| 426 | 0.999998 |
| 427 | 0.999999 |
| 428 | 0.999999 |
| 429 | 0.999999 |
عيد ميلاد مشترك لخمسة أشخاص أو أكثر
| حجم المجموعة | احتمال |
|---|---|
| 5 | 0.000000 |
| 6 | 0.000000 |
| 7 | 0.000000 |
| 8 | 0.000000 |
| 9 | 0.000000 |
| 10 | 0.000000 |
| 11 | 0.000000 |
| 12 | 0.000000 |
| 13 | 0.000000 |
| 14 | 0.000000 |
| 15 | 0.000000 |
| 16 | 0.000000 |
| 17 | 0.000000 |
| 18 | 0.000001 |
| 19 | 0.000001 |
| 20 | 0.000001 |
| 21 | 0.000001 |
| 22 | 0.000002 |
| 23 | 0.000002 |
| 24 | 0.000003 |
| 25 | 0.000004 |
| 26 | 0.000004 |
| 27 | 0.000005 |
| 28 | 0.000006 |
| 29 | 0.000008 |
| 30 | 0.000009 |
| 31 | 0.000011 |
| 32 | 0.000013 |
| 33 | 0.000015 |
| 34 | 0.000017 |
| 35 | 0.000020 |
| 36 | 0.000023 |
| 37 | 0.000026 |
| 38 | 0.000030 |
| 39 | 0.000034 |
| 40 | 0.000039 |
| 41 | 0.000044 |
| 42 | 0.000050 |
| 43 | 0.000056 |
| 44 | 0.000063 |
| 45 | 0.000070 |
| 46 | 0.000079 |
| 47 | 0.000087 |
| 48 | 0.000097 |
| 49 | 0.000108 |
| 50 | 0.000119 |
| 51 | 0.000132 |
| 52 | 0.000145 |
| 53 | 0.000159 |
| 54 | 0.000175 |
| 55 | 0.000192 |
| 56 | 0.000209 |
| 57 | 0.000229 |
| 58 | 0.000249 |
| 59 | 0.000271 |
| 60 | 0.000295 |
| 61 | 0.000320 |
| 62 | 0.000347 |
| 63 | 0.000375 |
| 64 | 0.000406 |
| 65 | 0.000438 |
| 66 | 0.000472 |
| 67 | 0.000509 |
| 68 | 0.000547 |
| 69 | 0.000588 |
| 70 | 0.000631 |
| 71 | 0.000676 |
| 72 | 0.000725 |
| 73 | 0.000775 |
| 74 | 0.000829 |
| 75 | 0.000885 |
| 76 | 0.000944 |
| 77 | 0.001007 |
| 78 | 0.001072 |
| 79 | 0.001141 |
| 80 | 0.001213 |
| 81 | 0.001289 |
| 82 | 0.001369 |
| 83 | 0.001452 |
| 84 | 0.001539 |
| 85 | 0.001630 |
| 86 | 0.001726 |
| 87 | 0.001825 |
| 88 | 0.001930 |
| 89 | 0.002038 |
| 90 | 0.002152 |
| 91 | 0.002270 |
| 92 | 0.002394 |
| 93 | 0.002522 |
| 94 | 0.002656 |
| 95 | 0.002796 |
| 96 | 0.002941 |
| 97 | 0.003092 |
| 98 | 0.003249 |
| 99 | 0.003412 |
| 100 | 0.003581 |
| 101 | 0.003757 |
| 102 | 0.003939 |
| 103 | 0.004128 |
| 104 | 0.004325 |
| 105 | 0.004528 |
| 106 | 0.004739 |
| 107 | 0.004957 |
| 108 | 0.005183 |
| 109 | 0.005417 |
| 110 | 0.005659 |
| 111 | 0.005909 |
| 112 | 0.006168 |
| 113 | 0.006436 |
| 114 | 0.006712 |
| 115 | 0.006998 |
| 116 | 0.007293 |
| 117 | 0.007597 |
| 118 | 0.007912 |
| 119 | 0.008236 |
| 120 | 0.008570 |
| 121 | 0.008915 |
| 122 | 0.009270 |
| 123 | 0.009636 |
| 124 | 0.010013 |
| 125 | 0.010402 |
| 126 | 0.010801 |
| 127 | 0.011213 |
| 128 | 0.011637 |
| 129 | 0.012072 |
| 130 | 0.012521 |
| 131 | 0.012981 |
| 132 | 0.013455 |
| 133 | 0.013942 |
| 134 | 0.014442 |
| 135 | 0.014956 |
| 136 | 0.015484 |
| 137 | 0.016026 |
| 138 | 0.016582 |
| 139 | 0.017153 |
| 140 | 0.017739 |
| 141 | 0.018340 |
| 142 | 0.018956 |
| 143 | 0.019588 |
| 144 | 0.020235 |
| 145 | 0.020899 |
| 146 | 0.021580 |
| 147 | 0.022277 |
| 148 | 0.022991 |
| 149 | 0.023722 |
| 150 | 0.024470 |
| 151 | 0.025237 |
| 152 | 0.026021 |
| 153 | 0.026824 |
| 154 | 0.027645 |
| 155 | 0.028485 |
| 156 | 0.029344 |
| 157 | 0.030222 |
| 158 | 0.031120 |
| 159 | 0.032037 |
| 160 | 0.032975 |
| 161 | 0.033934 |
| 162 | 0.034913 |
| 163 | 0.035912 |
| 164 | 0.036934 |
| 165 | 0.037976 |
| 166 | 0.039040 |
| 167 | 0.040127 |
| 168 | 0.041235 |
| 169 | 0.042367 |
| 170 | 0.043521 |
| 171 | 0.044698 |
| 172 | 0.045898 |
| 173 | 0.047122 |
| 174 | 0.048370 |
| 175 | 0.049642 |
| 176 | 0.050939 |
| 177 | 0.052260 |
| 178 | 0.053606 |
| 179 | 0.054977 |
| 180 | 0.056374 |
| 181 | 0.057796 |
| 182 | 0.059245 |
| 183 | 0.060719 |
| 184 | 0.062220 |
| 185 | 0.063748 |
| 186 | 0.065302 |
| 187 | 0.066884 |
| 188 | 0.068493 |
| 189 | 0.070130 |
| 190 | 0.071795 |
| 191 | 0.073487 |
| 192 | 0.075209 |
| 193 | 0.076958 |
| 194 | 0.078737 |
| 195 | 0.080544 |
| 196 | 0.082381 |
| 197 | 0.084247 |
| 198 | 0.086143 |
| 199 | 0.088068 |
| 200 | 0.090024 |
| 201 | 0.092009 |
| 202 | 0.094026 |
| 203 | 0.096072 |
| 204 | 0.098150 |
| 205 | 0.100259 |
| 206 | 0.102398 |
| 207 | 0.104569 |
| 208 | 0.106772 |
| 209 | 0.109006 |
| 210 | 0.111272 |
| 211 | 0.113570 |
| 212 | 0.115899 |
| 213 | 0.118262 |
| 214 | 0.120656 |
| 215 | 0.123083 |
| 216 | 0.125542 |
| 217 | 0.128035 |
| 218 | 0.130559 |
| 219 | 0.133117 |
| 220 | 0.135708 |
| 221 | 0.138332 |
| 222 | 0.140989 |
| 223 | 0.143679 |
| 224 | 0.146403 |
| 225 | 0.149160 |
| 226 | 0.151950 |
| 227 | 0.154774 |
| 228 | 0.157632 |
| 229 | 0.160522 |
| 230 | 0.163447 |
| 231 | 0.166405 |
| 232 | 0.169396 |
| 233 | 0.172421 |
| 234 | 0.175480 |
| 235 | 0.178572 |
| 236 | 0.181698 |
| 237 | 0.184857 |
| 238 | 0.188049 |
| 239 | 0.191275 |
| 240 | 0.194534 |
| 241 | 0.197827 |
| 242 | 0.201152 |
| 243 | 0.204511 |
| 244 | 0.207902 |
| 245 | 0.211327 |
| 246 | 0.214784 |
| 247 | 0.218274 |
| 248 | 0.221796 |
| 249 | 0.225351 |
| 250 | 0.228937 |
| 251 | 0.232556 |
| 252 | 0.236207 |
| 253 | 0.239889 |
| 254 | 0.243603 |
| 255 | 0.247348 |
| 256 | 0.251124 |
| 257 | 0.254931 |
| 258 | 0.258768 |
| 259 | 0.262636 |
| 260 | 0.266534 |
| 261 | 0.270462 |
| 262 | 0.274419 |
| 263 | 0.278406 |
| 264 | 0.282422 |
| 265 | 0.286466 |
| 266 | 0.290539 |
| 267 | 0.294639 |
| 268 | 0.298768 |
| 269 | 0.302924 |
| 270 | 0.307106 |
| 271 | 0.311316 |
| 272 | 0.315551 |
| 273 | 0.319813 |
| 274 | 0.324100 |
| 275 | 0.328412 |
| 276 | 0.332749 |
| 277 | 0.337110 |
| 278 | 0.341495 |
| 279 | 0.345903 |
| 280 | 0.350334 |
| 281 | 0.354788 |
| 282 | 0.359264 |
| 283 | 0.363761 |
| 284 | 0.368279 |
| 285 | 0.372818 |
| 286 | 0.377376 |
| 287 | 0.381955 |
| 288 | 0.386552 |
| 289 | 0.391167 |
| 290 | 0.395801 |
| 291 | 0.400452 |
| 292 | 0.405119 |
| 293 | 0.409803 |
| 294 | 0.414503 |
| 295 | 0.419217 |
| 296 | 0.423946 |
| 297 | 0.428689 |
| 298 | 0.433445 |
| 299 | 0.438214 |
| 300 | 0.442995 |
| 301 | 0.447787 |
| 302 | 0.452590 |
| 303 | 0.457403 |
| 304 | 0.462226 |
| 305 | 0.467057 |
| 306 | 0.471897 |
| 307 | 0.476744 |
| 308 | 0.481599 |
| 309 | 0.486459 |
| 310 | 0.491325 |
| 311 | 0.496196 |
| 312 | 0.501070 |
| 313 | 0.505949 |
| 314 | 0.510830 |
| 315 | 0.515713 |
| 316 | 0.520598 |
| 317 | 0.525483 |
| 318 | 0.530369 |
| 319 | 0.535253 |
| 320 | 0.540137 |
| 321 | 0.545018 |
| 322 | 0.549896 |
| 323 | 0.554771 |
| 324 | 0.559642 |
| 325 | 0.564507 |
| 326 | 0.569367 |
| 327 | 0.574221 |
| 328 | 0.579067 |
| 329 | 0.583906 |
| 330 | 0.588736 |
| 331 | 0.593557 |
| 332 | 0.598368 |
| 333 | 0.603169 |
| 334 | 0.607958 |
| 335 | 0.612735 |
| 336 | 0.617500 |
| 337 | 0.622251 |
| 338 | 0.626988 |
| 339 | 0.631710 |
| 340 | 0.636417 |
| 341 | 0.641107 |
| 342 | 0.645781 |
| 343 | 0.650437 |
| 344 | 0.655075 |
| 345 | 0.659695 |
| 346 | 0.664295 |
| 347 | 0.668875 |
| 348 | 0.673434 |
| 349 | 0.677972 |
| 350 | 0.682488 |
| 351 | 0.686981 |
| 352 | 0.691451 |
| 353 | 0.695897 |
| 354 | 0.700319 |
| 355 | 0.704716 |
| 356 | 0.709088 |
| 357 | 0.713433 |
| 358 | 0.717752 |
| 359 | 0.722043 |
| 360 | 0.726307 |
| 361 | 0.730543 |
| 362 | 0.734750 |
| 363 | 0.738927 |
| 364 | 0.743075 |
| 365 | 0.747193 |
| 366 | 0.751279 |
| 367 | 0.755335 |
| 368 | 0.759359 |
| 369 | 0.763351 |
| 370 | 0.767310 |
| 371 | 0.771237 |
| 372 | 0.775130 |
| 373 | 0.778990 |
| 374 | 0.782815 |
| 375 | 0.786606 |
| 376 | 0.790363 |
| 377 | 0.794084 |
| 378 | 0.797770 |
| 379 | 0.801420 |
| 380 | 0.805034 |
| 381 | 0.808611 |
| 382 | 0.812152 |
| 383 | 0.815656 |
| 384 | 0.819123 |
| 385 | 0.822553 |
| 386 | 0.825945 |
| 387 | 0.829300 |
| 388 | 0.832616 |
| 389 | 0.835895 |
| 390 | 0.839135 |
| 391 | 0.842336 |
| 392 | 0.845499 |
| 393 | 0.848624 |
| 394 | 0.851709 |
| 395 | 0.854756 |
| 396 | 0.857764 |
| 397 | 0.860733 |
| 398 | 0.863663 |
| 399 | 0.866553 |
| 400 | 0.869405 |
| 401 | 0.872217 |
| 402 | 0.874990 |
| 403 | 0.877724 |
| 404 | 0.880419 |
| 405 | 0.883075 |
| 406 | 0.885692 |
| 407 | 0.888269 |
| 408 | 0.890808 |
| 409 | 0.893309 |
| 410 | 0.895770 |
| 411 | 0.898193 |
| 412 | 0.900578 |
| 413 | 0.902924 |
| 414 | 0.905232 |
| 415 | 0.907502 |
| 416 | 0.909734 |
| 417 | 0.911929 |
| 418 | 0.914086 |
| 419 | 0.916205 |
| 420 | 0.918288 |
| 421 | 0.920334 |
| 422 | 0.922344 |
| 423 | 0.924317 |
| 424 | 0.926254 |
| 425 | 0.928155 |
| 426 | 0.930020 |
| 427 | 0.931851 |
| 428 | 0.933646 |
| 429 | 0.935406 |
| 430 | 0.937133 |
| 431 | 0.938825 |
| 432 | 0.940483 |
| 433 | 0.942108 |
| 434 | 0.943699 |
| 435 | 0.945258 |
| 436 | 0.946785 |
| 437 | 0.948279 |
| 438 | 0.949741 |
| 439 | 0.951173 |
| 440 | 0.952573 |
| 441 | 0.953942 |
| 442 | 0.955281 |
| 443 | 0.956590 |
| 444 | 0.957870 |
| 445 | 0.959120 |
| 446 | 0.960342 |
| 447 | 0.961535 |
| 448 | 0.962701 |
| 449 | 0.963838 |
| 450 | 0.964949 |
| 451 | 0.966032 |
| 452 | 0.967090 |
| 453 | 0.968121 |
| 454 | 0.969127 |
| 455 | 0.970107 |
| 456 | 0.971063 |
| 457 | 0.971994 |
| 458 | 0.972902 |
| 459 | 0.973785 |
| 460 | 0.974646 |
| 461 | 0.975484 |
| 462 | 0.976299 |
| 463 | 0.977093 |
| 464 | 0.977865 |
| 465 | 0.978616 |
| 466 | 0.979346 |
| 467 | 0.980056 |
| 468 | 0.980746 |
| 469 | 0.981416 |
| 470 | 0.982067 |
| 471 | 0.982699 |
| 472 | 0.983313 |
| 473 | 0.983909 |
| 474 | 0.984488 |
| 475 | 0.985049 |
| 476 | 0.985593 |
| 477 | 0.986121 |
| 478 | 0.986633 |
| 479 | 0.987128 |
| 480 | 0.987609 |
| 481 | 0.988074 |
| 482 | 0.988525 |
| 483 | 0.988962 |
| 484 | 0.989384 |
| 485 | 0.989793 |
| 486 | 0.990189 |
| 487 | 0.990571 |
| 488 | 0.990941 |
| 489 | 0.991299 |
| 490 | 0.991644 |
| 491 | 0.991978 |
| 492 | 0.992301 |
| 493 | 0.992612 |
| 494 | 0.992913 |
| 495 | 0.993203 |
| 496 | 0.993483 |
| 497 | 0.993753 |
| 498 | 0.994013 |
| 499 | 0.994264 |
| 500 | 0.994506 |
| 501 | 0.994740 |
| 502 | 0.994964 |
| 503 | 0.995180 |
| 504 | 0.995389 |
| 505 | 0.995589 |
| 506 | 0.995782 |
| 507 | 0.995967 |
| 508 | 0.996146 |
| 509 | 0.996317 |
| 510 | 0.996482 |
| 511 | 0.996640 |
| 512 | 0.996793 |
| 513 | 0.996939 |
| 514 | 0.997079 |
| 515 | 0.997213 |
| 516 | 0.997343 |
| 517 | 0.997466 |
| 518 | 0.997585 |
| 519 | 0.997699 |
| 520 | 0.997808 |
| 521 | 0.997913 |
| 522 | 0.998013 |
| 523 | 0.998109 |
| 524 | 0.998200 |
| 525 | 0.998288 |
| 526 | 0.998372 |
| 527 | 0.998452 |
| 528 | 0.998529 |
| 529 | 0.998602 |
| 530 | 0.998673 |
| 531 | 0.998739 |
| 532 | 0.998803 |
| 533 | 0.998864 |
| 534 | 0.998923 |
| 535 | 0.998978 |
| 536 | 0.999031 |
| 537 | 0.999082 |
| 538 | 0.999130 |
| 539 | 0.999176 |
| 540 | 0.999219 |
| 541 | 0.999261 |
| 542 | 0.999301 |
| 543 | 0.999338 |
| 544 | 0.999374 |
| 545 | 0.999408 |
| 546 | 0.999441 |
| 547 | 0.999471 |
| 548 | 0.999501 |
| 549 | 0.999528 |
| 550 | 0.999555 |
| 551 | 0.999580 |
| 552 | 0.999604 |
| 553 | 0.999626 |
| 554 | 0.999648 |
| 555 | 0.999668 |
| 556 | 0.999687 |
| 557 | 0.999705 |
| 558 | 0.999722 |
| 559 | 0.999739 |
| 560 | 0.999754 |
| 561 | 0.999769 |
| 562 | 0.999782 |
| 563 | 0.999795 |
| 564 | 0.999808 |
| 565 | 0.999819 |
| 566 | 0.999830 |
| 567 | 0.999841 |
| 568 | 0.999851 |
| 569 | 0.999860 |
| 570 | 0.999868 |
| 571 | 0.999877 |
| 572 | 0.999884 |
| 573 | 0.999892 |
| 574 | 0.999899 |
| 575 | 0.999905 |
| 576 | 0.999911 |
| 577 | 0.999917 |
| 578 | 0.999922 |
| 579 | 0.999927 |
| 580 | 0.999932 |
| 581 | 0.999936 |
| 582 | 0.999941 |
| 583 | 0.999945 |
| 584 | 0.999948 |
| 585 | 0.999952 |
| 586 | 0.999955 |
| 587 | 0.999958 |
| 588 | 0.999961 |
| 589 | 0.999964 |
| 590 | 0.999966 |
| 591 | 0.999968 |
| 592 | 0.999971 |
| 593 | 0.999973 |
| 594 | 0.999975 |
| 595 | 0.999976 |
| 596 | 0.999978 |
| 597 | 0.999980 |
| 598 | 0.999981 |
| 599 | 0.999982 |
| 600 | 0.999984 |
| 601 | 0.999985 |
| 602 | 0.999986 |
| 603 | 0.999987 |
| 604 | 0.999988 |
| 605 | 0.999989 |
| 606 | 0.999990 |
| 607 | 0.999990 |
| 608 | 0.999991 |
| 609 | 0.999992 |
| 610 | 0.999992 |
| 611 | 0.999993 |
| 612 | 0.999994 |
| 613 | 0.999994 |
| 614 | 0.999994 |
| 615 | 0.999995 |
| 616 | 0.999995 |
| 617 | 0.999996 |
| 618 | 0.999996 |
| 619 | 0.999996 |
| 620 | 0.999997 |
| 621 | 0.999997 |
| 622 | 0.999997 |
| 623 | 0.999997 |
| 624 | 0.999998 |
| 625 | 0.999998 |
| 626 | 0.999998 |
| 627 | 0.999998 |
| 628 | 0.999998 |
| 629 | 0.999998 |
| 630 | 0.999999 |
| 631 | 0.999999 |
| 632 | 0.999999 |
| 633 | 0.999999 |
| 634 | 0.999999 |
لنفترض أن لدى الموزع رقائق من جميع الفئات، قابلة للقسمة بالتساوي على دولار واحد. أنت تشتري على الطاولة بـ 10 دولارات. بكم طريقة مختلفة يمكن للموزع دفع الباقي مقابل الـ 10 دولارات؟ ماذا عن مبالغ الشراء الأخرى؟
هناك 42 طريقة يمكن للتاجر من خلالها توزيع أرباح بقيمة 10 دولارات. إليك هذه الطرق:
9,1
8,2
8،1،1
7,3
7،2،1
7،1،1،1
6,4
6،3،1
6،2،2
6،2،1،1
6،1،1،1،1
5,5
5،4،1
5،3،2
5،3،1،1
5،2،2،1
5،2،1،1،1
5،1،1،1،1،1
4،4،2
4،4،1،1
4،3،3
4،3،2،1
4،3،1،1،1
4،2،2،2
4،2،2،1،1
4،2،1،1،1،1
4،1،1،1،1،1،1
3،3،3،1
3،3،2،2
3،3،2،1،1
3،3،1،1،1،1
3،2،2،2،1
3،2،2،1،1،1
3،2،1،1،1،1،1
3،1،1،1،1،1،1،1،1
2،2،2،2،2
2،2،2،2،1،1
2،2،2،1،1،1،1
2،2،1،1،1،1،1،1
2،1،1،1،1،1،1،1،1،1
1,1,1,1,1,1,1,1,1,1,1
يُطلق علماء الرياضيات على هذه الأقسام اسم "الأقسام". هذا هو عدد الأقسام للكميات الابتدائية حتى 405، وهو أقصى ما يستطيع حاسوبي حسابه (2^64).
عيد ميلاد مشترك لشخصين أو أكثر
<!--/عنوان-الصندوق-->| أولي كمية | المجموع الأقسام |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 7 |
| 6 | 11 |
| 7 | 15 |
| 8 | 22 |
| 9 | 30 |
| 10 | 42 |
| 11 | 56 |
| 12 | 77 |
| 13 | 101 |
| 14 | 135 |
| 15 | 176 |
| 16 | 231 |
| 17 | 297 |
| 18 | 385 |
| 19 | 490 |
| 20 | 627 |
| 21 | 792 |
| 22 | 1002 |
| 23 | 1255 |
| 24 | 1575 |
| 25 | 1958 |
| 26 | 2436 |
| 27 | 3010 |
| 28 | 3718 |
| 29 | 4565 |
| 30 | 5604 |
| 31 | 6842 |
| 32 | 8349 |
| 33 | 10143 |
| 34 | 12310 |
| 35 | 14883 |
| 36 | 17977 |
| 37 | 21637 |
| 38 | 26015 |
| 39 | 31185 |
| 40 | 37338 |
| 41 | 44583 |
| 42 | 53174 |
| 43 | 63261 |
| 44 | 75175 |
| 45 | 89134 |
| 46 | 105558 |
| 47 | 124754 |
| 48 | 147273 |
| 49 | 173525 |
| 50 | 204226 |
| 51 | 239943 |
| 52 | 281589 |
| 53 | 329931 |
| 54 | 386155 |
| 55 | 451276 |
| 56 | 526823 |
| 57 | 614154 |
| 58 | 715220 |
| 59 | 831820 |
| 60 | 966467 |
| 61 | 1121505 |
| 62 | 1300156 |
| 63 | 1505499 |
| 64 | 1741630 |
| 65 | 2012558 |
| 66 | 2323520 |
| 67 | 2679689 |
| 68 | 3087735 |
| 69 | 3554345 |
| 70 | 4087968 |
| 71 | 4697205 |
| 72 | 5392783 |
| 73 | 6185689 |
| 74 | 7089500 |
| 75 | 8118264 |
| 76 | 9289091 |
| 77 | 10619863 |
| 78 | 12132164 |
| 79 | 13848650 |
| 80 | 15796476 |
| 81 | 18004327 |
| 82 | 20506255 |
| 83 | 23338469 |
| 84 | 26543660 |
| 85 | 30167357 |
| 86 | 34262962 |
| 87 | 38887673 |
| 88 | 44108109 |
| 89 | 49995925 |
| 90 | 56634173 |
| 91 | 64112359 |
| 92 | 72533807 |
| 93 | 82010177 |
| 94 | 92669720 |
| 95 | 104651419 |
| 96 | 118114304 |
| 97 | 133230930 |
| 98 | 150198136 |
| 99 | 169229875 |
| 100 | 190569292 |
| 101 | 214481126 |
| 102 | 241265379 |
| 103 | 271248950 |
| 104 | 304801365 |
| 105 | 342325709 |
| 106 | 384276336 |
| 107 | 431149389 |
| 108 | 483502844 |
| 109 | 541946240 |
| 110 | 607163746 |
| 111 | 679903203 |
| 112 | 761002156 |
| 113 | 851376628 |
| 114 | 952050665 |
| 115 | 1064144451 |
| 116 | 1188908248 |
| 117 | 1327710076 |
| 118 | 1482074143 |
| 119 | 1653668665 |
| 120 | 1844349560 |
| 121 | 2056148051 |
| 122 | 2291320912 |
| 123 | 2552338241 |
| 124 | 2841940500 |
| 125 | 3163127352 |
| 126 | 3519222692 |
| 127 | 3913864295 |
| 128 | 4351078600 |
| 129 | 4835271870 |
| 130 | 5371315400 |
| 131 | 5964539504 |
| 132 | 6620830889 |
| 133 | 7346629512 |
| 134 | 8149040695 |
| 135 | 9035836076 |
| 136 | 10015581680 |
| 137 | 11097645016 |
| 138 | 12292341831 |
| 139 | 13610949895 |
| 140 | 15065878135 |
| 141 | 16670689208 |
| 142 | 18440293320 |
| 143 | 20390982757 |
| 144 | 22540654445 |
| 145 | 24908858009 |
| 146 | 27517052599 |
| 147 | 30388671978 |
| 148 | 33549419497 |
| 149 | 37027355200 |
| 150 | 40853235313 |
| 151 | 45060624582 |
| 152 | 49686288421 |
| 153 | 54770336324 |
| 154 | 60356673280 |
| 155 | 66493182097 |
| 156 | 73232243759 |
| 157 | 80630964769 |
| 158 | 88751778802 |
| 159 | 97662728555 |
| 160 | 107438159466 |
| 161 | 118159068427 |
| 162 | 129913904637 |
| 163 | 142798995930 |
| 164 | 156919475295 |
| 165 | 172389800255 |
| 166 | 189334822579 |
| 167 | 207890420102 |
| 168 | 228204732751 |
| 169 | 250438925115 |
| 170 | 274768617130 |
| 171 | 301384802048 |
| 172 | 330495499613 |
| 173 | 362326859895 |
| 174 | 397125074750 |
| 175 | 435157697830 |
| 176 | 476715857290 |
| 177 | 522115831195 |
| 178 | 571701605655 |
| 179 | 625846753120 |
| 180 | 684957390936 |
| 181 | 749474411781 |
| 182 | 819876908323 |
| 183 | 896684817527 |
| 184 | 980462880430 |
| 185 | 1071823774337 |
| 186 | 1171432692373 |
| 187 | 1280011042268 |
| 188 | 1398341745571 |
| 189 | 1527273599625 |
| 190 | 1667727404093 |
| 191 | 1820701100652 |
| 192 | 1987276856363 |
| 193 | 2168627105469 |
| 194 | 2366022741845 |
| 195 | 2580840212973 |
| 196 | 2814570987591 |
| 197 | 3068829878530 |
| 198 | 3345365983698 |
| 199 | 3646072432125 |
| 200 | 3972999029388 |
| 201 | 4328363658647 |
| 202 | 4714566886083 |
| 203 | 5134205287973 |
| 204 | 5590088317495 |
| 205 | 6085253859260 |
| 206 | 6622987708040 |
| 207 | 7206841706490 |
| 208 | 7840656226137 |
| 209 | 8528581302375 |
| 210 | 9275102575355 |
| 211 | 10085065885767 |
| 212 | 10963707205259 |
| 213 | 11916681236278 |
| 214 | 12950095925895 |
| 215 | 14070545699287 |
| 216 | 15285151248481 |
| 217 | 16601598107914 |
| 218 | 18028182516671 |
| 219 | 19573856161145 |
| 220 | 21248279009367 |
| 221 | 23061871173849 |
| 222 | 25025873760111 |
| 223 | 27152408925615 |
| 224 | 29454549941750 |
| 225 | 31946390696157 |
| 226 | 34643126322519 |
| 227 | 37561133582570 |
| 228 | 40718063627362 |
| 229 | 44132934884255 |
| 230 | 47826239745920 |
| 231 | 51820051838712 |
| 232 | 56138148670947 |
| 233 | 60806135438329 |
| 234 | 65851585970275 |
| 235 | 71304185514919 |
| 236 | 77195892663512 |
| 237 | 83561103925871 |
| 238 | 90436839668817 |
| 239 | 97862933703585 |
| 240 | 105882246722733 |
| 114540884553038 | |
| 242 | 123888443077259 |
| 243 | 133978259344888 |
| 244 | 144867692496445 |
| 245 | 156618412527946 |
| 246 | 169296722391554 |
| 247 | 182973889854026 |
| 248 | 197726516681672 |
| 249 | 213636919820625 |
| 250 | 230793554364681 |
| 251 | 249291451168559 |
| 252 | 269232701252579 |
| 253 | 290726957916112 |
| 254 | 313891991306665 |
| 255 | 338854264248680 |
| 256 | 365749566870782 |
| 257 | 394723676655357 |
| 258 | 425933084409356 |
| 259 | 459545750448675 |
| 260 | 495741934760846 |
| 261 | 534715062908609 |
| 262 | 576672674947168 |
| 263 | 621837416509615 |
| 264 | 670448123060170 |
| 265 | 722760953690372 |
| 266 | 779050629562167 |
| 267 | 839611730366814 |
| 268 | 904760108316360 |
| 269 | 974834369944625 |
| 270 | 1050197489931117 |
| 271 | 1131238503938606 |
| 272 | 1218374349844333 |
| 273 | 1312051800816215 |
| 274 | 1412749565173450 |
| 275 | 1520980492851175 |
| 276 | 1637293969337171 |
| 277 | 1762278433057269 |
| 278 | 1896564103591584 |
| 279 | 2040825852575075 |
| 280 | 2195786311682516 |
| 281 | 2362219145337711 |
| 282 | 2540952590045698 |
| 283 | 2732873183547535 |
| 284 | 2938929793929555 |
| 285 | 3160137867148997 |
| 286 | 3397584011986773 |
| 287 | 3652430836071053 |
| 288 | 3925922161489422 |
| 289 | 4219388528587095 |
| 290 | 4534253126900886 |
| 291 | 4872038056472084 |
| 292 | 5234371069753672 |
| 293 | 5622992691950605 |
| 294 | 6039763882095515 |
| 295 | 6486674127079088 |
| 296 | 6965850144195831 |
| 297 | 7479565078510584 |
| 298 | 8030248384943040 |
| 299 | 8620496275465025 |
| 300 | 9253082936723602 |
| 301 | 9930972392403501 |
| 302 | 10657331232548839 |
| 303 | 11435542077822104 |
| 304 | 12269218019229465 |
| 305 | 13162217895057704 |
| 306 | 14118662665280005 |
| 307 | 15142952738857194 |
| 308 | 16239786535829663 |
| 309 | 17414180133147295 |
| 310 | 18671488299600364 |
| 311 | 20017426762576945 |
| 312 | 21458096037352891 |
| 313 | 23000006655487337 |
| 314 | 24650106150830490 |
| 315 | 26415807633566326 |
| 316 | 28305020340996003 |
| 317 | 30326181989842964 |
| 318 | 32488293351466654 |
| 319 | 34800954869440830 |
| 320 | 37274405776748077 |
| 321 | 39919565526999991 |
| 322 | 42748078035954696 |
| 323 | 45772358543578028 |
| 324 | 49005643635237875 |
| 325 | 52462044228828641 |
| 326 | 56156602112874289 |
| 327 | 60105349839666544 |
| 328 | 64325374609114550 |
| 329 | 68834885946073850 |
| 330 | 73653287861850339 |
| 331 | 78801255302666615 |
| 332 | 84300815636225119 |
| 333 | 90175434980549623 |
| 334 | 96450110192202760 |
| 335 | 103151466321735325 |
| 336 | 110307860425292772 |
| 337 | 117949491546113972 |
| 338 | 126108517833796355 |
| 339 | 134819180623301520 |
| 340 | 144117936527873832 |
| 341 | 154043597379576030 |
| 342 | 164637479165761044د> |
| 343 | 175943559810422753 |
| 344 | 188008647052292980 |
| 345 | 200882556287683159 |
| 346 | 214618299743286299 |
| 347 | 229272286871217150 |
| 348 | 244904537455382406 |
| 349 | 261578907351144125 |
| 350 | 279363328483702152 |
| 351 | 298330063062758076 |
| 352 | 318555973788329084 |
| 353 | 340122810048577428 |
| 354 | 363117512048110005 |
| 355 | 387632532919029223 |
| 356 | 413766180933342362 |
| 357 | 441622981929358437 |
| 358 | 471314064268398780 |
| 359 | 502957566506000020 |
| 360 | 536679070310691121 |
| 361 | 572612058898037559 |
| 362 | 610898403751884101 |
| 363 | 651688879997206959 |
| 364 | 695143713458946040 |
| 365 | 741433159884081684 |
| 366 | 790738119649411319 |
| 367 | 843250788562528427 |
| 368 | 899175348396088349 |
| 369 | 958728697912338045 |
| 370 | 1022141228367345362 |
| 371 | 1089657644424399782 |
| 372 | 1161537834849962850 |
| 373 | 1238057794119125085 |
| 374 | 1319510599727473500 |
| 375 | 1406207446561484054 |
| 376 | 1498478743590581081 |
| 377 | 1596675274490756791 |
| 378 | 1701169427975813525 |
| 379 | 1812356499739472950 |
| 380 | 1930656072350465812 |
| 381 | 2056513475336633805 |
| 382 | 2190401332423765131 |
| 383 | 2332821198543892336 |
| 384 | 2484305294265418180 |
| 385 | 2645418340688763701 |
| 386 | 2816759503217942792 |
| 387 | 2998964447736452194 |
| 388 | 3192707518433532826 |
| 389 | 3398704041358160275 |
| 390 | 3617712763867604423 |
| 391 | 3850538434667429186 |
| 392 | 4098034535626594791 |
| 393 | 4361106170762284114 |
| 394 | 4640713124699623515 |
| 395 | 4937873096788191655 |
| 396 | 5253665124416975163 |
| 397 | 5589233202595404488 |
| 398 | 5945790114707874597 |
| 399 | 6324621482504294325 |
| 400 | 6727090051741041926 |
| 401 | 7154640222653942321 |
| 402 | 7608802843339879269 |
| 403 | 8091200276484465581 |
| 404 | 8603551759348655060 |
| 405 | 9147679068859117602 |
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
كما سئل في فيلم Mean Girls ، ما هو:
لنبدأ بالنظر إلى رسم بياني لـ n (محور x) وf(n) (محور y).
كما ترى، يقترب الحد من ∞ من اليسار و-∞ من اليمين. ولأنه لا ينعكس إلى نفس المكان من كلا الجانبين، فلا يوجد حد.
مع ذلك، لنُجِب على السؤال دون تمثيل بياني. تنص قاعدة لوبيتال على أنه إذا كانت نهاية f(x)/g(x) = 0/0، فإن lim f(x)/g(x) = lim f'(x)/g'(x). لذا، لنُحَل قيم f'(x) وg'(x).
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn
دعنا نستخدم قاعدة الضرب لحل sin 2 (n) d/dn
الخطيئة 2 (ن) د/دن = الخطيئة(ن) × الخطيئة(ن) د/دن =
الخطيئة (ن) × جتا (ن) + جتا (ن) × الخطيئة (ن) =
2sin(n)cos(n).
الآن، دعنا نحل f'(n) و g'(n) عند n = 0.
f'(0) = -1/(1-0) - cos(0) = -2.
g'(0) = 2sin(0)cos(0) = 0
إذًا، f'(0)/g'(0) = -2/0 = -∞. وبالتالي، فإن نهاية الدالة الأصلية غير موجودة.

أود أن أشيد بكتاب فيلم "فتيات لئيمات" على دقة حساباتهم. حتى الأفلام الرياضية الجادة، مثل "غود ويل هانتينغ"، غالبًا ما تُخفق في تطبيقها.
في الحلقة الرابعة من الموسم الثالث من مسلسل "شيلدون الصغير"، بعنوان "الهوبيت، الفيزياء، وكرة ذات سحاب" ، يسأل شيلدون نفسه عن عدد التركيبات الممكنة على بطاقة بنغو. ما هي الإجابة؟ وهل الصيغ المعروضة في المسلسل صحيحة؟
أولاً، سأستعرض عدد التباديل. هذا يعني أن الأرقام ليست مهمة فحسب، بل ترتيبها على البطاقة أيضاً. هناك معادلة (١٥، ٥) = ١٥!/(١٥-٥)! = ١٥*١٤*١٣*١٢*١١ = ٣٦٠،٣٦٠ تبديلاً محتملاً للأعمدة B وI وG وO. أما بالنسبة للعمود N، فعدد التباديل هو معادلة (١٤، ٤) = ١٥!/(١٥-٤)! = ١٥*١٤*١٣*١٢ = ٣٢،٧٦٠. وبالتالي، فإن العدد الإجمالي لتباديل بطاقات البنغو هو ٣٦٠،٣٦٠ ٤ × ٣٢،٧٦٠ = ٥٥٢٤٤٦٤٧٤٠٦١١٢٨٦٤٨٦٠١٦٠٠٠٠٠٠.
ثانيًا، سأستعرض عدد التباديل. هذا يعني أن الأرقام مهمة، وليس ترتيبها على البطاقة. هناك 3003 تباديل محتملة للأعمدة B وI وG وO، وهي: combin(15,5) = 15!/(5!*(15-5)!) = (15*14*13*12*11)/(1*2*3*4*5) = 3003 تباديل محتملة للأعمدة B وI وG وO. أما بالنسبة للعمود N، فعدد التباديل هو: combin(14,4) = 15!/(4!*(15-4)!) = (15*14*13*12)/(1*2*3*4) = 1365. وبالتالي، فإن إجمالي عدد تباديل بطاقات البنغو هو 3003 4 × 1365 = 111007923832370565.
في البرنامج، يتساءل شيلدون عن كيفية وجود بطاقات بنغو فريدة. بناءً على الصيغ الخاطئة لاحقًا، أفترض أنه يقصد التباديل. بمعنى آخر، بطاقتان بنفس الأرقام ولكن في مواقع مختلفة ستكونان فريدتين.
تُظهر الصورة أعلاه صيغة شيلدون للأعمدة B وI وG وO. في البداية، حصل على الصيغة الصحيحة عند 5! × combin(15,5). إلا أنه بسّطها بشكل خاطئ إلى 15!/(15!-5)!. كان من المفترض ألا تظهر علامة التعجب الثانية، بل 15!/(15-10)!. ثم عاد إلى الإجابة الصحيحة عند 360,360.

لدينا نفس المشكلة تمامًا مع العمود N. يجب أن تكون الصيغة 15!/(15-4)!، وليس 15!/(15!-4)!. علامة التعجب الثانية تُفسدها.
الشيء المثير للسخرية هو أنه في وقت لاحق من الحلقة، أصبح شيلدون مهووسًا بالأخطاء في التسلسل الزمني لسيد الخواتم، تمامًا كما أنا مهووس بهذا.

لدينا خزان ممتلئ سعة ١٠٠ لتر يحتوي على ماء و١٠ كجم من الملح. إذا أضفنا ١٠ لترات من الماء النقي كل دقيقة، مع تصريف ١٠ لترات من المحلول في نفس الوقت، فما كمية الملح المتبقية في الخزان بعد ٣٠ دقيقة؟
دعونا نبدأ بتعريف زوج من المتغيرات:
- س = كجم من الملح في الخزان
- t = دقائق منذ إلقاء الملح في الخزان
علمنا أن ١٠٪ من الملح يُصرف في الدقيقة. وبعبارة رياضية:
ds/dt = (-10/100) × s
دعونا نعيد ترتيب ذلك إلى:
ds = (-10/100) × s dt
-10/ثانية ds = dt
دمج كلا الجانبين:
(1) -10×ln(s) = t + c
الآن، لنوجد ثابت التكامل المهم. للقيام بذلك، نعلم أن s = 10 عندما t = 0. بتطبيق ذلك في الصيغة (1) أعلاه، نحصل على:
-10 × ln(10) = 0 + c
لذا c = -10×ln(10)
بوضع ذلك في المعادلة (1) نحصل على:
(2) -10×ln(s) = t -10×ln(10)
السؤال المطروح هو: ما كمية الملح الموجودة في الخزان عند t=30؟ حل s عند t=30:
-10×ln(s) = 30 -10×ln(10). ثم اقسم كلا الطرفين على -10...
ln(s) = -3 + ln(10)
س = exp(-3 + ln(10))
س = exp(-3) × exp(ln(10))
س = exp(-3) × 10
س = ~ 0.4979 كجم من الملح.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
بما أن الشكل الأكبر عبارة عن مربع، ما هي مساحة x؟
مفتاح حل مثل هذه المسائل يكمن في إعدادها. أنصح بمحاولة تلخيص المسألة إلى أقل عدد ممكن من المجهولات. في هذه الحالة، يمكننا التعبير عن المسافات المجهولة على المربع بثلاثة فقط، كما يلي:
التعامل مع المستطيلات أسهل من التعامل مع المثلثات. بمعرفة مساحة ثلاثة مثلثات، يمكننا مضاعفة حجمها ومساحاتها. هذا يعطينا:
- أ ب = 10
- التيار المتردد=16
- (ab)(ac)=14
دعونا نحلل (ab)(ac):
أ 2 - أ ب - أ ج + ب ج = 14
أ 2 - 10 - 16 + ب ج = 14
(1) أ 2 + ب ج = 40
دعونا نعبر عن b و c من حيث a، لتقليص هذا إلى متغير واحد:
ب = 10/أ
ج = 16/أ
استبدال تلك القيم لـ b و c في المعادلة (1):
أ 2 + (10/أ)*(16/أ) = 40
أ 2 + 160/أ 2 = 18
الآن، دعونا نتخلص من الرقم 2 في المقام عن طريق ضرب كل شيء في 2 .
أ 4 + 160 = 40*أ 2
أ 4 - 40*أ 2 + 160 = 0
دعونا نحدد متغيرًا جديدًا y = a 2
ص 2 - 18ص + 32 = 0
بعد ذلك، دعنا نحل المعادلة y باستخدام الصيغة التربيعية:
y = (40 +/- الجذر التربيعي (1600-640))/2
y = (40 +/- الجذر التربيعي (960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4*sqrt(15)
مساحة المربع بالكامل هي 2 ، وهي تساوي y. بناءً على المعادلة السابقة، إذا كانت قيمة +/- سالبة، فإن y = apx 4.5081، وهو خطأ واضح، لأننا نعلم أن المساحة تساوي 20 على الأقل، حتى مع x. لذا، يجب أن تكون مساحة المربع 20 + 4*sqrt(15).
مساحة المثلثات الثلاثة المعطاة هي ٥ + ٧ + ٨ = ٢٠. بطرح هذه المساحة من المساحة الكلية للمربع، نحصل على مساحة x: ٢٠ + ٤*الجذر التربيعي (١٥) - ٢٠ = ٤*الجذر التربيعي (١٥) = تقريبًا ١٥٫٤٩١٩.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .

لاحظ قميصي في هذه الصورة. أثنى عليه أمين الصندوق في دار السينما عندما ذهبت لمشاهدة فيلم Uncut Gems . شكرتها بإزعاجها بهذه المسألة، باستخدام مثلثات المناطق ٢ و٣ و٤ فقط. بعد الفيلم، تحققت منها، ولم تتمكن من حلها بعد، ولكن يبدو أنها تحاول. لذلك كتبت لها الحل التالي في حانة Suncoast. بدت ممتنة له بالفعل. أعتقد أن هذه الفتاة ستصل إلى آفاق جديدة في حياتها.
هناك لوحة رمي سهام مربعة أبعادها ١ × ١. رُمي سهم عليها بحيث يسقط في أي مكان باحتمالية متساوية. لنفترض أن إحداثيات نقطة سقوطها هي (س، ص)، حيث يكون كلٌّ من س وص موزعين بالتساوي وبشكل مستقل من ٠ إلى ١.
ليكن z = تقريب (س/ص). بمعنى آخر، z = س/ص، مُقرَّبًا لأقرب عدد صحيح. ما احتمال أن يكون z زوجيًا؟
سيكون من المفيد جدًا معرفة السلسلة اللانهائية في التلميح التالي.
[المفسد=تلميح]تنص صيغة لايبنتز لـ π على:
1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
[/spoiler]للحصول على الإجابة فقط انقر على الزر التالي.
[سبويلر=الإجابة](5 - π)/4 = apx. 0.464601836602552. [/spoiler]انقر على الزر أدناه للحصول على الحل.
إذا كانت x/y < 0.5، فسيتم تقريب النسبة إلى n، أي إلى 0، أو إلى عدد زوجي. أي نقطة على لوحة السهام على يسار الخط المكوّن من (0،0) و(0.5) سيتم تقريبها إلى 0. هذه المساحة مثلث قائم الزاوية طول ضلعه 1 و1/2. تذكر أن مساحة المثلث هي (1/2) × القاعدة × الارتفاع. وبالتالي، فإن مساحة هذه النقاط عند تقريبها إلى 0 هي (1/2) × (1/2) = 1/4.
المنطقة التالية على الرسم البياني التي سيتم تقريبها إلى العدد الزوجي التالي، 2، هي عندما يكون 1.5 < x/y < 2.5. ستكون هذه المنطقة مثلثًا قاعدته 2/3 - 2/5 وارتفاعه 1. لاحظ أن هذه هي معكوسات حدود x/y، لأن x يساوي 1، لذا نحتاج إلى عكس y. إذن، المنطقة التي سيتم تقريبها إلى 2 هي (1/2)*(2/3 - 2/5).
المنطقة التالية على الرسم البياني التي سيتم تقريبها إلى العدد الزوجي التالي، 4، هي عندما يكون 3.5 < x/y < 4.5. ستكون هذه المنطقة مثلثًا قاعدته 2/7 - 2/9 وارتفاعه 1. لذا، فإن المنطقة التي سيتم تقريبها إلى 2 هي (1/2)*(2/7 - 2/9).
المنطقة التالية على الرسم البياني التي سيتم تقريبها إلى العدد الزوجي التالي، 6، هي عندما يكون 5.5 < x/y < 6.5. ستكون هذه المنطقة مثلثًا قاعدته 2/11 - 2/13 وارتفاعه 1. لذا، فإن المنطقة التي سيتم تقريبها إلى 2 هي (1/2)*(2/11 - 2/13).
هل بدأت ترى نمطًا؟ إنه كالتالي:
1/4 + 1/2*(2/3 - 2/5 + 2/7 - 2/9 + 2/11 - 2/13 + ... ) =
1/4 + (1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
دعنا ننقل -1 داخل هذه الأقواس.
5/4 + (-1 + 1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
5/4 - (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 + ... ) =
بعد ذلك، تذكر تلميحنا أعلاه:
1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11
العودة إلى السؤال المطروح ...
5/4 - π/4 =
(5 - π) / 4 = أبكس. 0.464601836602552.
من المثير للاهتمام كيف يستمر ظهور π و e في كل مكان في الرياضيات.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ليكن 9x + 12x = 16x
ما هو x؟
انقر على الزر أدناه للحصول على الإجابة.
انقر على الزر أدناه للحصول على الحل.
9x + 12x = 16x =
اقسم كلا الطرفين على 9 ×
1 + (12/9) x = (16/9) x
1 + (4/3) x = ((4/3) x ) 2
(1) ليكن u = (4/3) x
1 + u = u 2
بالصيغة التربيعية...
u = (1+sqrt(5)) / 2 (النسبة الذهبية)
وبإعادة ذلك إلى المعادلة (1):
(4/3) x = (1+sqrt(5)) / 2
خذ السجل لكلا الجانبين:
x ln(4/3) = ln[(1+sqrt(5)) / 2]
x = ln[(1+sqrt(5)) / 2] / ln(4/3)
x = [ln(1+sqrt(5) - ln(2)] / [ln(4) - ln(3)] = تقريبًا 1.67272093446233.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
الإقرار: لقد حصلت على اختلاف لهذه المشكلة من Presh Talwalkar من Mind Your Decisions .
يزرع مزارع خمس بذور تفاح. كل يوم، لكل بذرة فرصة إنبات ثلثها. ما هو متوسط الوقت اللازم لإنبات الأشجار الخمس؟
يزرع مزارع خمس بذور تفاح. كل يوم، لكل بذرة فرصة إنبات ثلثها. ما هو متوسط الوقت اللازم لإنبات الأشجار الخمس؟
لنحسب ذلك بطريقة عكسية. إذا بقيت بذرة واحدة لم تنبت، فسيستغرق إنباتها في المتوسط يومًا واحدًا/ب، حيث p هو احتمال إنباتها في أي يوم. وبما أن p = 1/3، فسيستغرق إنباتها في المتوسط 3 أيام. لنسمِّ ذلك t = 1 = 3.
ماذا لو تبقى بذرتان؟ احتمال ap 2 = 1/9 أن تنبت كلتاهما في اليوم التالي وننتهي من ذلك. احتمال أن تنبت إحداهما في اليوم التالي هو 2×p×q، حيث q هو احتمال عدم إنباتها. وبالتالي، فإن احتمال إنبات بذرة واحدة هو 2×(1/3)(2/3) = 4/9. احتمال عدم إنبات أيٍّ من البذرتين هو q 2 = (2/3) 2 = 4/9. لنسمِّ عدد الأيام المتوقع لوجود بذرتين t 2 .
t 2 = 1 + (4/9)×t 1 + (4/9)t 2
t 2 = (1 - (4/9)) = 1 + (4/9)×t 1
t 2 = (1 + (4/9)×3) / (1 - (4/9))
t 2 = (21/9) / (5/9)
t 2 = (21/9) × (9/5) = 21/5 = 4.2
ماذا لو تبقى ثلاث بذور؟ احتمال أن تنبت جميعها في اليوم التالي هو ap 3 = 1/27. احتمال أن تنبت واحدة في اليوم التالي هو 3×p×q 2 = 3×(1/3)(2/3) 2 = 12/27. احتمال أن تنبت اثنتان في اليوم التالي هو 3×p 2 ×q = 3×(1/3) 2 ×(2/3) = 6/27. احتمال عدم إنبات أي بذور هو q 3 = (2/3) 3 = 8/27. لنسمِّ العدد المتوقع للأيام التي تحتوي على ثلاث بذور t 3 .
t 3 = 1 + (6/27)t 1 + (12/27)×t 2 + (8/27)×t 3
t 3 = 1 + (6/27)×3 + (12/27)×4.2 + (8/27)×t 3
ت 3 × (1 - 8/27) = (1 + 18/27 + 28/15)
t 3 = (1 + 18/27 + 28/15) / (1 - 8/27) = 477/95 = تقريبًا 5.02105263
ماذا لو تبقى أربع بذور؟ هناك احتمال ap 4 = 1/81 أن تنبت جميع البذور الأربع في اليوم التالي وننتهي. احتمال أن تنبت واحدة في اليوم التالي هو 4×p×q 3 = 4×(1/3)(2/3) 3 = 32/81. احتمال أن تنبت اثنتان في اليوم التالي هو combin(4,2)×p 2 ×q 2 = 6×(1/3) 2 ×(2/3) 2 = 24/81. احتمال أن تنبت ثلاث بذور في اليوم التالي هو combin(4,3)×p 3 ×q = 4×(1/3) 3 ×(2/3) = 8/81. احتمال عدم إنبات أي بذور هو q 4 = (2/3) 4 = 16/81. لنسمي العدد المتوقع للأيام التي تحتوي على ثلاث بذور t 4 .
t 4 = 1 + (8/81)×t 1 + (24/81)×t 2 + (32/81)×t 3 + (16/81)×t 4
t 4 = 1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263 + (16/81)×t 4
t 4 = (1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263) / (1 - (16/81))
t 4 = تقريبًا 5.638056680161943319838056680.
ماذا لو تبقى خمس بذور؟ احتمال ap 5 = 1/243 أن تنبت جميع البذور الخمس في اليوم التالي وننتهي. احتمال أن تنبت واحدة في اليوم التالي هو 5×p×q 4 = 5×(1/3)(2/3) 4 = 80/243. احتمال أن تنبت اثنتان في اليوم التالي هو combin(5,2)×p 2 ×q 3 = 10×(1/3) 2 ×(2/3) 3 = 80/243. احتمال أن تنبت ثلاث بذور في اليوم التالي هو combin(5,3)×p 3 ×q = 10×(1/3) 3 ×(2/3) 2 = 40/243. احتمال أن تنبت أربع بذور في اليوم التالي هو combin(5,4)×p 4 ×q = 5×(1/3) 4 ×(2/3) = 10/243. احتمال عدم إنبات أي بذور هو q 5 = (2/3) 5 = 32/243. لنسمِّ عدد الأيام المتوقع لظهور ثلاث بذور t 5 .
t 5 = 1 + (10/243)×t 1 + (40/243)×t 2 + (80/81)×t 3 + (80/243)×t 4 + (32/243)×t 5
t 5 = (1 + (10/243)×t 1 + (40/243)×t 2 + (80/81)×t 3 + (80/243)×t 4 ) / (1 - (32/243))
t 5 = (1 + (10/243)×3 + (40/243)×4.2 + (80/243)×(477/95) + (80/243)×5.63805668) / (1 - (32/243))
t 5 = تقريبًا 6.131415853.
تم تعديل هذه المشكلة من مشكلة مماثلة كتبها بريش تالوالكار في Mind Your Decisions .
لدي سؤال مكون من جزأين.
بالنسبة للجزء الأول، معطى:- x + y + z = 1
- x^2 + y^2 + z^2 = 4
- x^3 + y^3 + z^3 = 9
ما هو x^4 + y^4 + z^4 ؟
بالنسبة للجزء الثاني، ما هو الجواب للحالة العامة عندما:
- x + y + z = أ
- x^2 + y^2 + z^2 = b
- x^3 + y^3 + z^3 = c
السؤال 1: 97/6 = تقريبًا 16.166666
السؤال 2: أ 4/6 + (4/3) أ ج - أ 2 ب + ب 2/2
لمشاهدة حلي (PDF)
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يمكن لميكروب، لنسمِّه كوفيد-20، أن يُفرخ ميكروبًا جديدًا في أي وقت. واحتمالية ظهور ميكروب معين في أي وقت، من ميكروب أبوي محدد، ثابتة دائمًا، بغض النظر عن الوقت المنقضي منذ آخر ظهور. ويبلغ متوسط المدة بين ظهور الميكروب نفسه يومًا واحدًا. رياضيًا، يتبع الوقت المتوقع بين ظهور الميكروب نفسه توزيعًا أُسيًا بمتوسط يوم واحد.
بمجرد دخول الميكروب إلى رئتيك، ما هو عدد الميكروبات المتوقع أن يكون لديك بعد سبعة أيام؟
انقر على الزر أدناه للحصول على الإجابة.
انقر على الزر أدناه للحصول على الحل.
سيتطلب هذا الحل معادلة تفاضلية عادية. إذا لم تكن قد وصلت إلى هذه المرحلة بعد في دراسة الرياضيات، فلن تفهمه.
يترك:
م = عدد ميكروبات كوفيد-20
t = الوقت، بالأيام
بما أن كل ميكروب يُنتج ميكروبًا جديدًا بمعدل مرة واحدة يوميًا، فإن متوسط عدد الميكروبات (m) سيُنتج (m) ميكروبًا جديدًا يوميًا. بمعنى آخر، يُمكن كتابة معدل الزيادة في عدد الميكروبات (m) في أي وقت (t) على النحو التالي:
د م/د ت = م.
أنا لست متأكدًا من الطريقة الصحيحة للتعبير عن هذا، ولكن افصل dt إلى الجانب الأيمن:
د م = م د ت.
اقسم كلا الطرفين على م:
1/م دسم = 1 د ت.
دمج كلا الجانبين:
ln(m) = t + C، حيث C هو ثابت التكامل.
نعلم أنه في اللحظة ٠ يوجد ميكروب واحد. بمعنى آخر، عندما تكون t = ٠، تكون m = ١. يمكننا وضع هذه القيم في المعادلة أعلاه لإيجاد قيمة C:
ln(1) = 0 + C
0 = 0 + ج
ج = 0.
لدينا الآن ln(m) = t.
خذ exp() لكلا الجانبين:
م = هـ ت
لذا، في الوقت t=7، سيكون هناك e7 = تقريبًا 1096.6332 ميكروبًا.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في صالون غربي قديم، تطور جدال حول لعبة الورق إلى قيام جميع رعاة البقر في المنطقة بسحب بنادقهم وإطلاق النار على بعضهم البعض.
عندما انقشع الدخان أخيرًا، كان 90% من رعاة البقر قد أصيبوا بطلقات نارية في أرجلهم، و85% في أذرعهم، و80% في أمعائهم، و75% في رؤوسهم. والمثير للدهشة أن رعاة البقر الذين أصيبوا بالأنواع الأربعة من الإصابات فقط هم من لقوا حتفهم في تبادل إطلاق النار العنيف.
ما هي أصغر نسبة ممكنة من رعاة البقر الذين انتهى بهم الأمر إلى الدفن؟
أولاً، قم بإطلاق النار على 90% من رعاة البقر في الساق.
بعد ذلك، أطلق النار على الـ ١٠٪ المتبقية في الذراع. لديك ٧٥٪ إضافية لإطلاقها في الذراع، لذا أطلقها من تلك التي أصابتها في الساق.
إذن، نحن الآن عند:
الساق فقط 15% (90% - 75%)
الذراع فقط 10%
كلاهما 75%
لا 0%
المجموع الكلي للساق: 90%
إجمالي الذراع: 85%
الآن، لننتقل إلى إصابات الأمعاء (80%). استهدف الـ 25% من المصابين بإصابة واحدة فقط في الأمعاء. لدينا 80% - 25% = 55% زيادة في عدد الأشخاص الذين يجب استهدافهم. سنأخذ هذه الـ 55% من مجموعة المصابين بكلتا الإصابتين. الآن وصلنا إلى:
الساق والأمعاء 15٪
الذراع والأمعاء 10%
الساق والذراع 20% (75% - 55%)
الثلاثة 55%
إصابة واحدة 0%
صفر إصابات 0%
أخيرًا، لنأخذ نسبة 75% من الإصابات في الرأس. أولًا، نستهدف نسبة 45% مع إصابتين فقط. يتبقى لدينا 30% إضافية، لذا نستهدف نسبة 55% مع الإصابات الثلاث. هذا يتبقى:
الرأس والساق والأمعاء 15%
الرأس والذراع والأمعاء 10%
الرأس والساق والذراع 20%
الساق والذراع والأمعاء: 25% (55% - 30%)
جميع الأربعة 30%
صفر إصابات 0%
إصابة واحدة 0%
إصابتان 0%
لنفترض أن لدينا ٢٠ راعي بقر. اخترنا هذا الرقم لأن جميع الاحتمالات قابلة للقسمة بالتساوي على ٥٪، و٥٪ من ٢٠ تساوي ١.
رتبهم في صف واحد. ثم، ابدأ باليسار، واضرب 90% منهم، أي 18، في الساق. ثم ارسم مخططًا برقم راعي البقر على طول الصف العلوي وإجمالي إصابات كل منهم على طول العمود الأيسر، كما يلي.
| إصابة | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ||
| 2 | ||||||||||||||||||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| المجموع | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
بعد ذلك، عليك تسجيل 85%، أو 17 نقطة في الذراع. ابدأ بلاعبَي رعاة البقر اللذين لم يُصابا في ساقيهما. لديك 15 نقطة أخرى متبقية. عُد إلى لاعب رعاة البقر على اليسار وتحرك لأسفل الصف، مُسجلاً 15 نقطة مُصابة بالفعل في ساقيهما. يجب أن تبدو بطاقة الإصابة الخاصة بك كما يلي:
| إصابة | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | أ | أ |
| 2 | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | |||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| المجموع | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 |
بعد ذلك، عليك تسجيل 80%، أو 16 نقطة في منطقة البطن. ابدأ بخمسة رعاة بقر مصابين بإصابة واحدة فقط. لديك 11 نقطة أخرى. ارجع إلى راعي البقر على اليسار وتحرك للأسفل، مسجلاً 11 نقطة إجمالية مصابة مرتين. يجب أن تبدو بطاقة إصابتك كما يلي:
| إصابة | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | أ | أ |
| 2 | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | ج | ج | ج | ج | ج |
| 3 | ج | ج | ج | ج | ج | ج | ج | ج | ج | ج | ج | |||||||||
| 4 | ||||||||||||||||||||
| المجموع | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
بعد ذلك، عليك تسجيل 75%، أو 15 نقطة في الرأس. ابدأ بتسع رعاة بقر مصابين مرتين فقط. لديك 6 نقاط أخرى. ارجع إلى راعي البقر على اليسار وتحرك لأسفل الصف، مسجلاً ما مجموعه 6 نقاط مصابة بالفعل ثلاث مرات. يجب أن تبدو بطاقة إصابتك كما يلي:
| إصابة | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | ل | أ | أ |
| 2 | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | أ | ج | ج | ج | ج | ج |
| 3 | ج | ج | ج | ج | ج | ج | ج | ج | ج | ج | ج | ح | ح | ح | ح | ح | ح | ح | ح | ح |
| 4 | ح | ح | ح | ح | ح | ح | ||||||||||||||
| المجموع | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
كما ترون، أُصيب ستة رعاة بقر أربع مرات، بينما أُصيب أربعة عشر رعاة بقر ثلاث مرات. وبالتالي، فإن النسبة القصوى التي يمكن أن تُصاب بثلاث إصابات فقط هي 14/20 = 70%.
بالنسبة للحالة العامة، إذا كانت الاحتمالات الأربعة هي أ، ب، ج، د، فإن النسبة القصوى التي يمكن أن تعيش هي 1-(أ+ب+ج+د)، طالما أن أ+ب+ج+د >=3 و أ+ب+ج+د <=4.
أود أن أشكر وأشكر عضو منتدى Wizard of Vegas CharliePatrick على هذا الحل.
تم طرح هذا السؤال ومناقشته في منتدياتي، بدءًا من هذه التدوينة .
يستطيع الضفدع القفز قدمًا أو قدمين. يقفز الضفدع مسافة عشرة أقدام بالضبط على عدة قفزات، دائمًا للأمام. بكم طريقة مختلفة يمكن القيام بذلك، مع مراعاة مسافة القفزة وترتيبها؟
- إذا كان على الضفدع أن يقفز بقدم واحدة فقط، فمن البديهي أن هناك طريقة واحدة فقط. تذكر، لا يمكن للضفدع أن يتجاوز هدفه.
- إذا كان الضفدع يحتاج إلى القفز قدمين، فهناك طريقتان للقيام بذلك - (1) قدم واحدة وقدم واحدة، أو (2) قدمين.
إذا احتاج الضفدع للقفز مسافة ثلاثة أقدام، فيمكنه أن يكون على بُعد قدم واحدة أو قدمين قبل القفزة الأخيرة. هناك طريقة واحدة ليكون على بُعد قدمين، كما هو موضح في الخطوة 1، وطريقتان ليكون على بُعد قدم واحدة، كما هو موضح في الخطوة 2. وبالتالي، هناك ثلاث طرق للقفز على بُعد ثلاثة أقدام. ويمكن التحقق من ذلك بسهولة أيضًا من خلال: (1) 1+1+1، (2) 1+2، (3) 2+1.
إذا احتاج الضفدع للقفز مسافة أربعة أقدام، فيمكنه أن يكون على بُعد قدمين أو ثلاثة أقدام قبل القفزة الأخيرة. هناك طريقتان ليكون على بُعد قدمين، كما هو موضح في الخطوة ٢، وثلاث طرق ليكون على بُعد قدم واحدة، كما هو موضح في الخطوة ٣. وبالتالي، هناك خمس طرق للقفز على بُعد أربعة أقدام. ويمكن التحقق من ذلك بسهولة أيضًا على النحو التالي: (١) ١+١+١+١، (٢) ١+١+٢، (٣) ١+٢+١، (٤) ٢+١+١، (٥) ٢+٢.
إذا احتاج الضفدع للقفز مسافة 5 أقدام، فيمكنه أن يكون على بُعد 3 أقدام أو 4 أقدام قبل القفزة الأخيرة. هناك 3 طرق ليكون على بُعد قدمين، كما هو موضح في الخطوة 3، و5 طرق ليكون على بُعد قدم واحدة، كما هو موضح في الخطوة 4. وبالتالي، هناك 3 + 5 = 8 طرق للقفز على بُعد 5 أقدام. ويمكن التحقق من ذلك بسهولة أيضًا على النحو التالي: (1) 1 + 1 + 1 + 1 + 1 + 1، (2) 1 + 1 + 1 + 2، (3) 1 + 1 + 2 + 1، (4) 1 + 2 + 1 + 1، (5) 2 + 1 + 1 + 1، (6) 2 + 2 + 1، (7) 2 + 1 + 2، (8) 1 + 2 + 2.
هل بدأتَ تلاحظ نمطًا؟ إنه متوالية فيبوناتشي. باتباع نفس المنطق، هناك 89 طريقة يستطيع بها الضفدع القفز مسافة عشرة أقدام بالضبط.باستخدام العملات المعدنية الأمريكية القياسية من فئة 1، 5، 10، 25، 50 سنتًا و1 دولار، كم عدد الطرق التي يمكن بها تغيير المبلغ إلى 1 دولار؟
دع a(x) = عدد الطرق لتكوين x سنتات، باستخدام البنسات والنيكل فقط، حيث x هو عدد قابل للقسمة على 5.
أ(س) = 1+(س/5)
بعبارة أخرى، عدد الطرق هو عدد النيكلات المحتملة في التغيير، والتي تتراوح من 0 إلى x/5.
دع b(x) = عدد الطرق لتكوين x سنتات، باستخدام البنسات والنيكل والدايمات فقط، حيث x هو عدد قابل للقسمة على 5.
ب(0)=1
ب(5)=2
b(x) = a(x) + b(x-10)، حيث x>=10.
باللغة الإنجليزية البسيطة، عدد الطرق لتكوين x سنتات، هو مجموع (1) b(x-10) = عدد الطرق لتكوين x-10 سنتات عن طريق إضافة عشرة سنتات إلى كل طريقة و(2) a(x) = عدد الطرق التي لا تستخدم عشرة سنتات.
دع c(x) = عدد الطرق لتكوين x سنتات، باستخدام البنسات، والنيكل، والدايم، والربع دولار فقط حيث x قابل للقسمة على 25.
ج(0) = 1
c(x) = b(x) + c(x-25)، حيث x>=25.
باللغة الإنجليزية البسيطة، عدد الطرق لتكوين x سنتات، هو مجموع (1) c(x-25) = عدد الطرق لتكوين x-25 سنتًا عن طريق إضافة ربع دولار إلى كل طريقة و(2) b(x) = عدد الطرق التي لا تستخدم فيها أي أرباع دولار.
دع d(x) = عدد الطرق لتكوين x سنتات، باستخدام البنسات، والنيكل، والدايم، والربع دولار، ونصف الدولار فقط حيث أن x قابل للقسمة على 50.
د(0) = 1
d(x) = c(x) + d(x-50)، حيث x>=50.
باللغة الإنجليزية البسيطة، عدد الطرق لكسب x سنتات، هو مجموع (1) d(x-50) = عدد الطرق لكسب x-50 سنتًا عن طريق إضافة نصف دولار إلى كل طريقة و(2) c(x) = عدد الطرق دون استخدام نصف دولار.
فيما يلي جدول يوضح هذه القيم لـ x = 5 إلى 100.
طرق إحداث التغيير
| س | الفأس) | ب(س) | ج(س) | د(س) |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | |
| 5 | 2 | 2 | 0 | |
| 10 | 3 | 4 | 0 | |
| 15 | 4 | 6 | 0 | |
| 20 | 5 | 9 | 0 | |
| 25 | 6 | 12 | 13 | |
| 30 | 7 | 16 | 0 | |
| 35 | 8 | 20 | 0 | |
| 40 | 9 | 25 | 0 | |
| 45 | 10 | 30 | 0 | |
| 50 | 11 | 36 | 49 | 50 |
| 55 | 12 | 42 | 0 | |
| 60 | 13 | 49 | 0 | |
| 65 | 14 | 56 | 0 | |
| 70 | 15 | 64 | 0 | |
| 75 | 16 | 72 | 121 | |
| 80 | 17 | 81 | 0 | |
| 85 | 18 | 90 | 0 | |
| 90 | 19 | 100 | 0 | |
| 95 | 20 | 110 | 0 | |
| 100 | 21 | 121 | 242 | 292 |
وأخيرًا، أضف واحدًا لعملة الدولار الواحد، والإجابة هي 292 + 1 = 293.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
هناك عدد لا نهائي من المصابيح الكهربائية، جميعها مطفأة. الفترة الزمنية بين تشغيل المصابيح الكهربائية لها توزيع أُسي* بمتوسط يوم واحد. بمجرد تشغيل المصباح الكهربائي، يتبع عمره الافتراضي أيضًا توزيعًا أُسيًا بمتوسط يوم واحد.
ما هو متوسط الوقت حتى يحترق المصباح الأول؟
*: للأحداث العشوائية التي تتبع التوزيع الأسّي خاصية عدم التذكر، حيث لا يُؤخذ الماضي في الاعتبار. بمعنى آخر، لا يتأخر حدث واحد أبدًا، واحتمال وقوعه ثابت دائمًا.
في المتوسط، سوف يستغرق الأمر يومًا واحدًا حتى يتم تشغيل المصباح الأول.
من هناك، سيستغرق الأمر نصف يوم، في المتوسط، حتى الحدث المهم التالي، سواءً أكان تشغيل مصباح جديد أم احتراق المصباح الأول. نضيف نصف يوم إلى مدة الانتظار حتى ذلك الحدث. إذن، لدينا الآن ١ + (١/٢) = ١.٥ يوم.
هناك احتمال بنسبة نصف أن يكون الحدث الثاني هو إضاءة مصباح ثانٍ. في هذه الحالة، هناك وقت انتظار قدره ثلث يوم حتى الحدث المهم التالي (إما احتراق أحد المصباحين الأولين أو إضاءة مصباح جديد). لذا، أضف حاصل ضرب النصف (احتمال الوصول إلى هذه المرحلة) في الثلث، الذي يساوي سدسًا، إلى وقت الانتظار. إذن، لسنا عند 1.5 + سدس = 5/3 = 1.66667 يومًا.
هناك احتمال (1/2)*(1/3) = 1/6 أن يكون الحدث المهم الثالث هو إضاءة مصباح ثالث. في هذه الحالة، هناك فترة انتظار قدرها ربع يوم حتى الحدث المهم التالي (إما احتراق أحد المصابيح الثلاثة الأولى أو إضاءة مصباح جديد). لذا، أضف حاصل ضرب 1/6 (احتمال الوصول إلى هذه المرحلة) في 1/4، الذي يساوي 1/24، إلى فترة الانتظار. إذن، لسنا عند 5/3 + 1/24 = 41/24 = 1.7083 يومًا.
باتباع هذا النمط، تكون الإجابة هي (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
يجب أن يكون من المعروف أن e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
الفرق الوحيد هو أن إجابتنا تفتقر إلى عامل ١/٠!. وبالتالي، فإن الإجابة هي e - ١/٠! = e - ١ = تقريبًا ١٫٧١٨٢٨١٨...
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
أ، ب، ج، د كلها أعداد صحيحة موجبة مختلفة.
أ < ب < ج < د
أوجد أكبر D بحيث
1/أ + 1/ب + 1/ج + 1/د = 1
الإجابة هي 42. أ، ب، ج هي 2، 3، و 7.
1/2 + 1/3 + 1/7 + 1/42 = 1.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
بعد مشاهدة برنامج "مناورة الملكة" ، لاحظتُ أن جميع مبارياته لم تنتهِ بالتعادل. كنتُ أعتقد أن مباريات الشطرنج في المستويات العليا تشهد الكثير من التعادل. بالنسبة لمستوى الأستاذ الكبير، ما نسبة المباريات التي تنتهي بالتعادل؟
وفقًا لمقال "هل ازداد عدد التعادلات في الشطرنج؟" على موقع ChessBase.com، ذكر الكاتب تشيو تشو أنه في 78,468 مباراة مُصنّفة بين لاعبين بتقييم 2600 نقطة أو أكثر (يتطلب الأمر 2500 نقطة ليصبح المرء أستاذًا كبيرًا)، كانت النتائج التالية:
- فوز الأسود: 18.0%
- يفوز الأبيض: 28.9%
- التعادل: 53.1%
هناك لوح خشبيّ بمقاس ٥×٥ وثلاثة أوتاد. ما احتمال أن تُشكّل ثلاثة أوتاد موضوعة عشوائيًا مثلثًا؟
أولاً، هناك combin(25,3) = 2,300 تركيبة ممكنة للأوتاد.
كم من هذه التركيبات تُشكّل مثلثًا؟ لنستخدم هذه اللوحة لمساعدتك:
أولاً، هناك خمسة صفوف وخمسة أعمدة وقطران. لكل منها، هناك 10 طرق لوضع الأوتاد في خط واحد. إذن، لدينا 12 × 10 = 120 طريقة.
ثانيًا، هناك أربع طرق لربط المربع المركزي لصف/عمود بمربع مركزي لصف/عمود مجاور. بعبارة أخرى، هذه هي المواضع الثلاثة:
- أ3، ب4، ج5
- C5، D4، E3
- هـ3، د2، ج1
- ج1، ب2، أ3
إذن، نحن الآن عند 120 + 4 = 124
ثالثًا، هناك أربعة خطوط قطرية مختلفة تمثل أربع مسافات:
- أ2، ب3، ج4، د5
- ب5، ج4، د3، هـ2
- هـ4، د3، ج2، ب1
- د1، ج2، ب3، أ4
لكلٍّ منها، هناك 4 طرق لوضع ثلاثة أوتاد. هذا يعني أن 4 × 4 = 16.
نحن الآن عند 124+16 = 140
رابعًا، لننظر إلى طريقة حركة الأحصنة في الشطرنج، على شكل حرف L 2×1. لكل زاوية طريقتان لحركة الحصان. في كل منهما، يمكن للحصان أن يتحرك مجددًا على نفس الخط الذي شكله في الحركة الأولى. إذن، 4×2 = 8 إضافية:
- أ1، ج2، هـ3 أ1، ب3، ج5
- أ5، ب3، ج1
- أ5، ج4، هـ3
- E5، C4، A3
- هـ5، د3، ج1
- هـ1، د3، ج5
- هـ1، ج2، أ3
هناك أيضًا أربعة خطوط فارس تمر عبر المركز:
- أ2، ج3، هـ4
- A4، C3، E2
- ب5، ج3، د1
- د5، ج3، ب1
بإضافة خطوط الفرسان الـ 12، نحصل على 140 + 12 = 152
إذا كان هناك 2300 تركيبة إجمالية و152 خطًا شكليًا، فإن 2300 - 152 = 2148 لا تشكل خطوطًا وبالتالي تشكل مثلثات.
وبالتالي، فإن إجابتنا هي 2,148/2,300 = 93.39%.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لقد تم إعطاؤك:
- هناك طائرة على بعد ثمانية أميال مباشرة فوق صاروخ أرض-جو، والذي يتم إطلاقه في تلك اللحظة.
- في جميع الأوقات، تسير الطائرة في اتجاه مستقيم.
- تتحرك الطائرة بسرعة 600 ميل في الساعة.
- يسافر الصاروخ بسرعة 2000 ميل في الساعة.
- يتحرك الصاروخ دائمًا بزاوية تواجه الطائرة مباشرة.
أسئلة:
- ما هي المسافة التي ستقطعها الطائرة قبل أن يضربها الصاروخ؟
- كم من الوقت سيستغرق الصاروخ حتى يضرب الطائرة؟
- ما هو طول مسار طيران الصاروخ؟
- ما هي المسافة التي ستقطعها الطائرة قبل أن يصيبها الصاروخ؟ = 240/91 ميلًا
- كم من الوقت سيستغرق الصاروخ لضرب الطائرة؟ = 2/455 ساعة
- ما هي المسافة التي سيقطعها الصاروخ؟ = 800/91 ميلًا
وهنا الحل الخاص بي (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يفترض:
- 90% من الجمهور يرتدون الأقنعة.
- احتمالية الإصابة بفيروس كورونا هي 1% لمن يرتدون الكمامات و3% لمن لا يرتدونها.
تم اختيار شخص عشوائيًا مصابًا بفيروس كورونا. ما احتمال أن يكون مرتديًا للكمامة؟
هذا هو سؤال الاحتمالات الشرطية البايزية الكلاسيكي.
الإجابة هي الاحتمالية (شخص يرتدي قناعًا ويعاني من فيروس كورونا) / الاحتمالية (شخص مصاب بفيروس كورونا) =
(0.9*0.01) / (0.9*0.01 + 0.1*0.03) = 75%.
هناك نملة في منتصف مربع. تبعد ١٧ بوصة عن الزاوية العلوية اليسرى، و٢٠ بوصة عن الزاوية العلوية اليمنى، و١٣ بوصة عن الزاوية السفلية اليمنى.
ما هو حجم المربع؟
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
[spoiler=إجابة]369 بوصة مربعة.
أولاً، قم بتدوير المثلث ABE بمقدار 90 درجة لتشكيل مثلث جديد BDF.
بما أن المثلث مُدار بزاوية ٩٠ درجة، فإن الزاوية EBF = ٩٠، حسب التعريف. ووفقًا لصيغة فيثاغورس، EF = ٢٠ × الجذر التربيعي (٢).
بموجب قانون جيب التمام: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*الجذر التربيعي(2)*جيب التمام(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
تذكر، sin^2(x) + cos^2(x) = 1. دعنا نستخدم ذلك لحل sin(DEF).
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
بعد ذلك، ضع في اعتبارك زاوية BED.
زاوية BED = زاوية BEF + زاوية FED.
نعلم أن الزاوية EBF تساوي 90 درجة، وهي مثلث متساوي الساقين. هذا يجعل الزاوية EBF تساوي 45 درجة.
وبالتالي، زاوية BED = 45 درجة + زاوية FED.
تذكر، cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
دعونا نطبق قانون جيب التمام مرة أخرى، هذه المرة على المثلث BED.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD هو ضلع المربع المعني، لذا BD^2 هي مساحة هذا المربع، والتي أظهرنا أنها 369.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
أنت فني ألعاب نارية مسؤول عن عرض الألعاب النارية الليلي في مدينة ملاهي. تلقيتَ صواريخًا حديثة الطراز من أوروبا، وتختبر أحدها لضبط توقيته على أنغام موسيقى العرض.
يُطلق صاروخ الألعاب النارية عموديًا لأعلى بتسارع ثابت قدره 4 م² حتى ينفد وقوده الكيميائي. ثم تتباطأ سرعته بفعل الجاذبية حتى يصل إلى أقصى ارتفاع له وهو 138 مترًا، حيث ينفجر.
بافتراض عدم وجود مقاومة للهواء وتسارع الجاذبية يساوي 9.8 متر في الثانية في الثانية، ما المدة التي يستغرقها الصاروخ للوصول إلى أقصى ارتفاع له؟
يترك:
t = الوقت منذ نفاد وقود الصاروخ.
r = الوقت الذي استمر فيه وقود الصاروخ.
سأعبّر عن التسارع باتجاه تصاعدي. إذًا، التسارع بعد احتراق وقود الصاروخ يساوي -9.8.
للتذكير، تكامل التسارع هو السرعة، وتكامل السرعة هو الموقع. لنحسب الموقع بالنسبة للأرض.
عندما تم إطلاق الصاروخ لأول مرة، علمنا أن التسارع هو 4.
بأخذ التكامل، فإن سرعة الصاروخ بعد r ثانية تساوي 4r.
بأخذ تكامل السرعة نحصل على موقع الصاروخ بعد r ثانية من 2r 2 .
الآن دعونا ننظر إلى ما يحدث بعد احتراق وقود الصاروخ.
لقد علمنا أن تسارع الجاذبية يساوي -9.8.
سرعة الجاذبية الأرضية عند اللحظة t هي -9.8t. ومع ذلك، لها أيضًا سرعة تصاعدية قدرها 4r من الصاروخ.
ليكن v(t) = السرعة عند الزمن t
v(t) = -9.8t + 4r
سيصل الصاروخ إلى أقصى ارتفاع عندما يكون v(t) = 0. دعنا نحل ذلك.
v(t) = 0 = -9.8t + 4r
4r = 9.8t
t = 40/98 r = 20r/49.
بمعنى آخر، مهما كان الوقت الذي يستمر فيه وقود الصاروخ، فإن الصاروخ سيستمر في السفر إلى الأعلى لمدة 20/49 من ذلك الوقت.
وقد أعطينا أيضًا المسافة المقطوعة عند أقصى ارتفاع تم تحقيقه وهو 138.
لنأخذ تكامل v(t) للحصول على صيغة المسافة المقطوعة، والتي سنسميها d(t).
d(t) = -4.9t 2 + 4rt + c، حيث c هو ثابت التكامل.
كما أوضحنا سابقًا، قطع الصاروخ مسافة 2r 2 عند احتراق الوقود، لذا لا بد أن يكون هذا ثابت التكامل. وهذا يعطينا:
d(t) = -4.9t 2 + 4rt + 2r 2
نحن نعلم أن الارتفاع الأقصى 138 تم الوصول إليه في الوقت 20r/49، لذا دعنا ندخل t=20r/49 في المعادلة لحل r:
د ((20 ص / 49) = -4.9 ((20 ص / 49) 2 + 4 ص (20 ص / 49) + 2 ص 2 = 138
r 2 *(-1960/2401 + 80/49 + 2) = 138
r 2 = 49
ر = 7
لذا، فإن وقود الصاروخ استمر لمدة سبع ثوان.
نحن نعلم بالفعل أن الصاروخ استمر في الارتفاع لمدة 20/49 من ذلك الوقت، وهو ما يعادل 140/49 = تقريبًا 2.8571 ثانية.
وبالتالي، فإن الوقت من الإطلاق إلى السرعة القصوى هو 7 + 140/49 = 483/49 = حوالي 9.8571 ثانية
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ما هو العدد المتوقع لرميات حجري نرد لتحقيق مجموع من ٢ إلى ١٢؟ يُرجى استخدام حساب التفاضل والتكامل لحل مشكلتك.
تذكر أن احتمال الحصول على مجموع ٢ هو ١/٣٦. في عدد t من الرميات، تكون الرميات المتوقعة بمجموع ٢ هي t/٣٦. افترض أن الوقت بين الرميات موزع بشكل أسّي بمتوسط t/٣٦. يوضح توزيع بواسون أن احتمال عدم وجود رميات بمجموع ٢ هو exp(-t/٣٦).
تذكر أن احتمال الحصول على مجموع 3 هو 2/36 = 1/18. وبنفس المنطق، يُخبرنا توزيع بواسون أن احتمال عدم الحصول على مجموع 3 هو exp(-t/18).
تذكر أن احتمال الحصول على مجموع ٤ هو ٣/٣٦ = ١/١٢. وبنفس المنطق، يُخبرنا توزيع بواسون أن احتمال عدم الحصول على مجموع ٤ هو exp(-t/١٢).
تذكر أن احتمال الحصول على مجموع ٥ هو ٤/٣٦ = ١/٩. وبنفس المنطق، يُخبرنا توزيع بواسون أن احتمال عدم الحصول على مجموع ٥ هو exp(-t/9).
تذكر أن احتمال الحصول على مجموع 6 هو 5/36. وبنفس المنطق، يُخبرنا توزيع بواسون أن احتمال عدم الحصول على مجموع 6 هو exp(-5t/36).
تذكر أن احتمال الحصول على مجموع ٧ هو ٦/٣٦ = ١/٦. وبنفس المنطق، يُخبرنا توزيع بواسون أن احتمال عدم الحصول على مجموع ٧ هو exp(-t/6).
احتمالات 8 إلى 12 هي نفسها احتمالات 2 إلى 6.
وبالتالي، فإن احتمال أن يتم طرح كل إجمالي في وحدات t مرة واحدة على الأقل هو:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
احتمال عدم حدوث أي رمية إجمالية على الأقل في وحدات زمنية t هو 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
للحصول على الوقت المتوقع بدون مجموع واحد على الأقل نقوم بدمج الدالة أعلاه من 0 إلى ما لا نهاية.
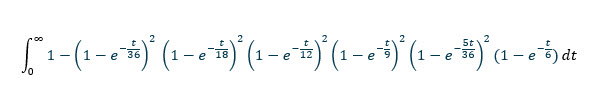
سوف تقوم الآلة الحاسبة التكاملية (أوصي بهذه الآلة ) بحل هذه المسألة بسهولة على النحو التالي: 769767316159/12574325400 = تقريبًا 61.2173847639572 لفة.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
المكعب هو كتلة ثلاثية الأبعاد، تتكون من مربعات وحدوية.
يتكون متوازي المستطيلات (أ × ب × ج) من مكعبات وحدوية متطابقة (أ ب ج)، مثل مكعب روبيك 3×3×3. قسّم المكعبات إلى نوعين متنافيين. المكعبات الخارجية هي التي تُشكّل أوجه متوازي المستطيلات؛ والمكعبات الداخلية مغلقة تمامًا. على سبيل المثال، يحتوي متوازي المستطيلات الموضح في الصورة على 74 مكعبًا خارجيًا و10 مكعبات داخلية.
أعط أبعاد جميع المكعبات بحيث يكون عدد المكعبات الخارجية مساويًا لعدد المكعبات الداخلية.
- 5 × 13 × 132
- 5 × 14 × 72
- 5 × 15 × 52
- 5 × 16 × 42
- 5 × 17 × 36
- 5 × 18 × 32
- 5 × 20 × 27
- 5 × 22 × 24
- 6 × 9 × 56
- 6 × 10 × 32
- 6 × 11 × 24
- 6 × 12 × 20
- 6 × 14 × 16
- 7 × 7 × 100
- 7 × 8 × 30
- 7 × 9 × 20
- 7 × 10 × 16
- 8 × 8 × 18
- 8 × 9 × 14
- 8 × 10 × 12
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ليكن 0 < a < b. أيهما أكثر a^b أم b^a؟
تعتمد الإجابة على (أ) و(ب) على وجه التحديد، ولكن هناك قاعدتان عامتان ستعالجان معظم المواقف.
إذا كان a > e، فإن a^b > b^a
إذا كان b < e، فإن a^b < b^a
إذا كان a < e و b > e، إذن لا توجد معلومات كافية لتحديد ذلك.
وهنا الحل (PDF).
أُلقيت قنبلة يدوية في حفرة عميقة. في المتوسط، تنفجر القنبلة في ست ثوانٍ. يتميز الوقت المتبقي حتى انفجارها بخاصية عدم التذكر، حيث إن احتمالية حدوث انفجار في أي لحظة تكون ثابتة دائمًا، ولا تعتمد على المدة التي انقضت منذ سحب الدبوس. بمعنى آخر، يتبع عمرها الافتراضي التوزيع الأسّي. افترض تسارعًا قدره 32 قدمًا في الثانية.
تخيل برنامجًا للمسابقات، فيه متسابقان أنانيان ومنطقيان بارعان. إليك القواعد.
- يقوم المضيف بوضع مليون دولار على الطاولة بين المتسابقين.
- يُطلب من المتسابق أ تقديم اقتراح حول كيفية تقسيم الأموال بين المتسابقين.
- سيتم الطلب من المتسابق ب قبول أو رفض الاقتراح.
- إذا قبل المتسابق ب الاقتراح، فإنهما يقومان بتقسيم الأموال بهذه الطريقة وتنتهي اللعبة.
- إذا رفض المتسابق ب الاقتراح، فسوف يقوم المضيف بإزالة 10% من المبلغ الموجود حاليًا على الطاولة.
- ثم يطلب المضيف من المتسابق ب تقديم اقتراح، ويحصل المتسابق أ على نفس الفرصة لقبوله أو رفضه.
- إذا قبل المتسابق (أ) الاقتراح، يُقسّم المبلغ بهذه الطريقة وتنتهي اللعبة. إذا رفضه، يحصل المُضيف على ١٠٪ أخرى من المبلغ المتبقي على الطاولة. ثم عُد إلى الخطوة ٢ واستمر في التكرار حتى يتم قبول الاقتراح.
السؤال هو كيف ينبغي للمتسابق أ أن يقترح تقسيم الأموال في دوره الأول؟
ينبغي أن يقترح الاحتفاظ بـ ١٠/١٩ من المال لنفسه، ناقصًا بنسًا واحدًا، وعرض على بـ ٩/١٩ من المال، زائد بنس واحد. بمعنى آخر:
أ: 526,315.78 دولارًا
ب: 473,684.22 دولارًا
المفتاح هو أن A يجب أن يضع B أقرب ما يمكن إلى نقطة اللامبالاة.
لنسمِّ نسبة الرهان إلى رصيد اللاعب الآخر r. إذا قبل B العرض، فسيحصل على r × 1,000,000 دولار.
إذا رفض ب العرض، يحصل المضيف على ١٠٪. بعد ذلك، سيتمتع بميزة موقع، وسيعرض على المتسابق أ حصة من r، ويحتفظ بـ ١-r لنفسه.
حل ل...
r×1,000,000 = (1-r)×900,000.
r×1,900,000 دولار = 900,000 دولار.
ر = 900,000 دولار/1,900,000 دولار = 9/19.
لا يريد أ أن يكون ب غير مبالٍ تمامًا، خشية أن يختار عشوائيًا ويحصل على فرصة فوز المضيف بالجائزة الكبرى. لذا، على أ أن يدفع له البنس الإضافي ويعرض عليه (9/19) × 1,000,000 دولار + 0.01 دولار = 473,684.22 دولارًا.
أ: 526,315.78 دولارًا
ب: 473,684.22 دولارًا
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
تقع مدينتان، فونتلروي وساوثوورث، على ضفة قناة مباشرة. تتنقل عبّارتان ذهابًا وإيابًا بين المدينتين طوال اليوم. تسافر العبّارتان بسرعات مختلفة. في الوقت نفسه، تنطلقان من كل مدينة.
أول مرة يعبرون فيها كانت على بُعد 5 أميال من ساوثوورث. ثاني مرة يعبرون فيها على بُعد 3 أميال من فونتليروي. افترضوا أنه لا يوجد وقت للتحميل والتفريغ، لكن كلاهما انعطفا فجأةً. افترضوا أيضًا أنهما يسيران في خط مستقيم.
ما هي المسافة بين المدينتين؟
دع t 2 = الوقت حتى العبور الثاني
r = نسبة سرعة العبارة التي تغادر فونتليروي في البداية إلى سرعة العبارة التي تغادر ساوثوورث في البداية.
ج = مسافة القناة بين مدينتين.
علمنا أن أول عبور لهم كان على بُعد خمسة أميال من ساوثوورث. للتعبير عن ذلك بالصيغ التالية:
ج-5 = ر*ت 1
5 = t1
بمعادلة t1 نحصل على:
c-5 = 5r، أو r = (c-5)/5
علمنا أيضًا أن عبورهم الثاني كان على بُعد ثلاثة أميال من فونتليروي. للتعبير عن ذلك بالصيغ التالية:
3ج - 3 = r*t 2
ج+3 = ت 2
بمعادلة t 2 نحصل على:
2ج - 3 = r*(ج+3)
استبدل r=(c-5)/5
2ج-3 = [(ج-5)/5] * (ج+3)
10 ج - 15 = ج^2 - 2 ج - 15
ج^2 - 12ج = 0 ج - 12 = 0 ج = 12
ويبلغ طول القناة 12 ميلاً.
في الرسم التخطيطي التالي، ما هي مساحة المنطقة الزرقاء؟
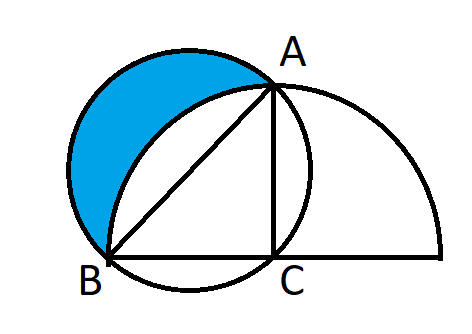
انقر على الزر أدناه للحصول على الإجابة.
وهنا الحل الخاص بي (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في بطولة الشطرنج، يلعب كل متسابق مباراة ضد جميع المتسابقين الآخرين. يحصل كل متسابق على نقطة واحدة عن كل مباراة يفوز بها، و٠.٥ نقطة عن كل مباراة متعادلة، و٠ نقطة عن كل جولة يخسرها.
وفي نهاية البطولة، نرى أن جميع المتسابقين حصلوا على عدد مختلف من النقاط وأن المتسابق الأخير في ترتيب النقاط هزم كلًا من المتسابقين الثلاثة الأوائل.
وبناءً على ذلك، ما هو الحد الأدنى لعدد المتسابقين المشاركين في البطولة؟
دعونا نطلق على عدد اللاعبين n.
أعتقد أن صاحب المركز الأخير حقق ثلاثة انتصارات فقط ضد أفضل ثلاثة لاعبين، وخسر جميع المباريات الأخرى. هذا يمنحه ثلاث نقاط.
ثم أحسب كل لاعب لاحق، حسب ترتيب النقاط، بفارق ٠.٥ نقطة عن سابقه في الترتيب. هذا يمنح اللاعب الأعلى ترتيبًا ٣+(ن-١)/٢ نقطة.
بأخذ مجموع 3 إلى 3+(n-1)/2، بمقدار نصف نقطة لكل خطوة، نحصل على (((n+5)*(n+6)/2)-15)/2.
إجمالي المباريات التي لعبها n لاعب هو n*(n-1)/2، حيث يلعب كل لاعب ضد الآخر مرة واحدة. تُحسب نقطة واحدة في كل مباراة، وهو أيضًا إجمالي النقاط المكتسبة بين جميع اللاعبين.
ثم حل ل n:
(((ن+5)*(ن+6)/2)-15)/2 = ن*(ن-1)/2
((ن+5)*(ن+6)/2)-15 = ن*(ن-1)
(ن+5)*(ن+6)/2 = ن*(ن-1) + 15
(ن+5)*(ن+6) = 2*ن*(ن-1) + 30
ن^2 + 11ن + 30 = 2ن^2 - 2ن + 30
ن^2 + 11ن = 2ن^2 - 2ن
ن + 11 = 2ن-2
ن=13
يوضح الجدول التالي كيفية حدوث ذلك. يُظهر نص الجدول الفائز في جميع المباريات الـ 78.
الجدول التالي يبين عدد النقاط لكل لاعب.
إجمالي النقاط حسب اللاعب
| لاعب | نقاط |
|---|---|
| 13 | 3 |
| 12 | 3.5 |
| 11 | 4 |
| 10 | 4.5 |
| 9 | 5 |
| 8 | 5.5 |
| 7 | 6 |
| 6 | 6.5 |
| 5 | 7 |
| 4 | 7.5 |
| 3 | 8 |
| 2 | 8.5 |
| 1 | 9 |
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ما هي الطريقة الأكثر فعالية لتكديس قذائف المدفع، في شكل هرم ذي قاعدة مربعة، مثل أهرامات مصر، أو مثلث الشكل، لتشكيل رباعي السطوح؟


فيما يلي بعض الصيغ التي قد يجدها القارئ مفيدة:
قم بالتمرير إلى الأسفل للحصول على إجابتي والحلي.
عندما تقول "فعال" فسوف أفترض أنك تقصد ما هو الذي يحتوي على أقل قدر من المساحة المهدورة بين قذائف المدفع.
لتبسيط الأمور، ولتحديد حجم أيٍّ من الهرمين، لنستخدم مركز الكرات الواقعة في زوايا الهرم. لنفترض أن n هو عدد قذائف المدفع في أحد جوانب قاعدة أيٍّ من الهرمين.
دعونا ننظر إلى الهرم ذو القاعدة المربعة أولاً.
عدد قذائف المدفع في الهرم بأكمله هو 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ... + n 2 = n*(n+1)*(2n+1)/6.
الآن، لنوجد ارتفاع هذا الهرم المربع عندما يكون أحد أضلاع قاعدته n. كما هو موضح في الصورة، فإن الأضلاع (باستثناء القاعدة المربعة) مثلثات متساوية الأضلاع. وبالتالي، يكون ارتفاع الزاوية المائلة n أيضًا. المسافة من إحدى زوايا القاعدة إلى الزاوية المقابلة لها هي n*sqrt(2). وبالتالي، تكون المسافة من زاوية القاعدة إلى مركزها n*sqrt(2)/2. ليكن الارتفاع h. لنفترض أن المثلث القائم الزاوية يتكون من الارتفاع، والمسافة من زاوية القاعدة إلى مركزها، وارتفاع الزاوية المائلة.
h 2 + (n*sqrt(2)/2) 2 = n 2
ح = ن*الجذر التربيعي(2)/2.
تذكر أن حجم الهرم هو القاعدة × الارتفاع / 3. هذا يُعطي حجم الهرم:
ن 2 * ن* جذر(2)/2 * (1/3) = ن 3 *جذر(2)/6.وبالتالي فإن نسبة الكرات إلى الحجم هي [n*(n+1)*(2n+1)/6] / [n 3 *sqrt(2)/6] = sqrt(2)*n*(n+1)*(2n+1)/(2*n 3 ) = sqrt(2)*(n+1)*(2n+1)/(2*n 2 )
والآن دعونا نلقي نظرة على الهرم ذو القاعدة المثلثة.
عدد قذائف المدفع في الهرم بأكمله هو 1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6.
الآن، لنوجد مساحة القاعدة. تذكر أن أضلاع مثلث ذي أبعاد 30-60-90 تتناسب طرديًا مع 1/2، وsqrt(3)/2، و1. بناءً على ذلك، ليس من الصعب إيجاد ارتفاع مثلث متساوي الأضلاع طول ضلعه n هو n*sqrt(3)/2. هذا يجعل مساحة القاعدة n 2 *sqrt(3)/4.
المسافة من زاوية القاعدة إلى مركزها هي الجذر التربيعي (3)/3. وبمعرفة ذلك، والارتفاع المائل للهرم (1)، يمكننا استخدام فيثاغورس لإيجاد ارتفاع الهرم بالصيغة الجذر التربيعي (6)/3.
يمكننا الآن إيجاد حجم الهرم على النحو التالي: القاعدة * الارتفاع / 3 = (n 2 * sqrt(3) / 4) * (n * sqrt(6) / 3) * (1/3) = n 3 * sqrt(18) / 36 = n 3 * sqrt(2) / 12.
وبالتالي فإن نسبة الكرات إلى الحجم هي [n*(n+1)*(n+2)/6] / [n 3 *sqrt(2)/12] = sqrt(2)*n*(n+1)*(2n+1)/(2*n 3 ) = sqrt(2)*(n+1)*(n+2)/n 2
فيما يلي مقارنة بين نسبة الكرات إلى الحجم:
- القاعدة المربعة: sqrt(2)*(n+1)*(2n+1)/(2*n 2 )
- قاعدة المثلث: sqrt(2)*(n+1)*(n+2)/n 2
دعونا نقسم النسبتين على sqrt(2)*(n+1)/n 2 :
- القاعدة المربعة: (2ن+1)/2 = ن+0.5
- قاعدة المثلث: n+2
كلما ازدادت قيمة n، ستقترب نسبة الكرات إلى الحجم من n لكلا الهرمين. بمعنى آخر، كلما زاد عدد كرات المدفع، زادت كفاءتها.
بالنظر إلى حجم قذيفة المدفع، فإن الكفاءة في كلا الهرمين، والتي تعرف بأنها نسبة حجم قذيفة المدفع إلى الحجم الإجمالي، تقترب من pi*sqrt(2)/6 =~ apx. 74.05%.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لأي عدد كبير مُعطى، ما هو متوسط المسافة بين الأعداد الأولية القريبة منه؟ وكم عدد الأعداد الأولية الأصغر منه؟
تقدير جيد جدًا لمتوسط المسافة بين الأعداد الأولية بالقرب من أي عدد كبير n هو ln(n). ومن اللافت للنظر مدى جودة هذا التقدير.
كدليل على ذلك، يوضح الجدول التالي نطاق أول 15 مليون عدد أولي، في مجموعات من مليون عدد. يوضح الجدول متوسط المسافة بين الأعداد الأولية وتقدير متوسط المسافة. التقدير هو اللوغاريتم الطبيعي لمتوسط أكبر وأصغر عدد أولي في النطاق. على سبيل المثال، للمجموعة الخامسة عشرة من مليون عدد أولي، يكون ln((256,203,221+275,604,541)/2).
متوسط المسافة بين الأعداد الأولية
| أول رئيس في النطاق | آخر رئيس في النطاق | الأعداد الأولية في النطاق | متوسط المسافة | تقدير | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | مليون | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | مليون | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | مليون | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | مليون | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | مليون | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | مليون | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | مليون | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | مليون | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | مليون | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | مليون | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | مليون | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | مليون | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | مليون | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | مليون | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | مليون | 19.40132 | 19.39864545 |
المصدر: الفجوات بين الأعداد الأولية في صفحات الأعداد الأولية.
للحصول على عدد الأعداد الأولية تحت أي عدد معطى، نبدأ بدمج تقدير متوسط المسافة لـ ln(n). سيعطينا هذا مجموع متوسط المسافات بين الأعداد الأولية حتى أي عدد n.
ما هو تكامل f(n)=ln(n)؟ تذكر أن التكامل بالتجزيء يُخبرنا:
تكامل f(n)*g'(n) dn = f(n)*g(n) - تكامل (f'(n)*g(n)) dn
ليكن f(n)=ln(n) وg'(n)=1. عندها، f'(n)=1/n وg(n)=n. تكامل ln(n) سيكون ln(n)*n - تكامل ((1/n)*n) = ln(n)*n - n = n*(ln(n)-1)
إذا قسمنا n*(ln(n)-1) على n، نحصل على متوسط المسافة بين الأعداد الأولية لمجموعة الأعداد من 2 إلى n. وهذا هو ln(n)-1.
إذا قسمنا n على هذه المسافة المتوسطة بين الأعداد الأولية، نحصل على متوسط عدد الأعداد الأولية تحت n، والذي يساوي n/(ln(n)-1).
كدليل، يُظهر الجدول التالي عدد الأعداد الأولية تحت أعداد كبيرة مختلفة والقيمة المُقدّرة. يُرجى المعذرة عن دقة الأرقام الخمسة عشر المعنوية، وهي أقصى ما يسمح به برنامج إكسل. رجاءً، يُمكن لأحدكم إنشاء جدول بيانات يستوعب المزيد.
متوسط المسافة بين الأعداد الأولية
| ن | الأعداد الأولية تحت n | ن/(لن(ن)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 100,000 | 9,592 | 9,512 |
| مليون | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 100,000,000 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 455,052,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
المصدر: كم عدد الأعداد الأولية الموجودة؟ في صفحات الأعداد الأولية.
الشكل أعلاه هو شكل تسعي يبلغ طول ضلعه واحدًا.
أيهما أكثر، AB+AC أم AE؟
تم أخذ هذه المشكلة من إصدار مارس 2021 من نشرة مينسا.
وهنا الحل لهذه المشكلة. (PDF)
كيف يمكنني بسهولة العثور على الجذر التربيعي لأي عدد مكون من ثلاثة أو أربعة أرقام، على افتراض أن الإجابة عدد صحيح؟
يوضح الجدول التالي الأرقام من 0 إلى 9، ومربع كل رقم والرقم الأخير من هذا المربع.
الرقم الأخير من الأعداد المربعة
| إبداعي رقم | مربع | الرقم الأخير من المربع |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
لاحظ أن الأرقام هي مربعات زوجية تنتهي دائمًا بـ 0، 1، 4، 5، 6، أو 9. وهذا ينطبق على جميع المربعات، لأن الرقم الأخير من الرقم الأصلي يُحدد الرقم الأخير من المربع.
الخطوة ١: بناءً على الرقم الأخير من الجذر التربيعي، يمكننا استخدام الجدول التالي لتحديد الرقم الأخير من الجذر التربيعي. على سبيل المثال، إذا كان الرقم ٢٨٠٩ هو الرقم، فإن الرقم الأخير من الجذر التربيعي هو ٣ أو ٧.
الرقم الأخير من الرقم الأصلي
| الرقم الأخير من الجذر التربيعي | الرقم الأخير من المربع |
|---|---|
| 0 | 0 |
| 1 | 1 أو 9 |
| 4 | 2 أو 8 |
| 5 | 5 |
| 6 | 4 أو 6 |
| 9 | 3 أو 7 |
الخطوة الثانية: بعد ذلك، خذ الرقم الأصلي واحذف الرقمين الصحيحين. على سبيل المثال، إذا كان الرقم الأصلي ٢٨٠٩، فاستخدم ٢٨.
الخطوة ٣: أوجد أصغر عدد مربع أصغر من أو يساوي ناتج الخطوة ٢. ثم احسب الجذر التربيعي لهذا العدد. على سبيل المثال، أصغر عدد مربع أصغر من ٢٨ هو ٢٥. احسب الجذر التربيعي لـ ٢٥ لتحصل على ٥.
إذا لم تحفظ المربعات حتى الرقم 100، فيمكنك استخدام الجدول التالي.
الجزء الأول من الجذر التربيعي
| الخطوة 2 | الخطوة 3 |
|---|---|
| من 1 إلى 3 | 1 |
| من 4 إلى 8 | 2 |
| من 9 إلى 15 | 3 |
| من 16 إلى 24 | 4 |
| من 25 إلى 35 | 5 |
| من 36 إلى 48 | 6 |
| من 49 إلى 63 | 7 |
| من 64 إلى 80 | 8 |
| من 81 إلى 99 | 9 |
الخطوة 4: إذا كانت النتيجة من الخطوة 1 هي 0 أو 5، فضع ذلك بعد النتيجة من الخطوة 3 وقد انتهيت.
بخلاف ذلك، ليكن a = الناتج من الخطوة 3. ليكن b=a×(a+1). على سبيل المثال، إذا كانت النتيجة من الخطوة 3 هي 5، فإن b=5×6=30.
الخطوة 5: إذا كان b < a، فإن الرقم الأخير من الجذر التربيعي هو الأصغر من الاحتمالات من الخطوة 1. وإلا، إذا كان b >= a، فإنه يكون الأكبر من الاحتمالين.
الخطوة 6: للحصول على الجذر التربيعي، خذ النتيجة من الخطوة 3 ثم اتبعها بالنتيجة من الخطوة 5. بمعنى آخر 10 × (الخطوة 3) + الخطوة 5.
دعونا نلقي نظرة على بعض الأمثلة:
أوجد الجذر التربيعي لـ 256.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 4 أو 6.
- الخطوة 2: حذف الرقمين الأخيرين، نحصل على 2.
- الخطوة 3: أصغر مربع أقل من أو يساوي 2 هو 1. الجذر التربيعي لـ 1 هو 1.
- الخطوة 4: 1*(1+1) = 2.
- الخطوة 5: النتيجة من الخطوة 4 تساوي النتيجة في الخطوة 2، لذلك نستخدم الخيار الأكبر من الخطوة 1 كالرقم الأخير، وهو 6.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 1 و 6 = 16.
أوجد الجذر التربيعي لـ 1369.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 3 أو 7.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 13.
- الخطوة 3: أصغر مربع أقل من أو يساوي 13 هو 9. الجذر التربيعي لـ 9 هو 3.
- الخطوة 4: 3*(1+3) = 12.
- الخطوة 5: النتيجة من الخطوة 2 أكبر من تلك في الخطوة 4، لذلك نستخدم الخيار الأكبر من الخطوة 1 كالرقم الأخير، وهو 7.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 3 و 7 = 37.
أوجد الجذر التربيعي لـ 2704.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 2 أو 8.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 27.
- الخطوة 3: أصغر مربع أقل من أو يساوي 27 هو 25. الجذر التربيعي لـ 25 هو 5.
- الخطوة 4: 5*(1+5) = 60.
- الخطوة 5: النتيجة من الخطوة 2 أقل من النتيجة في الخطوة 4، لذلك نستخدم الخيار الأصغر من الخطوة 1 كالرقم الأخير، وهو 2.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 5 و 2 = 52.
أوجد الجذر التربيعي لـ 5625.
- الخطوة 1: الرقم الأخير من الجذر التربيعي هو 5.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 56.
- الخطوة 3: أصغر مربع أقل من أو يساوي 56 هو 49. الجذر التربيعي لـ 49 هو 7.
- الخطوة 4: النتيجة من الخطوة 1 هي 0 أو 5، لذا فإن الإجابة هي النتيجة من الخطوة 3 المضافة إلى الخطوة 1: 7 و 5 = 75
أوجد الجذر التربيعي لـ 6561.
- الخطوة 1: الرقم الأخير هو 1 أو 9.
- الخطوة الثانية: إذا حذفنا الرقمين الأخيرين، نحصل على 65.
- الخطوة 3: أصغر مربع أقل من أو يساوي 65 هو 64. الجذر التربيعي لـ 64 هو 8.
- الخطوة 4: 8*(1+8) = 72.
- الخطوة 5: النتيجة من الخطوة 2 أقل من النتيجة في الخطوة 4، لذلك نستخدم الخيار الأقل من الخطوة 1 كالرقم الأخير، وهو 1.
- الخطوة 6: الجذر التربيعي هو النتيجة من 3 المضافة إلى النتيجة من الخطوة 5، والتي تصل إلى 8 و 1 = 81.
يمكنك مشاهدة عرض توضيحي لهذه الطريقة على اليوتيوب .
ما هي مساحة الشكل الخماسي المنتظم الذي طول ضلعه 1؟
انقر على المربع أدناه للحصول على الإجابة.
انقر على المربع أدناه للحصول على تلميح.
[المفسد=تلميح]
انظر إلى الصورة أعلاه. AC = CD.
[/spoiler]وهنا الحل الخاص بي (PDF)
في يومٍ هادئ، أخذ تشارلي زورقه إلى النهر وجدف عكس التيار. يجدف دائمًا بنفس السرعة (أي أنه لو تجاهلنا التيار، لكان دائمًا بنفس السرعة). بعد ميل من انطلاقه، سقطت قبعته في النهر. بعد عشر دقائق، أدرك أنها مفقودة، فانعطف على الفور ليلحق بها في اتجاه مجرى النهر. لحق تشارلي بقبعته في نفس المكان الذي انطلق منه.
ما مدى سرعة التيار؟
انقر على الزر أدناه للحصول على الإجابة.
وهنا الحل الخاص بي (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
السؤال التالي يتعلق برهان شريطي. يُستخدم رقم تسلسلي أمريكي عشوائي لأي ورقة نقدية. يختار اللاعب أي ثلاثة أرقام من 0 إلى 9. يجب عليه اختيار ثلاثة أرقام مختلفة. تُحسب الأرباح بناءً على عدد الأرقام الثلاثة المختارة التي تظهر مرة واحدة على الأقل في الرقم التسلسلي.
على سبيل المثال، إذا اختار اللاعب ٧-٠-٢ وكان الرقم التسلسلي ٢٢٢٢٧٧٥٥، فهناك تطابقان. لا يهم إن تطابق الرقمان ٢ و٧ عدة مرات.
وفيما يلي الاحتمالات المقدمة:
- 3 مباريات: 5 إلى 1
- 2 مباريات: 1 إلى 1
- مباراة واحدة: 9 إلى 5
- 0 مباراة: 15 إلى 1
ما هي احتمالات الفوز ونسبة ميزة المنزل لكل رهان؟
يوضح الجدول التالي عدد التركيبات الفائزة، واحتمالية الفوز، ونسبة ربح الكازينو لكل رهان. يُظهر العمود الأيمن أن نسبة ربح الكازينو تتراوح بين 7.4% و8.5%.
رهانات الرقم التسلسلي
| المباريات | يدفع | التركيبات | احتمال | حافة المنزل |
|---|---|---|---|---|
| 3 | 5 | 15,426,684 | 0.154267 | 0.074399 |
| 2 | 1 | 45,771,270 | 0.457713 | 0.084575 |
| 1 | 1.8 | 33,037,245 | 0.330372 | 0.074957 |
| 0 | 15 | 5,764,801 | 0.057648 | 0.077632 |
باستخدام كل رقم من 1 إلى 9 مرة واحدة بالضبط، قم بتكوين ثلاثة كسور، كل منها يحتوي على رقم واحد في البسط ورقمين في المقام، بحيث يكون مجموع الكسور الثلاثة هو واحد.
على سبيل المثال، 8/16 + 9/27 + 3/24 تلبي كل الشروط، باستثناء أن المجموع يساوي 23/24، وليس 1.
هناك 60,480 تبديلًا ممكنًا يجب فرزها للعثور على الإجابة. أعترف أنني حاولتُ لمدة ساعة على الأقل بالتجربة والخطأ ولم أجد حلًا.
لذا، كتبتُ برنامجًا لفرز جميع طرق ترتيب الأرقام التسعة (fact(9) = 362,880) واختبرتُها جميعًا. كان الجزء الصعب هو فرز جميع الطرق الممكنة لترتيب الأرقام التسعة. إليك كيفية القيام بذلك باستخدام الفرز المعجمي.
- ضع العناصر التسعة كلها في مصفوفة، مرتبة من الأدنى إلى الأعلى.
- ابحث عن آخر عنصر في المصفوفة بحيث يكون العنصر التالي أكبر. إذا لم يتم العثور على أيٍّ منها، فاخرج من البرنامج.
- ابدأ بالعنصر بعد ذلك من الخطوة 2، وابحث عن العنصر الأخير في المصفوفة الذي يكون أكبر من العنصر من الخطوة 2.
- قم بتبديل العناصر في المصفوفة من الخطوتين 2 و 3.
- قم بعكس العناصر الموجودة في المصفوفة من تلك التي تليها من الخطوة 2 حتى النهاية.
- العودة إلى الخطوة 2
باتباع هذه العملية، ستجد الإجابة الصحيحة ست مرات، مرة واحدة لجميع الطرق الست لترتيب الكسور الثلاثة.
[spoiler=Code]
لقد كتبت الكود التالي لفرز كل رقم من 1 إلى 9 حسب الترتيب المعجمي واختبار كل رقم لمعرفة ما إذا كان حلاً.
void three_fraction(void)
{
int i، x_max، y_max، temp_array[100]، hold، pt؛
int lex_array[] = { 1,2,3,4,5,6,7,8,9 };
عدد العناصر = حجم (مجموعة lex) / حجم (مجموعة lex[0]);
int count = 0؛
bool stop = false؛
ضعف tot3؛
cerr << "عدد العناصر =\t" << num_elements << "\n";
يفعل
{
العد++؛
tot3 = (مزدوج) مصفوفة lex[0] / (مزدوج)(10 * مصفوفة lex[1] + مصفوفة lex[2]);
tot3 += (مزدوج) مصفوفة lex[3] / (مزدوج)(10 * مصفوفة lex[4] + مصفوفة lex[5]);
tot3 += (مزدوج) مصفوفة lex[6] / (مزدوج)(10 * مصفوفة lex[7] + مصفوفة lex[8]);
إذا (tot3 == 1.0)
{
cerr << count << "\t";
cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
}
x_max = -1؛
لـ (i = 0؛ i < (عدد العناصر - 1)؛ i++)
{
إذا (مصفوفة lex[i] < مصفوفة lex[i + 1])
x_max = i؛
}
إذا (x_max >= 0)
{
y_max = 0؛
لـ (i = x_max + 1؛ i < عدد العناصر؛ i++)
{
إذا (مصفوفة lex[x_max] < مصفوفة lex[i])
y_max = i؛
}
عقد = lex_array[x_max]؛
مجموعة ليكس[x_max] = مجموعة ليكس[y_max]؛
lex_array[y_max] = hold؛
إذا (x_max + 1 < num_elements - 1) // عكس
{
لـ (i = x_max + 1؛ i < عدد العناصر؛ i++)
{
مصفوفة مؤقتة[i] = مصفوفة ليكس[i]؛
}
نقطة = 0؛
لـ (i = x_max + 1؛ i < عدد العناصر؛ i++)
{
مصفوفة lex_array[i] = مصفوفة temp[عدد العناصر - 1 - نقطة]؛
pt++;
}
}
}
آخر
توقف = صحيح؛
} بينما (توقف == خطأ)؛
}
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
كان لدى رجل برميل نبيذ سعة 10 جالونات وإبريق. في أحد الأيام، ملأ إبريقًا بالنبيذ ثم ملأ البرميل بالماء. لاحقًا، عندما امتزج النبيذ والماء تمامًا، ملأ إبريقًا آخر وملأ البرميل بالماء مرة أخرى. احتوى البرميل حينها على كميات متساوية من النبيذ والماء.
ما هي سعة الإبريق؟
ليكن j = حجم الإبريق.
بعد ملء الإبريق لأول مرة، تبقى فيه ١٠ جالونات من النبيذ. بعد استبدال النبيذ بالماء، أصبحت نسبة النبيذ إلى البرميل بأكمله (١٠ جالون)/١٠.
بعد أن استخلص الإبريق النبيذ المخفف، تبقى في البرميل عشرة جالونات من النبيذ المخفف. يمكن التعبير عن كمية النبيذ النقي في النبيذ المخفف بالمعادلة التالية:
(10-ج)*((10-ج)/10) = 5
(10-ج)^2 = 50
ج^2 - 20ج + 100 = 50
ج^2 - 20ج + 50 = 0
ج = (20 +/- الجذر التربيعي (400-200))/2
ج = (20 +/- 10*الجذر التربيعي(2))/2
ج = 10 +/- 5*الجذر التربيعي(2)
لا يمكن أن يكون الإبريق أكبر من البرميل، لذلك يجب علينا استخدام الإشارة السالبة:
ج = 10 - 5*sqrt(2) =~ تقريبًا 2.92893218813452 جالون.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
للاحتفال بعيد الشكر، تجلس أنت و19 عالم رياضيات على طاولة دائرية. يرغب الجميع بتناول صلصة التوت البري، وهي أمامك الآن.
أولاً، تُقدّم الصلصة لنفسك. ثم، بدلًا من توزيعها في دائرة، تُمرّرها عشوائيًا للشخص الجالس مباشرةً إلى يسارك أو يمينك. ثم يفعل هو الشيء نفسه، ويُمرّرها عشوائيًا إما إلى الشخص الجالس إلى يساره أو يمينه. يستمر هذا حتى يحصل الجميع، في مرحلة ما، على صلصة التوت البري.
من بين العشرين شخصًا في الدائرة، من لديه أكبر فرصة ليكون آخر من يحصل على صلصة التوت البري؟
دعونا نسمي أحد علماء الرياضيات G. لكي يكون G هو الأخير، يجب حدوث أمرين:
- يجب أن تصل التوت البري أولاً إلى أحد جيران G.
- يجب أن تتحرك التوت البري 19 موضعًا في الاتجاه المعاكس دون أن تصل إلى G أبدًا.
لكي يكون الأخير، يجب أن يصل التوت البري في النهاية إلى أحد الجيران. لذا، احتمال ذلك ١٠٠٪.
إذن، مهما كان احتمال الجزء الثاني، فهو نفسه لكل شخص. وبالتالي، لكل شخص احتمال متساوٍ ليكون الأخير.
إذا لم يكن هذا الشرح واضحًا، فقد حصل جيالمير على هذه المشكلة من موقع fivethirtyeight.com. هنا يشرحون الحل . انتقل للأسفل إلى الجزء الذي يقول "حل لغز ريدلر الكلاسيكي للأسبوع الماضي".
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
وهنا لغز آخر من The Riddler .
يوجد في كيس ١٠٠ كرة زجاجية. كل كرة زجاجية إما حمراء أو زرقاء أو خضراء. إذا سُحبت ثلاث كرات زجاجية من الكيس، فإن احتمالية الحصول على كرة زجاجية واحدة من كل لون هي ٢٠٪. ما عدد الكرات الزجاجية من كل لون في الكيس؟ يُرجى ملاحظة أنني لم أذكر تحديدًا ما إذا كانت الكرات الزجاجية قد سُحبت مع الاستبدال أم بدونه.
لنحاول حل هذه المسألة بافتراض "مع الاستبدال". لنفترض أن r وb وg هي عدد الكرات الحمراء والزرقاء والخضراء على التوالي. عندها، يكون احتمال سحب واحدة من كل لون 6*(r/100)*(b/100)*(g/100). وبجعل هذا الاحتمال مساويًا لـ 0.2، يمكننا القول:
6*(r/100)*(b/100)*(g/100) = 0.2
6*r*b*g = 200000
العدد 6 لا يُقسّم إلى 200,000 بالتساوي. وبالتالي، لا توجد حلول صحيحة ممكنة لـ r*b*g = 33333.333... لذا، يُمكننا استبعاد حالة السحب مع الاستبدال.
الآن، لنجرب افتراض "بدون استبدال". في هذه الحالة، احتمال سحب لون واحد من كل لون هو r*b*g/combin(100,3) = 0.2. نحاول إيجاد حل لذلك...
r*b*g/161700 = 0.2
r*b*g = 32340
التحليل الأولي للعدد 32340 هو 2*2*3*5*7*7*11.
نحتاج إلى توزيع هذه العوامل بين r وb وg، مع جعل r+b+g = 100. على سبيل المثال، يمكننا تجربة:
ر = 2*3*5 = 30
ب = 2*11 = 22
ج = 7*7 = 49
في حين أن هذه تستخدم بشكل صحيح جميع العوامل الأولية، r+b+g = 101، لذا فهي ليست حلاً صالحًا.
أخشى أنني اضطررت إلى كتابة برنامج تكرار القوة الغاشمة للحصول على حل لـ r و b و g ذات القيم 21 و 35 و 44، بأي ترتيب.
السؤال التالي يأتي إلينا من خلال Riddler Express .
لنفترض وجود قواعد اتحاد كرة القدم الأميركي. لنفترض الوضع التالي:
- الفريق الأحمر متأخر بـ 14 نقطة في نهاية المباراة
- الفريق الأحمر سيكون لديه مباراتين أخريين
- لن يكون للفريق الأزرق أي ممتلكات أخرى
- دعونا نتجاهل الأهداف الميدانية والسلامة، حيث يجب على الفريق الأحمر تسجيل هدفين للحصول على فرصة للفوز
- إذا امتدت المباراة إلى وقت إضافي، تكون نسبة فوز كل فريق ٥٠٪. لا يمكن أن تنتهي المباراة بالتعادل.
- احتمالية تسجيل ركلة بنقطة واحدة بعد الهبوط هي 100%.
- احتمال إجراء تحويل بنقطتين هو p.
عند أي قيمة p يجب على الفريق الأحمر أن يكون غير مبالٍ بالركل والذهاب لتحويل نقطتين بعد أول هبوط (الآن متأخرًا بـ 8)؟
دع p = نقطة اللامبالاة بين الذهاب إلى التحويل إلى نقطتين والركلة.
إذا نجحت محاولة التحويل الأولى ذات النقطتين، فيمكن للفريق الأحمر ركل الكرة للمرة الثانية والفوز.
إذا لم تنجح محاولة تحويل النقطتين الأولى، فيجب على الفريق الأحمر المحاولة مرة أخرى بعد الهبوط الثاني ثم الفوز بالمباراة في الوقت الإضافي.
احتمال الفوز، عند محاولة تحويل النقطتين بعد أول هبوط، هو ص + (1-ص)*ص/2. نساوي هذا باحتمال الفوز بنسبة 50% عند الركل بعد أول هبوط، ونحل المعادلة لإيجاد ص.
ص + (1-ص)*ص/2 = 1/2
2ص + (1-ص)*ص = 1
3ص - ص^2 = 1
ص^2 - 3ص + 1 = 0
باستخدام الصيغة التربيعية، حل لـ p:
ص = (3 +/- الجذر التربيعي (5))/2
نختار الخيار السلبي، للحفاظ على p بين 0 و1، للحصول على p = (3-sqrt(2))/2 = apx. 0.381966011250105
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في عمود "اسأل الساحر" السابق ، سُئلتَ عن عدد الرميات المتوقع لتحقيق ١٢ نتيجةً برمي نردين مرتين متتاليتين. في سياق متصل، أرى شخصًا في منتداك يدّعي أنه شهد ١٨ رمية متتالية (بمجموع ١١) على طاولة الكرابس. ما هو عدد الرميات المتوقع لتحقيق ذلك؟
وهنا الحل الخاص بي (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
تم العثور على الإجابة الدقيقة بمساعدة WizCalc .
حقل عشبي على شكل دائرة نصف قطرها 100 متر، محاط بسياج دائري. رُبطت ماعز بسلسلة بخطاف عند نقطة ثابتة على السياج. لمنع الماعز من زيادة وزنه، أراد المزارع التأكد من أنه لا يصل إلا إلى نصف العشب في الحقل. ما هو طول السلسلة المناسب؟
على سبيل المثال، تُمثل الدائرة الحقل العشبي. ويمثل حرف S مكان تثبيت السلسلة على حافة الحقل. الجزء الأصفر من الدائرة هو المكان الذي يمكن للماعز الوصول إليه. أما المنطقة الخضراء فهي بعيدة عن متناول السلسلة. الهدف هو جعل السلسلة على المسافة الصحيحة بحيث يكون الجزآن الأخضر والأصفر متساويين.
يرجى الرجوع إلى الرسم التخطيطي التالي لحل هذه المشكلة.
النقطة Q هي مركز الدائرة العشبية. سلسلة الماعز مربوطة بالنقطة R. يمكن للماعز الوصول إلى جميع المناطق الملونة، بما في ذلك صورتها المعكوسة أسفل الخط PR.
لقد أعطيت أن نصف قطر الدائرة العشبية هو 100، وبالتالي b + c = d = 100.
سأحل هذه المسألة بتعريف كل شيء من حيث (ب). ثم سأجرب (ب) حتى أحقق النتيجة المرجوة، حيث تستطيع الماعز أكل نصف العشب.
لنبدأ بحل e من حيث b. بالنظر إلى مثلث بأضلاعه b وd وe، نستخدم صيغة فيثاغورس:
ب^2 + هـ^2 = د^2
ب^2 + هـ^2 = 10000
هـ = الجذر التربيعي (10000 - ب^2)
الآن، لنحل الدالة f بدلالة b. تذكر أننا نعلم أن b + c = 100، لذا c = 100 - b. باستخدام فيثاغورس:
ج^2 + ه^2 = ف^2
(100-ب)^2 + (10000 - ب^2) = ف^2
و^2 = 10000 - 200ب + ب^2 + 10000 - ب^2
f^2 = 20000 - 200b
f^2 = 100*(200 - 2ب)
f = 10*sqrt(200-2b)
الآن، دعونا نجد مساحة المثلث QRS:
QRS = (1/2)*100*e = 50*sqrt(10000 - b^2)
بعد ذلك، دعنا نجد مساحة شريحة العشب المقطوعة بالزاوية SQR:
tan(SQR) = e/b = sqrt(10000-b^2)/b.
شريحة SQR = أتان (sqrt(10000-b^2)/b)
المنطقة الحمراء تساوي الشريحة SQR ناقص المثلث QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2).
الآن، لنبحث عن المنطقة الزرقاء + الخضراء + الصفراء + البنفسجية. للقيام بذلك، نحتاج إلى إيجاد الزاوية QRS.
tan(QRS) = e/c = sqrt(10000-b^2)/(100-b)
الزاوية QRS = أتان(sqrt(10000-b^2)/(100-b)).
أضف إلى ذلك المنطقة الحمراء، ويصبح لدينا نصف المساحة الإجمالية التي يمكن للماعز أن تأكلها:
أتان(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2).
ضعف ذلك بالنسبة للجزء الموجود أسفل خط PR للحصول على المساحة الإجمالية:
2*أتان(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2).
وتبلغ المساحة الإجمالية للمنطقة العشبية 10000*pi.
الآن، جرّب b حتى تحصل على مساحة كافية لأكل الماعز تساوي 5000*باي. دالة goaleek في إكسل رائعة لمثل هذه المسائل. كيف كان بإمكان أي شخص إنجاز أي شيء قبل جداول البيانات؟ لا أعرف.
وباستخدام هذه الطريقة، ستجد أن b = 32.867402.
ومن هناك يمكننا الحصول على f = طول السلسلة = 115.8728598 متر.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
ما هي الكلمة التي تنصح بها لبدء استخدام Wordle ؟
للإجابة على ذلك، نظرت أولاً إلى تردد كل حرف في كل موضع، استنادًا إلى قائمة حلول Wordle المسموح بها .
تردد الحروف في Wordle
| خطاب | المركز 1 | المركز 2 | المركز 3 | الموضع 4 | المركز 5 | المجموع |
|---|---|---|---|---|---|---|
| أ | 141 | 304 | 307 | 163 | 64 | 979 |
| ب | 173 | 16 | 57 | 24 | 11 | 281 |
| ج | 198 | 40 | 56 | 152 | 31 | 477 |
| د | 111 | 20 | 75 | 69 | 118 | 393 |
| هـ | 72 | 242 | 177 | 318 | 424 | 1233 |
| ف | 136 | 8 | 25 | 35 | 26 | 230 |
| ج | 115 | 12 | 67 | 76 | 41 | 311 |
| ح | 69 | 144 | 9 | 28 | 139 | 389 |
| أنا | 34 | 202 | 266 | 158 | 11 | 671 |
| ج | 20 | 2 | 3 | 2 | 0 | 27 |
| ك | 20 | 10 | 12 | 55 | 113 | 210 |
| ل | 88 | 201 | 112 | 162 | 156 | 719 |
| م | 107 | 38 | 61 | 68 | 42 | 316 |
| ن | 37 | 87 | 139 | 182 | 130 | 575 |
| ا | 41 | 279 | 244 | 132 | 58 | 754 |
| ص | 142 | 61 | 58 | 50 | 56 | 367 |
| س | 23 | 5 | 1 | 0 | 0 | 29 |
| ر | 105 | 267 | 163 | 152 | 212 | 899 |
| س | 366 | 16 | 80 | 171 | 36 | 669 |
| ت | 149 | 77 | 111 | 139 | 253 | 729 |
| يو | 33 | 186 | 165 | 82 | 1 | 467 |
| الخامس | 43 | 15 | 49 | 46 | 0 | 153 |
| و | 83 | 44 | 26 | 25 | 17 | 195 |
| إكس | 0 | 14 | 12 | 3 | 8 | 37 |
| ي | 6 | 23 | 29 | 3 | 364 | 425 |
| ز | 3 | 2 | 11 | 20 | 4 | 40 |
ثم راجعتُ جميع الكلمات في قائمة حلول Wordle، كلٌّ منها مكون من خمسة أحرف مميزة، وقيّمتُها وفقًا لجدول تكرار الحروف أعلاه. منحتُ نقطتين للمطابقة في الموضع الصحيح، ونقطة واحدة للمطابقة في الموضع غير الصحيح. ثم رتّبتُ القائمة، التي ترونها أدناه.
أفضل الكلمات الافتتاحية في Wordle
<!--/عنوان-الصندوق-->| رتبة | كلمة | نقاط متمركزة|
|---|---|---|
| 1 | التحديق | 5835 |
| 2 | نهض | 5781 |
| 3 | حجر الأردواز | 5766 |
| 4 | يرفع | 5721 |
| 5 | انهض | 5720 |
| 6 | أكثر عقلانية | 5694 |
| 7 | كمين | 5691 |
| 8 | غاضب | 5682 |
| 9 | قديمة | 5665 |
| 10 | قفص | 5652 |
| 11 | يتعقب | 5616 |
| 12 | لاحقاً | 5592 |
| 13 | يشارك | 5562 |
| 14 | محل | 5547 |
| 15 | تخويف | 5546 |
| 16 | تغيير | 5542 |
| 17 | رافعة | 5541 |
| 18 | يُحذًِر | 5483 |
| 19 | دامعة | 5479 |
| 20 | سوتيه | 5475 |
| 21 | تقديم الطعام | 5460 |
| 22 | إضافي | 5457 |
| 23 | وحيد | 5452 |
| 24 | تجارة | 5449 |
| 25 | شخير | 5403 |
| 26 | صر | 5403 |
| 27 | الصخر الزيتي | 5392 |
| 28 | الأقل | 5390 |
| 29 | سرق | 5377 |
| 30 | حجم | 5376 |
| 31 | رد فعل | 5376 |
| 32 | بوق | 5368 |
| 33 | تحليل | 5351 |
| 34 | وهج | 5340 |
| 35 | تكفير | 5338 |
| 36 | يتعلم | 5324 |
| 37 | مبكر | 5320 |
| 38 | اتكأ | 5307 |
| 39 | أكثر شحوبًا | 5285 |
| 40 | توهج | 5280 |
| 41 | ممر | 5280 |
| 42 | شاطئ | 5274 |
| 43 | يسرق | 5268 |
| 44 | ترايس | 5267 |
| 45 | نتيجة | 5258 |
| 46 | واضح | 5258 |
| 47 | حيزبون | 5253 |
| 48 | حجر | 5253 |
| 49 | قلب | 5252 |
| 50 | الخاسر | 5251 |
| 51 | تفتق | 5248 |
| 52 | كاره | 5243 |
| 53 | التتابع | 5241 |
| 54 | طبق | 5240 |
| 55 | أعشق | 5239 |
| 56 | صلصة | 5236 |
| 57 | أكثر أمانًا | 5235 |
| 58 | كائن فضائي | 5233 |
| 59 | الطبقة | 5232 |
| 60 | قص | 5231 |
| 61 | مكبس | 5230 |
| 62 | صفارة الإنذار | 5226 |
| 63 | زورق | 5215 |
| 64 | شاير | 5213 |
| 65 | كلوي | 5210 |
| 66 | طبقة | 5206 |
| 67 | تامر | 5200 |
| 68 | كبير | 5196 |
| 69 | لؤلؤة | 5196 |
| 70 | طريق | 5194 |
| 71 | دعامة | 5192 |
| 72 | شريحة | 5178 |
| 73 | منصة | 5171 |
| 74 | نثر | 5170 |
| 75 | بوغ | 5169 |
| 76 | إثارة | 5166 |
| 77 | جمال | 5164 |
| 78 | الطاقة الشمسية | 5152 |
| 79 | جناح | 5150 |
| 80 | مشوي | 5145 |
| 81 | بيرة لاغر | 5130 |
| 82 | طائرة | 5129 |
| 83 | وتد | 5129 |
| 84 | تم التعامل | 5128 |
| 85 | حربة | 5126 |
| 86 | عظيم | 5126 |
| 87 | ايدر | 5123 |
| 88 | تروب | 5116 |
| 89 | برج | 5108 |
| 90 | مداس | 5107 |
| 91 | عبد | 5097 |
| 92 | يغلق | 5090 |
| 93 | حربة | 5090 |
| 94 | شطف | 5088 |
| 95 | سبب | 5087 |
| 96 | ميال | 5087 |
| 97 | طائرة بدون طيار | 5082 |
| 98 | ضوضاء | 5079 |
| 99 | قمة | 5073 |
| 100 | مُتّزِن | 5068 |
حسنًا، ها هي الكلمة التي أوصي باستخدامها في البداية وهي STARE.
ما هو i^i
وهنا الحل الخاص بي (PDF).
أنت ترغب في لعب لعبة تتطلب نردين عاديين سداسيي الأوجه. للأسف، فقدت النرد. ومع ذلك، لديك تسع بطاقات فهرسة، يمكنك تحديدها بالطريقة التي تريدها. يجب على اللاعب اختيار بطاقتين فهرسة عشوائيًا من بين البطاقات التسع، دون استبدال، وحساب مجموع البطاقتين.
قم بتمييز البطاقات على النحو التالي:
1 @ 0.5
1 @ 1.5
2 @ 2.5
1 @ 3.5
2 @ 4.5
1 @ 5.5
1 @ 6.5
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
هل صحيح أن رمي العملة العادلة من المرجح أن يهبط على الجانب الذي بدأ به وجهه لأعلى؟
وتشير الأدلة إلى أن هذا صحيح!
سجل بيرسي دياكونيس وسوزان هولمز من جامعة ستانفورد ١٠٠٠٠ رمية عملة معدنية. استقرت العملة المعدنية على نفس الوجه الذي بدأت به، ووجهها لأعلى، في ٥٠.٨٪ من المرات (المصدر: حل واحد وخمسون بالمائة من النشرة الإخبارية "ما يحدث في العلوم الرياضية" الصادرة عن الجمعية الرياضية الأمريكية). احتمال أن تكون النسبة مرتفعة أو أعلى هو ٥.٤٨٪.
لإثبات ذلك رياضيًا، افترضتُ أن العدد الفعلي لدورات العملة المعدنية يتبع توزيع بواسون. وبشكل أكثر تحديدًا، إذا كان متوسط عدد الدورات m، فإن احتمالية دوران n دورة بالضبط هي exp(-m)*m^n/n!. ولتوضيح توزيع بواسون، يوضح الرسم البياني التالي احتمالية دوران من 0 إلى 25 دورة، بمتوسط 10.
السبب الذي جعلني أختار افتراض بواسون هو أنه يتبع شكل منحنى الجرس القريب لمتوسطات كبيرة بما فيه الكفاية والنتيجة الفعلية لا يمكن أن تنخفض أبدًا عن الصفر.
ثم حسبتُ احتمالية عدد زوجي من أنصاف الدورات (مما يؤدي إلى هبوط نفس الجانب ووجهه لأعلى كموضع البداية) لمتوسطات مختلفة لأنصاف الدورات. يوضح الجدول التالي النتائج لمتوسطات تتراوح بين 0.5 و5.0.
احتمالية عدد الدورات الزوجي والفردي
| الثورات المتوسطة | مجموع زوجي | المجموع الفردي |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
ثم تساءلتُ لماذا كان احتمال العدد الزوجي دائمًا أكبر من ٥٠٪. اتضح أن احتمال العدد الزوجي، بمتوسط m، يمكن التعبير عنه بالمعادلة ٠٫٥ + e^(-٢m)/٢. يجب أن يكون e مرفوعًا للقوة أيًا كان موجبًا، وبالتالي يكون احتمال العدد الزوجي للدورات موجبًا أيضًا.
يمكنك رؤية دليلي على هذه الصيغة هنا .
حل لـ x:
9 × + 12 × = 16 ×
وهنا الحل الخاص بي (PDF).
لقد تم طرح هذه المشكلة ومناقشتها في المنتدى الخاص بي في Wizard of Odds .
لقد استُلهمت هذه المشكلة من مقطع فيديو بعنوان "سؤال أسي صعب" .
يُجري مكتبك، الذي يضم مئة موظف، تبادل هدايا "بابا نويل السري". في هذه المسابقة، تكتب أسماء كل شخص على أوراق منفصلة، وتضعهم جميعًا في قبعات، ثم يسحب كل شخص اسمًا عشوائيًا ليقدم له هدية.
السؤال هو، كم عدد الحلقات المغلقة التي ستكون هناك، في المتوسط؟
مثال على حلقة مغلقة بحجم 4: جوردون يعطي إلى دون، دون يعطي إلى جون، جون الذي يعطي إلى ناثان، وناثان يعطي إلى جوردون.
إن رسم اسمك الخاص سيكون بمثابة حلقة مغلقة بحجم 1.
لنفترض أن هناك موظفًا واحدًا فقط سيحضر حفلة بابا نويل السرية. من البديهي أنه سيختار نفسه، وهكذا نصل إلى حلقة مغلقة.
ثم وصلت موظفة أخرى متأخرة وطلبت الانضمام. أعطوها قائمة بالموظفين اللذين أصبحا الآن. هناك احتمال نصف أن تختار الموظف الأول والنصف الآخر بنفسها. إذا اختارت الموظف الأول، فيمكنها أن تُدمج في حلقته، حيث تشتري للموظف الأول ويشتري لها. إذن، لدينا الآن 1 + 0.5 × 1 = 1.5.
ثم وصلت موظفة ثالثة متأخرة وطلبت الانضمام. أعطوها قائمةً بالموظفين الثلاثة. هناك احتمال بنسبة ٢/٣ أن تختار الموظف ١ أو ٢، وأن تختار هي الثلث. إذا اختارت الموظف ١ أو ٢، فيمكنها الانضمام إلى حلقتهم، حيث تشتري للموظف الذي تختاره، والموظف الذي كان من المفترض أن يشتري له يشتري الآن للثلاثة. إذن، لدينا الآن ١.٥ + (١/٣) = ١١/٦.
ثم وصلت موظفة رابعة متأخرة وطلبت الانضمام. أعطوها قائمة بأسماء الموظفين الأربعة. هناك احتمال بنسبة ثلاثة أرباع أن تختار الموظف من 1 إلى 3، وأن تختار هي الموظف من 1 إلى 3. إذا اختارت الموظف من 1 إلى 3، فيمكنها الانضمام إلى حلقتهم، حيث تشتري للموظف الذي تختاره، والموظف الذي كان من المفترض أن يشتري له يشتري الآن للموظف الرابع. إذن، لدينا الآن 11/6 + (1/4) = 25/12.
استمر في فعل ذلك والإجابة النهائية هي 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5.187377518.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لنفترض أن نصف دائرة نصف قطرها ١، بداخلها مستطيلان متراصان. ما هي أقصى مساحة إجمالية للمستطيلين؟
وهنا الحل الكامل (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
يرجى تجاهل التوائم المتطابقة، وافتراض أن لكل طفل فرصة 50/50 في أن يولد ذكرًا أو أنثى. إذا تم اختيار أطفال عشوائيًا من عائلات بأحجام محددة تتراوح بين 2 و5، فما احتمال أن يكون لدى ولد أو بنت أخت؟
ومن المثير للاهتمام أن الاحتمال هو نفسه بالنسبة لكلا الجنسين، بغض النظر عن حجم الأسرة.
لننظر إلى حجم عائلة مكونة من ثلاثة أفراد، على سبيل المثال. إليك ثماني طرق ممكنة لترتيب الأولاد والبنات:
مكتب الأعمال الأفضل
بي بي جي
بي جي بي
بي جي جي
جي بي بي
جي بي جي
جي جي بي
جي جي جي
إذا اخترتَ أي فتاة عشوائيًا من القائمة أعلاه، فستجد أن من بين ١٢ فتاة، ٩ منهن لديهن أخوات. وينطبق الأمر نفسه على الـ ١٢ ولدًا، ٩ منهم لديهم أخوات. لذا، فإن الاحتمال هو ٩/١٢ = ٣/٤.
الصيغة العامة لاحتمال وجود أخت لأي طفل، حيث يكون عدد الأطفال هو n، هي 1-(1/2) n-1 .
وهنا احتمال وجود أخت حسب العدد الإجمالي للأطفال في العائلة:
- 1:0
- 2: 1/2
- 3: 3/4
- 4: 7/8
- 5: 15/16
- 6: 31/32
من ناحية أخرى، من المنطقي أن يكون الاحتمال متساويًا بين الأولاد والبنات. جنس إخوتك ليس مرتبطًا بجنسك. لذا، حجم العائلة فقط هو المهم، وليس جنسك.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
في الحلقة الرابعة من الموسم السابع والثلاثين من برنامج "الناجي"، كان هناك تحدٍّ لترتيب أربع قطع من الأحجية على شكل مربع ومثلث متساوي الأضلاع. ما هي الأبعاد الدقيقة للقطع المطلوبة لتحقيق ذلك؟
 |  |
أولاً، دعونا نصنع مخططًا مناسبًا ونضع عليه علامات.
فيما يلي مجرد رسم تخطيطي للمثلث المحلول.
بعد ذلك، بافتراض أن طول أضلاع المربع يساوي 1، فإليك فقط طول كل حرف في الرسم البياني أعلاه.
[كابح]أ = د = هـ = ح = 1/2
ب = ز = SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.572145321740575
ج = و = 1-SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.427854678259425
ك = م = 1/الجذر التربيعي(الجذر التربيعي(3)) =~ 0.759835685651592
ن = (3-SQRT(4*SQRT(3)-3))/(2*SQRT(SQRT(3))) =~ 0.386767938902275
ع = (SQRT(4*SQRT(3)-3)-1)/(2*SQRT(SQRT(3))) =~ 0.373067746749317
[/spoiler]وأخيرًا، هنا حلي الكامل (PDF).
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
أنا متأكد من أنك من مُحبي نظرية الانفجار العظيم. من مشاهدي المُفضلة لعبة حجرة ورقة مقص سحلية سبوك. إنها أشبه بلعبة حجرة ورقة مقص بخمسة رموز، بقواعدها التالية:
- ورق يغطي الصخور
- صخرة تسحق سحلية
- السحلية تسمم سبوك
- سبوك يحطم المقص
- المقص يقطع الورق
- السحلية تأكل الورق سبوك يبخّر الصخور
- مقص يقطع رأس السحلية
- ورقة تدحض سبوك
- الصخرة تسحق المقص
سؤالي هو هل يمكن إضافة المزيد من الرموز، بحيث يكون لكل جانب نفس الفرص ضد لاعب عشوائي؟
نعم، أحب هذا المشهد أيضًا! إليكم فيديو له على يوتيوب .
تحتاج إلى عدد فردي من الرموز. نظريًا، يمكنك الحصول على عدد زوجي، ولكن عليك حينها وضع قواعد تؤدي إلى تعادل أزواج معينة من الرموز المختلفة. لا، نريد لعبة حاسمة حيث يكون التعادل فقط إذا لعب كلا اللاعبين نفس الرمز.
الحل أنيقٌ للغاية وسهل الشرح باستخدام عددٍ أوليٍّ من الرموز. دعوني أشرح باستخدام سبعة رموز، كمثال. لنسمِّ الرموز من A إلى G ونمثلها على دائرة، في الرسم التخطيطي التالي.
بعد ذلك، ابدأ بالرمز A، ثم ارسم سهمًا للرمز التالي باتجاه عقارب الساعة. يجب أن يشير السهم إلى الرمز الذي يقع بين الرمزين. تخيل الأمر كما لو أن هذا الرمز قد أُطلق عليه سهم. استمر في الحركة باتجاه عقارب الساعة حتى تصل إلى A. لن يبدو الرسم التخطيطي كما يلي:
بعد ذلك، كرر نفس العملية، ولكن بحركة رمزين باتجاه عقارب الساعة، بدءًا من A. في الواقع، يمكنك البدء من أي مكان تريده. يبدو الرسم التخطيطي الآن كما يلي:
أخيرًا، كرر العملية نفسها، ولكن تخطى ثلاثة رموز باتجاه عقارب الساعة. سيبدو الرسم التخطيطي الآن كما يلي:
لاحظ في هذه المرحلة أن كل رمز يتغلب على ثلاثة رموز أخرى ويتغلب عليه ثلاثة رموز أخرى مختلفة.
هذه الطريقة فعّالة لأي عدد أولي من الرموز، لأنك عند العودة إلى الرمز الأصلي ستكون قد مررت بجميع الرموز. بالنسبة لـ n رمز، ستحتاج إلى تكرار هذه العملية (n-1)/2 مرة.
يمكنك إنشاء لعبة متوازنة بأي عدد فردي من الرموز، ولكنك ستعود إلى الرمز الأصلي بسرعة كبيرة أحيانًا. عند حدوث ذلك، سيتعين عليك إعادة تكرار الحلقات بدءًا من الرموز التي فاتتك.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
تخلط مجموعة دومينو قياسية (٢٨ قطعة) وتسحب قطعة عشوائيًا. تكشف أحد الجوانب بعناية لتجد الرقم ٦. ما احتمال أن يكون هذا هو الرقم ٦ المزدوج؟
لمن لا يعرف لعبة الدومينو، لكل قطعة وجهان، يحمل كل منهما رقمًا من 0 إلى 6. تتكون المجموعة من قطعة دومينو واحدة من كل نوع ممكن. هذا يعني أن جميع الطرق السبع لاختيار الأرقام (combin(7,2)) = 21، بدون استبدال، من أصل 7، بالإضافة إلى جميع الطرق السبع لوضع الرقمين على نفس الوجه.
هنا جميعها 28: 0-0، 0-1، 0-2، 0-3، 0-4، 0-5، 0-6، 1-1، 1-2، 1-3، 1-4، 1-5، 1-6، 2-2-2، 2-3، 2-4، 2-5، 2-6، 3-3، 3-4، 3-5، 3-6، 4-4، 4-5، 4-6، 5-5، 5-6، 6-6.
وبعد توضيح هذا الشرح، إليك الإجابة والحل.
طريقة بسيطة لإعادة صياغة السؤال هي: ما هو احتمال أن يكون لقطعة دومينو مختارة عشوائيًا نفس الرقم على كلا الجانبين؟ الإجابة ببساطة هي 7/28 = 1/4.
قد تقول إن الإجابة يجب أن تكون ١/٧، لأن الجانب الآخر قد يكون أيًا من الأرقام السبعة المحتملة. صحيح أنه قد يكون أيًا من الأرقام السبعة، لكن احتمالية ظهورها ليست متساوية. يجب حساب دومينو ٦-٦ مرتين، لأن له وجهين أحدهما رقم ستة. لذا، يمكن أن يكون الجانب الآخر أيًا من رقمين ستة، ومجموع الأرقام الستة في المجموعة ثمانية. وبالتالي، تكون الإجابة ٢/٨ = ١/٤.
هذا السؤال مطروح ومناقش في منتداي على موقع Wizard of Vegas . السؤال مُهدى لذكرى آلان مندلسون.
قرر آلان وبوب لعب التنس حتى يفوز أحدهما بمباراتين متتاليتين. احتمال فوز آلان في أي مباراة هو ٢/٣. ما احتمال فوزه بالبطولة؟
قرر آلان وبوب لعب التنس حتى يفوز أحدهما بمباراتين متتاليتين. احتمال فوز آلان في أي مباراة هو ٢/٣. ما احتمال فوزه بالبطولة؟
فيما يلي حل الجيل لأي احتمال فوز آلان في لعبة فردية.
دع p = احتمال فوز a.
دع a = احتمال فوز آلان بالبطولة بعد فوزه بالمباراة الأخيرة.
ليكن b = احتمال فوز آلان بالبطولة بعد فوز بوب باللعبة الأخيرة.
(1) أ = ص + (1-ص)*ب
(2) ب = ص*أ
استبدال المعادلة (2) في المعادلة (1):
أ = ص + (1-ص)*با
أ = ص + باسكال - ص 2 *أ
أ - با + ص 2 * أ = ص
أ(1-ص+ص 2 ) = ص
(3) أ = ص/(1-ص+ص 2 )
استبدال المعادلة (3) في المعادلة (2):
ب = ص 2 /(1-ص+ص 2 )
اللعبة الأولى ستحدد ما إذا كان احتمال فوز أ بالبطولة هو أ أو ب:
الإجابة = pa + (1-p)b
= ص 2 /(1-ص+ص 2 ) + (1-ص)*ص 2 /(1-ص+ص 2 )
= (2أ 2 -أ 3 )/(أ 2 -أ+1)
بإدخال a=2/3، نحصل على احتمال الفوز بالبطولة وهو 16/21.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .
لديك سلم طوله 5 أقدام. ترغب في إسناده على الحائط بأعلى ارتفاع ممكن. لكن يوجد صندوق بمساحة 1×1×1 قدم مكعب، يجب وضع السلم فوقه. لا، لا يمكنك تحريك الصندوق. ما أقصى ارتفاع يمكن أن يصل إليه قمة السلم؟
وهنا الحل الخاص بي (PDF).
عند أي قيمة يكون x 1/x هو الحد الأقصى؟
الجواب هو e =~ 2.71828182845905.
هناك، قيمة e^(1/e) =~ 1.44466786100977.
وهنا الحل الخاص بي (PDF).
لاحظت الصحف في عام 1944 هذه المصادفة المذهلة:
هل هذه مصادفة كبيرة أم أن هناك خدعة رياضية؟
إنها خدعة رياضية وأساس خدعة سحرية معروفة.
لكل من كان على قيد الحياة عام ١٩٤٤، كان مجموع عمره (بعد عيد ميلاده) وسنة ميلاده هو ١٩٤٤. تخيل ذلك. إذا كان عمرك س سنة، فأنت مولود في ١٩٤٤-س. المجموع هو س + (١٩٤٤-س) = ١٩٤٤.
إنه نفس الشيء بالنسبة لـ "سنوات الخدمة" في عام 1944. إذا كنت في منصبك لمدة y سنة، فيجب أن تكون قد بدأت في عام 1944-y. y + (1944-y) = 1944.
مجموع ١٩٤٤ + ١٩٤٤ = ٣٨٨٨. يعمل في كل مرة.
ولتحويل هذا إلى خدعة سحرية تعمل في عام 2023، كموضوع لأخذ مجموع الأشياء الأربعة التالية:
- سنة ميلادهم
- كم سيصبح عمرهم هذا العام؟
- عام حدث فيه حدث مهم (مثل ولادة الطفل الأول).
- ذكرى هذا الحدث الهام هذا العام.
سيكون المجموع دائمًا 2023 + 2023 = 4046.
تم طرح هذا السؤال ومناقشته في منتدياتي في Wizard of Vegas .