على هذه الصفحة
مكافأة كرابس
مقدمة
مكافأة الكرابس هي مجموعة من ثلاثة رهانات جانبية موجودة في الكرابس. وهي كالتالي:
- صغير — يفوز اللاعب إذا حصل على مجموع من 2 إلى 6، قبل الحصول على مجموع 7. عادةً ما تدفع المكاسب 30 إلى 1.
- طويل — يفوز اللاعب إذا حصل على مجموع من 8 إلى 12، قبل الحصول على مجموع 7. عادةً ما تدفع المكاسب 30 إلى 1.
- الكل — يفوز اللاعب إذا حصل على مجموع من 2 إلى 12، باستثناء 7، قبل الحصول على مجموع 7. عادةً ما تدفع المكاسب 150 إلى 1.
في عام 2021، بدأت أرى نفس الرهانات المسماة "Diceology" في البندقية.
تحليل
يوضح الجدول التالي تحليلي للرهانات الصغيرة والطويلة، عندما تكون نسبة الفوز 30 إلى 1. تُظهر الخلية اليمنى السفلية ميزة للمنزل بنسبة 18.30%.
صغير وطويل
| حدث | يدفع | احتمال | يعود |
|---|---|---|---|
| يفوز | 30 | 0.026354 | 0.790617 |
| خسارة | -1 | 0.973646 | -0.973646 |
| المجموع | 1.000000 | -0.183029 |
في الماضي، كانت بعض الطاولات تُقدم نسبة ربح ٣٤ إلى ١ على طاولات "الصغيرة والكبيرة". أما هذه الطاولات الأكثر سخاءً، فتتميز بنسبة ربح للكازينو تبلغ ٧٫٧٦٪.
يوضح الجدول التالي تحليلي لرهان الكل، عندما تدفع المكاسب 150 إلى 1. تُظهر الخلية اليمنى السفلية ميزة للمنزل بنسبة 20.61%.
الجميع
| حدث | يدفع | احتمال | يعود |
|---|---|---|---|
| يفوز | 150 | 0.005258 | 0.788655 |
| خسارة | -1 | 0.994742 | -0.994742 |
| المجموع | 1.000000 | -0.206087 |
لقد رأيتُ عوائد أخرى على رهان الكل، بما في ذلك ١٥٥ و١٧٥ إلى ١. تذكر طرح واحد من العوائد لتحويل احتمالات "لواحد" إلى "لواحد". يوضح الجدول التالي هامش الكازينو لجميع العوائد القابلة للقسمة بالتساوي على ٥ من ١٥٠ إلى ١٧٥.
ملخص ميزة المنزل في جميع الرهانات
| يدفع | حافة المنزل |
|---|---|
| 150 | 20.61% |
| 155 | 17.98% |
| 160 | 15.35% |
| 165 | 12.72% |
| 170 | 10.09% |
| 175 | 7.46% |
المنهجية
لقد قمت بتحليل لعبة Bonus Craps بثلاث طرق، على النحو التالي:
- المحاكاة - ربما تكون هذه أسهل طريقة. مع ذلك، بالنسبة لمُحبي الرياضيات المتشددين مثلي، فإن المحاكاة دائمًا ما تكون غير مُرضية فكريًا.
- سلسلة ماركوف - هذه الطريقة مُرهقة وتستغرق وقتًا طويلاً. بالنسبة للصغير والطويل، تتطلب مصفوفة انتقالية ٦×٦، وللجميع ١٢×١٢.
- حساب التكامل - هذه الطريقة سهلةٌ للغاية باستخدام حاسبة التكامل. سأشرحها بمزيدٍ من التفصيل أدناه.
تخيل أنه بدلاً من تحديد الأحداث المهمة برمي النرد، واحدة تلو الأخرى، اعتبرها لحظة زمنية. لنفترض أن الوقت الفاصل بين الأحداث لا يعتمد على الذاكرة، حيث يبلغ متوسطه وحدة زمنية واحدة. بمعنى آخر، يتبع الوقت الفاصل بين الأحداث توزيعًا أُسيًا بمتوسط 1. لن يكون هذا مهمًا عند تقييم الرهان، لأن الأحداث لا تزال تقع واحدة تلو الأخرى.
فيما يلي احتمال عدم ظهور أي إجمالي معين مرة واحدة على الأقل خلال x وحدات من الوقت:
- 2 أو 12: exp(-x/36)
- 3 أو 11: exp(-x/18)
- 4 أو 10: exp(-x/12)
- 5 أو 9: exp(-x/9)
- 6 أو 8: exp(-5x/36)
- 7: exp(-x/6)
لنلقِ نظرة على الرهان الصغير أولًا. احتمالات الرهان الكبير متطابقة تمامًا.
في وحدات زمنية x، احتمالية ظهور الأرقام 2 و3 و4 و5 و6، وعدم ظهور الرقم 7 هي: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6) احتمالية ظهور الرقم 7 في الوقت x، بعد ظهور كل مجموع من 2 إلى 6، هي:
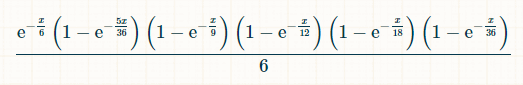
بالنسبة للتكامل، استخدمت حاسبة التكامل هذه.
بما أن الفوز بالرقم 7 ممكن في أي وقت، فإن احتمال الفوز هو تكامل هذا الاحتمال على x من 0 إلى ما لا نهاية. ليس من الضروري أن نعرف ذلك، ولكن التكامل قبل وضع حدود التكامل هو: (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^(-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(- (7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^(-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6.
عند وضع حدود التكامل، تكون الإجابة هي 20049 / 760760 = تقريبًا 0.02635390924864609.
الآن دعونا نلقي نظرة على الرهان الشامل.
في وحدات زمنية x، احتمالية ظهور الأرقام 2، 3، 4، 5، 6، 8، 9، 10، 11، و12، وعدم ظهور الرقم 7 هي: (1-exp(-x/36)) 2 *(1-exp(-x/16)) 2 *(1-exp(-x/12)) 2 *(1-exp(-x/9)) 2 *(1-exp(-5x/36)) 2 *exp(-x/6) احتمالية ظهور الرقم 7 في الوقت x، بعد ظهور كل إجمالي من 2 إلى 6، هي:
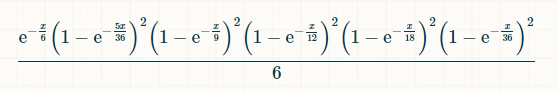
بما أن الفوز بالرقم 7 ممكن في أي وقت، فإن احتمال الفوز هو تكامل هذا الاحتمال على x من 0 إلى ما لا نهاية. ليس من الضروري أن نعرف، ولكن التكامل قبل وضع حدود التكامل هو (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* ه^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e) ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6.
وبوضع حدود التكامل، تكون الإجابة هي 126538525259 / 24067258815600 = 0.0052577040961964420049.



