على هذه الصفحة
ثنائيات مختلفة
مقدمة
"الزوجي المختلف" هو رهان جانبي في لعبة الكرابس، وقد شوهد في كازينو بو ريفاج في بيلوكسي. يُدفع بناءً على عدد الأرقام المزدوجة الفريدة التي يرميها اللاعب قبل أن يصل مجموعها إلى سبعة. جدول الدفع كالتالي:
- 6 أزواج تدفع 100 إلى 1
- 5 أزواج تدفع 15 إلى 1
- 4 أزواج تدفع 8 إلى 1
- 3 أزواج تدفع 4 إلى 1
تحليل
يوضح الجدول أدناه احتمالية ومساهمة جميع النتائج المحتملة في عائد الرهان. تُظهر الخلية اليمنى السفلية نسبة ربح للكازينو تبلغ ٢٧.٩٢٪ (يا للأسف!).
جدول إرجاع الزوجي المختلف
| صنع الزوجي | يدفع | التركيبات | احتمال | يعود |
|---|---|---|---|---|
| 6 | 100 | 1 | 0.001082 | 0.108225 |
| 5 | 15 | 6 | 0.006494 | 0.097403 |
| 4 | 8 | 21 | 0.022727 | 0.181818 |
| 3 | 4 | 56 | 0.060606 | 0.242424 |
| 2 | -1 | 126 | 0.136364 | -0.136364 |
| 1 | -1 | 252 | 0.272727 | -0.272727 |
| 0 | -1 | 462 | 0.500000 | -0.500000 |
| المجموع | 924 | 1.000000 | -0.279221 |
التحليل الجبري
احتمال أي رقم مزدوج هو ١/٣٦. وبالتالي، فإن احتمال أي رقم مزدوج هو ٦/٣٦ = ١/٦. واحتمال أي رقم سبعة هو ١/٦. يمكننا تجاهل جميع الرميات باستثناء الرقمين المزدوج والسباعي. لذا، بافتراض وجود رمية مرتبطة بالرهان، فيما يلي احتمالات تلك الرمية:
- أي ضعف = 1/2
- أي سبعة = 1/2
احتمال أن تكون أول رمية مهمة هي سبعة هو ١/٢. وبالتالي، هناك احتمال صفر للتكرارات.
وإلا، لكان اللاعب قد حصل على نتيجة مزدوجة. يمكننا الآن تجاهل هذه النتيجة المزدوجة مرة أخرى كحدث هام. احتمالية كلا النوعين من الأحداث الهامة هي الآن:
- أي ضعف كبير = 5/11
- أي سبعة = 6/11
احتمال حصول اللاعب على الرقم سبعة في هذه المرحلة، لنتيجة مزدوجة واحدة، هو 6/11. وبالتالي، فإن الاحتمال الإجمالي لنتيجة مزدوجة واحدة هو (1/2)*(6/11) = 3/11 = حوالي 27.27%.
وإلا، لكان اللاعب قد حصل على نرد مزدوج ثانٍ. يمكننا الآن تجاهل رمي نردين مزدوجين مختلفين كحدث هام. احتمالية كلا النوعين من الأحداث الهامة هي الآن:
- أي ضعف كبير = 4/10
- أي سبعة = 6/10
احتمال حصول اللاعب على الرقم سبعة في هذه المرحلة، لرقمين مزدوجين، هو 6/10. وبالتالي، فإن الاحتمال الإجمالي لرقم مزدوج واحد هو (1/2)*(5/11)*(6/10) = 3/22 = حوالي 13.6363636%.
وإلا، لكان اللاعب قد حصل على نرد مزدوج ثالث. يمكننا الآن تجاهل رمي ثلاثة نردات مزدوجة مختلفة كحدث هام. احتمالية كلا النوعين من الأحداث الهامة هي الآن:
- أي ضعف كبير = 3/9
- أي سبعة = 6/9
احتمال حصول اللاعب على الرقم سبعة في هذه المرحلة، لرقمين مزدوجين، هو 6/9. وبالتالي، فإن الاحتمال الإجمالي لرقم مزدوج واحد هو (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = تقريبًا 6.060606%.
وإلا، لكان اللاعب قد حصل على نرد مزدوج رابع. يمكننا الآن تجاهل أربعة نردات مزدوجة مميزة كحدث هام. احتمالية كلا النوعين من الأحداث الهامة هي الآن:
- أي ضعف كبير = 2/8
- أي سبعة = 6/8
احتمال حصول اللاعب على الرقم سبعة في هذه المرحلة، لرقمين مزدوجين، هو 6/8. وبالتالي، فإن الاحتمال الإجمالي لرقم مزدوج واحد هو (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = تقريبًا 2.272727%.
وإلا، لكان اللاعب قد حصل على النرد المزدوج الخامس. يمكننا الآن تجاهل خمسة نردات مزدوجة مميزة كحدث مهم. احتمالية كلا النوعين من الأحداث المهمة هي الآن:
- أي ضعف كبير = 1/7
- أي سبعة = 6/7
احتمال حصول اللاعب على الرقم سبعة في هذه المرحلة، لرقمين مزدوجين، هو 6/7. وبالتالي، فإن الاحتمال الإجمالي لرقم مزدوج واحد هو (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = تقريبًا 0.649351%.
وإلا، لكان اللاعب قد حصل على آخر رقم مزدوج متبقٍ. احتمال ذلك هو (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = تقريبًا 0.108225%.
يمكننا الآن جمع كل ذلك في جدول الإرجاع أعلاه. عدد التركيبات هو ٩٢٤.
تحليل حساب التفاضل والتكامل
تخيل أنه بدلاً من تحديد الأحداث المهمة برمي النرد، واحدة تلو الأخرى، اعتبرها لحظة زمنية. لنفترض أن الوقت الفاصل بين الأحداث لا يعتمد على الذاكرة، حيث يبلغ متوسطه وحدة زمنية واحدة. بمعنى آخر، يتبع الوقت الفاصل بين الأحداث توزيعًا أُسيًا بمتوسط 1. لن يكون هذا مهمًا عند تقييم الرهان، لأن الحدث لا يزال يقع واحدًا تلو الآخر.
يتبع الزمن الفاصل بين تكرارين محددين توزيعًا أُسيًا بمتوسط ١٢. والسبب في ذلك هو أنه في حال وقوع حدث ذي دلالة إحصائية، فإن احتمال وقوع هذا التكرار المحدد هو ١/١٢. لذا، فإن احتمال عدم حدوث تكرار محدد خلال x وحدة زمنية هو exp(-x/12). وبالتالي، فإن احتمال حدوثه هو ١-exp(-x/12).
ليكن x عدد الوحدات الزمنية منذ بدء الرهان. احتمال حدوث كل ضعف وعدم حدوث سبعة هو (1-exp(-x/12)) 6 × exp(-x/2).
ولإغلاق ذلك برمي الرقم 7 في الوقت x، اضرب ذلك في 1/2، وهو احتمال الحصول على الرقم 7، للحصول على احتمال الفوز في الوقت x بالضبط وهو (1/2) ×(1-exp(-x/12)) 6 × exp(-x/2)
لإيجاد احتمالية الفوز بالرهان على مدار الوقت، قم بتكامل من 1 إلى ما لا نهاية:
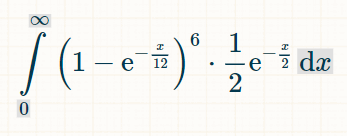
لدمج ذلك، أنصح باستخدام حاسبة التكامل هذه. في حقل التكامل، اكتب "(1-exp(-x/12))^6*(1/2)*exp(-x/2)." لحدود التكامل، ضمن الخيارات، ضع 0 و∞. ثم انقر على "انتقال"."سيعطيك التكامل أدناه:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40) *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
مع ذلك، لسنا بحاجة لإدخال 0 في ذلك. تُعطي الآلة الحاسبة الإجابة كالتالي: ١/٩٢٤ = تقريبًا ٠٫٠٠١٠٨٢٢٥١٠٨٢٢٥١٠٨٢.
هذا هو التكامل لخمسة أعداد ثنائية مختلفة. سبب وجود العدد 6 هو وجود ستة أعداد ثنائية محتملة لم تُصنع:
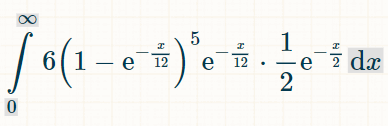
وهنا احتمال الفوز خلال x وحدات من الزمن:
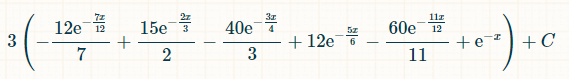
إذا وضعنا حدود التكامل من 0 إلى ما لا نهاية، فإن احتمال الحصول على خمسة أرقام مزدوجة مميزة بالضبط هو 1/154.
هذا هو التكامل لأربعة أعداد ثنائية مختلفة. سبب العدد ١٥ هو وجود ٦!/(٤!*٢!) = ١٥ تركيبة ممكنة لأربعة من أصل ستة أعداد ثنائية تم تكوينها:
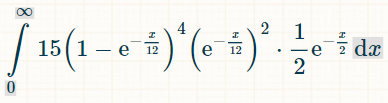
وهنا احتمال الفوز خلال x وحدات من الزمن:
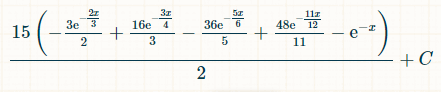
إذا وضعنا حدود التكامل من 0 إلى ما لا نهاية، فإن احتمال الحصول على أربعة أرقام مزدوجة مميزة بالضبط هو 1/44.
هذا هو التكامل لثلاثة أعداد مزدوجة مميزة. سبب وجود العدد ٢٠ هو وجود ٦!/(٣!*٣!) = ٢٠ تركيبة ممكنة لثلاثة من أصل ستة أعداد مزدوجة تم تكوينها:
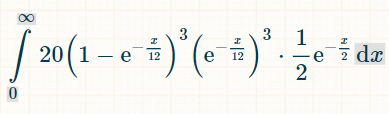
وهنا احتمال الفوز خلال x وحدات من الزمن:
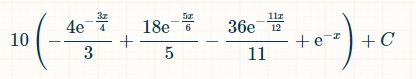
إذا وضعنا حدود التكامل من 0 إلى ما لا نهاية، فإن احتمال الحصول على ثلاثة أرقام مزدوجة مميزة بالضبط هو 2/33.



