WOO logo

يوصي المعالج

على هذه الصفحة

رهان النار

مقدمة

رهان النار رهان جانبي شائع في لعبة الكرابس، يُدفع بناءً على عدد النقاط الفريدة التي يحققها اللاعب ويفوز بها. أعرف ثلاثة جداول دفع، كما يلي. تظهر ميزة الكازينو لكل منها في الصف السفلي من الجدول. جدول الدفع 1 هو الأكثر شيوعًا. تُحسب قيمة الدفع على أساس "إلى واحد". أي قيمة سالبة تعني خسارة.

جداول دفع الرهان على النار

النقاط التي تم تحقيقها جدول الأجور أ جدول الرواتب ب جدول الرواتب ج
6 999 عام 2000 299
5 249 200 149
4 24 10 29
3 -1 -1 6
2 -1 -1 -1
1 -1 -1 -1
0 -1 -1 -1
حافة المنزل 20.76% 24.86% 20.73%

فيما يلي تحليلي لجدول الدفع أ. تُظهر الخلية الموجودة في الجزء السفلي الأيمن ميزة منزلية تبلغ 20.76%.

رهان النار - جدول الدفع أ

النقاط التي تم تحقيقها يدفع احتمال يعود
0 -1 0.593939 -0.593939
1 -1 0.260750 -0.26075
2 -1 0.101275 -0.101275
3 -1 0.033434 -0.033434
4 24 0.008798 0.211156
5 249 0.001640 0.408343
6 999 0.000162 0.162272
المجموع 1 -0.207628

فيما يلي تحليلي لجدول الدفع B. تُظهر الخلية اليمنى السفلية ميزة منزلية تبلغ 24.86%.

رهان النار - جدول الدفع ب

النقاط التي تم تحقيقها يدفع احتمال يعود
0 -1 0.593939 -0.593939
1 -1 0.260750 -0.26075
2 -1 0.101275 -0.101275
3 -1 0.033434 -0.033434
4 10 0.008798 0.087982
5 200 0.001640 0.327987
6 عام 2000 0.000162 0.324869
المجموع 1 -0.248562

فيما يلي تحليلي لجدول الرواتب C. تُظهر الخلية اليمنى السفلية ميزة منزلية تبلغ 20.73%.

رهان النار - جدول الدفع ج

النقاط التي تم تحقيقها يدفع احتمال يعود
0 -1 0.593939 -0.593939
1 -1 0.260750 -0.26075
2 -1 0.101275 -0.101275
3 6 0.033434 0.200605
4 29 0.008798 0.255147
5 149 0.001640 0.244350
6 299 0.000162 0.048568
المجموع 1 -0.207295

يوضح الجدول التالي احتمالات الحصول على نتيجة من 0 إلى 6 نقاط، مع أكبر عدد ممكن من الأرقام المهمة التي يستطيع Excel التعامل معها.

احتمالات الرهان على النار

النقاط التي تم تحقيقها احتمال
0 0.593939393939394
1 0.260750492003903
2 0.101275355549231
3 0.0334342121788456
4 0.00879817844040312
5 0.00163993313895325
6 0.000162434749269826

نردين

كثيرًا ما يُسألني عن كيفية حساب الاحتمالات المذكورة أعلاه. إنها مسألة رياضية معقدة. فيما يلي، أدرج طرقًا لحل احتمالات الحصول على أي عدد من النقاط من ٠ إلى ٦.

محاكاة عشوائية

المحاكاة العشوائية هي أسهل طريقة لتحليل رهان النار. وبفضل سرعة أجهزة الكمبيوتر الحديثة، فهي دقيقة للغاية. لن يسعى سوى أكثر الرياضيين صرامة (مثلي) إلى إيجاد حل دقيق. يوضح الجدول التالي نتائج محاكاة لما يقرب من 40 مليار رهان نار تم حلها مقابل جدول الدفع "أ". تُظهر الخلية السفلية اليمنى ميزة للكازينو بنسبة 20.7531%. تبلغ ميزة الكازينو الفعلية 20.7628%، لذا كانت دقة المحاكاة 0.01% من العائد.

محاكاة رهان النار

النقاط التي تم تحقيقها يدفع انتصارات احتمال يعود
6 999 6,452,452 0.000162 0.162257
5 249 65,165,019 0.001640 0.408438
4 24 349,553,690 0.008799 0.211173
3 -1 1,328,267,592 0.033435 -0.033435
2 -1 4,023,371,732 0.101275 -0.101275
1 -1 10,358,742,102 0.260747 -0.260747
0 -1 23,595,605,529 0.593941 -0.593941
المجموع 39,727,158,116 1.000000 -0.207531

سلسلة ماركوف

إحدى طرق حساب احتمالات رهان النار بدقة هي استخدام سلسلة ماركوف. هذا يعني حساب احتمالية إكمال أي عدد مستقبلي من النقاط، مع الأخذ في الاعتبار أيًا من الحالات الـ 64 المحتملة للنقاط المكتملة بالفعل. تكون العملية الحسابية سهلة نسبيًا في النهاية، حيث لا تحتاج إلا إلى نقطة واحدة لإكمال جميع الحالات الست. ثم عد إلى حالة البداية للرمية الأولى.

تُمثَّل هذه الحالة الأولى بالصف الأول في الجدول، دون احتساب عناوين الأعمدة. وتُظهر الاحتمالات الموضحة أعلاه لإكمال أي عدد من النقاط من ٠ إلى ٦.

سلسلة فاير بيت ماركوف

نقاط
بالفعل
صنع		 احتمال
0 نقطة		 احتمال
1 نقطة		 احتمال
نقطتين		 احتمال
3 نقاط		 احتمال
4 نقاط		 احتمال
5 نقاط		 احتمال
6 نقاط
لا أحد 0.593939 0.260750 0.101275 0.033434 0.008798 0.001640 0.000162
10 0.000000 0.619763 0.256759 0.091331 0.026183 0.005375 0.000589
9 0.000000 0.636364 0.252138 0.084540 0.022402 0.004153 0.000404
9,10 0.000000 0.000000 0.666100 0.244772 0.072316 0.015152 0.001660
8 0.000000 0.656067 0.244255 0.076831 0.019163 0.003370 0.000314
8,10 0.000000 0.000000 0.687719 0.234612 0.063990 0.012405 0.001274
8,9 0.000000 0.000000 0.708220 0.225365 0.055933 0.009618 0.000864
8،9،10 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
6 0.000000 0.656067 0.244255 0.076831 0.019163 0.003370 0.000314
6,10 0.000000 0.000000 0.687719 0.234612 0.063990 0.012405 0.001274
6,9 0.000000 0.000000 0.708220 0.225365 0.055933 0.009618 0.000864
6،9،10 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
6,8 0.000000 0.000000 0.732710 0.210728 0.048135 0.007762 0.000665
6،8،10 0.000000 0.000000 0.000000 0.772414 0.190903 0.033563 0.003120
6،8،9 0.000000 0.000000 0.000000 0.798371 0.173323 0.026215 0.002091
6،8،9،10 0.000000 0.000000 0.000000 0.000000 0.845739 0.142050 0.012211
5 0.000000 0.636364 0.252138 0.084540 0.022402 0.004153 0.000404
5,10 0.000000 0.000000 0.666100 0.244772 0.072316 0.015152 0.001660
5,9 0.000000 0.000000 0.685315 0.237358 0.064328 0.011875 0.001124
5،9،10 0.000000 0.000000 0.000000 0.719927 0.224997 0.049645 0.005432
5,8 0.000000 0.000000 0.708220 0.225365 0.055933 0.009618 0.000864
5،8،10 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
5،8،9 0.000000 0.000000 0.000000 0.769382 0.195368 0.032496 0.002754
5،8،9،10 0.000000 0.000000 0.000000 0.000000 0.813278 0.170376 0.016346
5,6 0.000000 0.000000 0.708220 0.225365 0.055933 0.009618 0.000864
5،6،10 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
5،6،9 0.000000 0.000000 0.000000 0.769382 0.195368 0.032496 0.002754
5،6،9،10 0.000000 0.000000 0.000000 0.000000 0.813278 0.170376 0.016346
5،6،8 0.000000 0.000000 0.000000 0.798371 0.173323 0.026215 0.002091
5،6،8،10 0.000000 0.000000 0.000000 0.000000 0.845739 0.142050 0.012211
5،6،8،9 0.000000 0.000000 0.000000 0.000000 0.876957 0.114977 0.008066
5،6،8،9،10 0.000000 0.000000 0.000000 0.000000 0.000000 0.934446 0.065554
4 0.000000 0.619763 0.256759 0.091331 0.026183 0.005375 0.000589
4,10 0.000000 0.000000 0.647934 0.250930 0.079930 0.018752 0.002454
4,9 0.000000 0.000000 0.666100 0.244772 0.072316 0.015152 0.001660
4،9،10 0.000000 0.000000 0.000000 0.698752 0.234682 0.058434 0.008131
4,8 0.000000 0.000000 0.687719 0.234612 0.063990 0.012405 0.001274
4،8،10 0.000000 0.000000 0.000000 0.722581 0.221643 0.049624 0.006153
4،8،9 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
4،8،9،10 0.000000 0.000000 0.000000 0.000000 0.786359 0.188851 0.024790
4,6 0.000000 0.000000 0.687719 0.234612 0.063990 0.012405 0.001274
4،6،10 0.000000 0.000000 0.000000 0.722581 0.221643 0.049624 0.006153
4،6،9 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
4،6،9،10 0.000000 0.000000 0.000000 0.000000 0.786359 0.188851 0.024790
4،6،8 0.000000 0.000000 0.000000 0.772414 0.190903 0.033563 0.003120
4،6،8،10 0.000000 0.000000 0.000000 0.000000 0.816667 0.164832 0.018502
4،6،8،9 0.000000 0.000000 0.000000 0.000000 0.845739 0.142050 0.012211
4،6،8،9،10 0.000000 0.000000 0.000000 0.000000 0.000000 0.899083 0.100917
4,5 0.000000 0.000000 0.666100 0.244772 0.072316 0.015152 0.001660
4،5،10 0.000000 0.000000 0.000000 0.698752 0.234682 0.058434 0.008131
4،5،9 0.000000 0.000000 0.000000 0.719927 0.224997 0.049645 0.005432
4،5،9،10 0.000000 0.000000 0.000000 0.000000 0.758221 0.208531 0.033248
4،5،8 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
4،5،8،10 0.000000 0.000000 0.000000 0.000000 0.786359 0.188851 0.024790
4،5،8،9 0.000000 0.000000 0.000000 0.000000 0.813278 0.170376 0.016346
4،5،8،9،10 0.000000 0.000000 0.000000 0.000000 0.000000 0.862486 0.137514
4،5،6 0.000000 0.000000 0.000000 0.745247 0.209635 0.041004 0.004114
4،5،6،10 0.000000 0.000000 0.000000 0.000000 0.786359 0.188851 0.024790
4،5،6،9 0.000000 0.000000 0.000000 0.000000 0.813278 0.170376 0.016346
4،5،6،9،10 0.000000 0.000000 0.000000 0.000000 0.000000 0.862486 0.137514
4،5،6،8 0.000000 0.000000 0.000000 0.000000 0.845739 0.142050 0.012211
4،5،6،8،10 0.000000 0.000000 0.000000 0.000000 0.000000 0.899083 0.100917
4،5،6،8،9 0.000000 0.000000 0.000000 0.000000 0.000000 0.934446 0.065554
4،5،6،8،9،10 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000

إذا كنت تخطط لمحاولة إعادة تمثيل عملي، فإليك بعض النصائح للانتقال من حالة إلى أخرى. ابدأ بالحالات القريبة من النهاية، والتي أحرز فيها الرامي خمس نقاط. على سبيل المثال، إذا احتاج الرامي إلى 4 فقط، فقد تحدث ثلاثة أمور: (1) يُحقق الرامي 4 ويسجلها، (2) يُحقق الرامي نقطة سبق أن أحرزها، (3) يُخرج سبعة. احتمال (1) هو (3/24)*(1/3) = 1/24 = 0.041667. احتمال (2) هو (4/24)*(2/5) + (5/24)*(5/11) + (5/24)*(5/11) + (4/24)*(2/5) + (3/24)*(1/3) = 0.364394. احتمال (3) هو 1- 0.041667 - 0.364394 = 0.593939. في النهاية، سيقع الحدث (1) أو (3). احتمال وقوع (1) قبل (3) هو 0.041667/(0.041667 + 0.593939) = 0.065554. عد إلى نقطة البداية بشكل متكرر. سيكون هذا إما مستهلكًا للوقت، أو مكررًا، أو يمكنك القيام به تلقائيًا في جدول بيانات.

حساب التفاضل والتكامل

الخطوة الأولى في هذه الطريقة هي حساب احتمالية جميع النتائج السبع المحتملة لرهان خط المرور بعد تحديد نقطة. يمكننا تجاهل احتمالية فوز اللاعب أو خسارته فورًا عند رمية الخروج (الخروج)، وهي 1/3، لأن هذه الأحداث ليست ذات أهمية بالنسبة لرهان النار. لذا، تعتمد الرمية الأولى على 24 تركيبة محتملة، بدلًا من 36.

  • نقطة من 4 نقاط تم الحصول عليها وربحها = (3/24) × (3/9) = 1/24 = تقريبًا 4.17%
  • نقاط 5 التي تم الحصول عليها وربحها = (4/24) × (4/10) = 1/15 = تقريبًا 6.67%
  • نقاط الـ 6 المكتسبة والمربحة = (5/24) × (5/11) = 25/264 = تقريبًا 9.47%
  • نقاط 8 التي تم الحصول عليها وربحها = (5/24) × (5/11) = 25/264 = تقريبًا 9.47%
  • نقاط 9 التي تم الحصول عليها وربحها = (4/24) × (4/10) = 1/15 = تقريبًا 6.67%
  • نقطة 10 التي تم الحصول عليها وربحها = (3/24) × (3/9) = 1/24 = تقريبًا 4.17%
  • أي نقطة تم الحصول عليها و7 خارج = 2×((3/24) × (6/9))+ 2× ((4/24) × (6/10)) + 2×((5/24) × (6/11)) = 98/165 = تقريبًا 59.39%

يرجى ملاحظة أن مجموع هذه الاحتمالات يساوي 1.

بعد ذلك، بدلًا من تحديد رهان النار برمي حجري نرد، رمية تلو الأخرى، خُذ في الاعتبار أن الوقت بين الأحداث يحدث عشوائيًا، بحيث يتبع الوقت بين الأحداث توزيعًا أُسيًا بمتوسط وحدة زمنية واحدة. إذا وقع حدث ما، فسيتبع هذا الحدث احتمالات لعبة الكرابس التي حسبناها للتو.

على سبيل المثال، احتمال الفوز بنقطة -٤ هو ١/٢٤. وبالتالي، فإن متوسط الوقت بين الفوز بنقطة -٤ هو ٢٤ وحدة. واحتمال عدم الفوز بنقطة -١٠ خلال x وحدات زمنية هو exp(-x/٢٤). وللحصول على النتيجة، فإن احتمال فوز واحد على الأقل بنقطة -١٠ خلال x وحدات زمنية هو ١-exp(-x/٢٤).

للتحكيم في رهان النار، لا يهم كم من الوقت انقضى بين الأحداث، بل المهم هو طبيعة الأحداث. لذا، يمكننا حساب إجمالي الوقت للفائز في الرهان كما يلي:

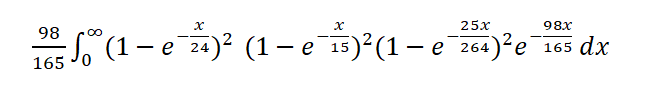
دعوني أشرح معنى هذا التكامل. إنه احتمال أن يكون هناك فوز واحد على الأقل لكل نقطة بعد x وحدة زمنية، باستثناء 7. بما أن احتمال الفوز بنقطة -4 ونقطة -10 متساوٍ، يمكننا تربيع احتمال الفوز بنقطة -4. كما هو الحال بالنسبة للنقطتين 5 و9، وكذلك 6 و8. أخيرًا، نضرب الناتج في 98/165، وهو احتمال الفوز بسبع نقاط، لإغلاق الرهان. إذا لم نفعل ذلك، فقد يحصل اللاعب على مكافأة مقابل فوزين متداخلين.

سيكون دمج هذا يدويًا مُرهقًا جدًا وعرضةً للأخطاء. لحسن الحظ، توجد آلات حاسبة للتكامل . لاستخدام الآلة الحاسبة في هذه المسألة، انقر على الرابط، ثم اكتب ما يلي في مربع النص بالأعلى: (1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25x/264))^2*exp(-98x/165)/(165/98). ثم انقر على الخيارات، واضبط الحد الأدنى على 0 والحد الأقصى على ما لا نهاية. ثم انقر على "انتقال".

قبل النظر في حدود التكامل، الإجابة هي (98*(-(165*e^(-(98*x)/165))/98+(2640*e^(-(839*x)/1320))/839+(330*e^(-(109*x)/165))/109-(220*e^(-(149*x)/220))/149+(880*e^(-(303*x)/440))/303-(1760*e^(-(309*x)/440))/309-(11* ه^(-(8*x)/11))/8-(1320*e^(-(241*x)/330))/241+(1320*e^(-(491*x)/660))/491-(5280*e^(-(99) 7*x)/1320))/997+(528*e^(-(203*x)/264))/203+(2640*e^(-(1019*x)/1320))/1019-(60*e^(-(47*x) )/60))/47+(2640*e^(-(263*x)/330))/263-(132*e^(-(107*x)/132))/107+(528*e^(-(217*x)/264) )/217+(80*e^(-(33*x)/40))/33-(1760*e^(-(369*x)/440))/369+(40*e^(-(17*x)/20))/17-(88*e^( -(19*x)/22))/19-(15*e^(-(13*x)/15))/13-(480*e^(-(107*x)/120))/107+(528*e^(-(239*x)/264) )/239-(12*e^(-(11*x)/12))/11+(15*e^(-(14*x)/15))/7+(48*e^(-(23*x)/24))/23-e^(-x)))/165.

لحسن الحظ، تسمح هذه الآلة الحاسبة بحدود التكامل وتقدم الحل على النحو التالي 3700403899126040038831518494284887738125 / 22780863797678919004236184338193605974839452، وهو ما يعادل تقريبًا 0.0001624347492698264.

بالطبع، هذا مجرد احتمالية الحصول على جميع النقاط الست، ولكن يمكن استخدام نفس المنطق لإيجاد احتمالية أي عدد من النقاط. سأترك هذا للقارئ كتمرين.

الروابط الخارجية

الشكر والتقدير

أود أن أشكر عضو منتدى Wizard of Vegas، Ace2، على نصيحته المتواصلة بشأن حل احتمالية رهان النار باستخدام التكامل.

كتبه: Michael Shackleford