على هذه الصفحة
سباق الآس
مقدمة
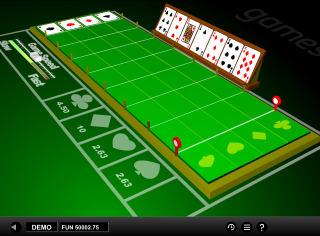
سباق الآس هي لعبة سباق بسيطة على طراز ديربي من تطوير 1x2 Gaming . الفكرة هي أن اللاعب يراهن على نوع معين. ثم تُسحب بطاقات عشوائية من مجموعة أوراق اللعب حتى تظهر إحدى هذه الأنواع ثماني مرات، وعندها تكون هي الفائزة. يمكن للاعب المراهنة قبل أو بعد توزيع سبع بطاقات أولية.
تتراوح العائدات من 50.71% إلى 97.26%، اعتمادًا على نوع الرهان الذي تقوم به، لذا اختر رهانك بعناية.
قواعد
- يتم لعب اللعبة باستخدام مجموعة من 48 بطاقة، باستخدام جميع البطاقات باستثناء الآسات.
- سيتم وضع الآسات الأربعة التي تم إزالتها على خط البداية للملعب.
- يمكن للاعب المراهنة إما بـ "Ante Post" أو "With Form".
- إذا اختار اللاعب "Ante Post"، فسيراهن في هذه المرحلة على إحدى المجموعات الأربع. يُدفع لكل رهان 3.75 لكل رهان في حال فوزه. بعد أن يُجري اللاعب رهانه، ستظهر أول سبع بطاقات في المجموعة.
- إذا اختار اللاعب "مع الشكل"، فسيتم الكشف عن أول سبع بطاقات في المجموعة. ثم تُعدّل الاحتمالات بناءً على عدد البطاقات المُزالة من كل نوع. ويمكن للاعب بعد ذلك المراهنة على أي نوع.
- يبدو أن اللعبة تلغي المواقف التي يتم فيها إزالة خمسة أو أكثر من نفس النوع، لأنه سيكون من المستحيل حينئذٍ أن يفوز هذا النوع، لأنه لن يتبقى ما يكفي من هذا النوع للوصول إلى خط النهاية.
- بعد ذلك، سيبدأ السباق مع البطاقات الـ41 المتبقية، والتي سيتم الكشف عنها واحدة تلو الأخرى.
- مع الكشف عن كل بطاقة، فإن الآس من نفس نوع تلك البطاقة سوف يتقدم موضعًا واحدًا.
- أول آس يتقدم ثماني مرات سيفوز، كما ستفوز الرهانات على نوع ذلك الآس.
إذا اختار اللاعب المراهنة "بشكل صحيح"، فسيتم الكشف عن أول سبع بطاقات في المجموعة قبل السباق. هذا بالطبع يُغيّر الاحتمالات. كلما زاد عدد البطاقات المُزالة من أي نوع، انخفضت فرص فوز ذلك النوع، وبالتالي زادت قيمة الرهان الفائز. لاحظتُ أنه لا يتم إزالة خمس بطاقات أو أكثر من نفس النوع، لأن ذلك يعني أن فرصة الفوز معدومة. هذا يترك سبع طرق أخرى لتوزيع الأنواع على البطاقات السبع الأولى. يوضح الجدول التالي هذه الطرق السبع لإزالة سبع بطاقات، وقيمة كل نوع. جميع المكاسب تُحسب على أساس "لواحد"، أي أن اللاعب لا يسترد رهانه الأصلي في حال الفوز.
جدول دفع سباق الآس
| البدلة 1 تمت الإزالة | البدلة 2 تمت الإزالة | البدلة 3 تمت الإزالة | البدلة 4 تمت الإزالة | البدلة 1 يدفع | البدلة 2 يدفع | البدلة 3 يدفع | البدلة 4 يدفع |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 2.05 | 2.05 | 11 | 34 |
| 0 | 1 | 2 | 4 | 1.83 | 3 | 5.5 | 34 |
| 0 | 1 | 3 | 3 | 1.8 | 2.87 | 11 | 11 |
| 0 | 2 | 2 | 3 | 1.61 | 5.2 | 5.2 | 12 |
| 1 | 2 | 2 | 2 | 2.5 | 4.33 | 4.33 | 4.33 |
| 1 | 1 | 2 | 3 | 2.63 | 2.63 | 4.5 | 10 |
| 1 | 1 | 1 | 4 | 2.87 | 2.87 | 2.87 | 26 |
لنلقِ نظرة على هذا المثال. في أول سبع بطاقات على اللوحة على طول المسار، توجد بطاقة بستوني، وبطاقة قلب، وثلاث بطاقات ألماس، وبطاقة سباتي. يتبع هذا نمط توزيع البطاقات "1-1-2-3" الموضح في الجدول أعلاه. لذا، فإن كلا النوعين بعد إزالة بطاقة واحدة (البستوني والقلوب) يدفع 2.63، والبطاقة بعد إزالة بطاقتين (السباعي) تدفع 4.5، والبطاقة بعد إزالة ثلاث بطاقات (الألماس) تدفع 10.
تحليل
عندما يلعب اللاعب قبل أن يرى البطاقات السبع الأولى، فإن احتمال فوزه هو ٢٥٪. وبنسبة ٣.٧٥ لكل ١، فإن العائد المتوقع هو ٩٣.٧٥٪.
يوضح الجدول التالي احتمال الفوز، ونسب الفوز، والعائد المتوقع عند وقوع البطاقات السبع الأولية ضمن توزيع 0-0-3-4. يُرجى ملاحظة أن أفضل الاحتمالات تكون عندما يكون هناك صفر مفقود في أحد أنواع البطاقات، عند ربح 2.05 وعائد 94.17%.
توزيع البدلة 0-0-3-4
| تمت الإزالة من البدلة | يدفع | احتمال يفوز | مُتوقع يعود |
|---|---|---|---|
| 0 | 2.05 | 0.459382 | 0.941733 |
| 0 | 2.05 | 0.459382 | 0.941733 |
| 3 | 11.00 | 0.064797 | 0.712767 |
| 4 | 34.00 | 0.016440 | 0.558960 |
يوضح الجدول التالي احتمال الفوز، ونسب الفوز، والعائد المتوقع عند وقوع البطاقات السبع الأولية ضمن توزيع ألوان 0-1-2-4. يُرجى ملاحظة أن أفضل الاحتمالات تكون عندما تكون هناك بطاقة مفقودة من نفس النوع، مع عائد 3 ونسبة عائد 93.68%.
توزيع البدلات 0-1-2-4
| تمت الإزالة من البدلة | يدفع | احتمال يفوز | مُتوقع يعود |
|---|---|---|---|
| 0 | 1.83 | 0.500181 | 0.915331 |
| 1 | 3.00 | 0.312262 | 0.936786 |
| 2 | 5.50 | 0.169121 | 0.930166 |
| 4 | 34.00 | 0.018435 | 0.626790 |
يوضح الجدول التالي احتمال الفوز، ونسب الفوز، والعائد المتوقع عند وقوع البطاقات السبع الأولية ضمن توزيع ألوان 0-1-3-3. يُرجى ملاحظة أن أفضل الاحتمالات تكون عندما يكون هناك صفر مفقود في أحد الألوان، بنسبة دفع 1.8 وعائد 93.86%.
توزيع البدلات 0-1-3-3
| تمت الإزالة من البدلة | يدفع | احتمال يفوز | مُتوقع يعود |
|---|---|---|---|
| 0 | 1.80 | 0.521466 | 0.938639 |
| 1 | 2.87 | 0.326610 | 0.937371 |
| 3 | 11.00 | 0.075962 | 0.835582 |
| 3 | 11.00 | 0.075962 | 0.835582 |
يوضح الجدول التالي احتمال الفوز، ونسب الفوز، والعائد المتوقع عند ظهور البطاقات السبع الأولية بتوزيع ألوان 0-2-2-3. يُرجى ملاحظة أن أفضل الاحتمالات تكون عند وجود بطاقتين مفقودتين من نفس النوع، بنسبة ربح 5.2 وعائد 97.26%.
توزيع البدلات 0-2-2-3
| تمت الإزالة من البدلة | يدفع | احتمال يفوز | مُتوقع يعود |
|---|---|---|---|
| 0 | 1.61 | 0.545564 | 0.878358 |
| 2 | 5.20 | 0.187042 | 0.972618 |
| 2 | 5.20 | 0.187042 | 0.972618 |
| 3 | 12.00 | 0.080351 | 0.964212 |
يوضح الجدول التالي احتمال الفوز، ونسب الفوز، والعائد المتوقع عند ظهور البطاقات السبع الأولية بتوزيع 1-2-2-2. يُرجى ملاحظة أن أفضل الاحتمالات تكون عند وجود بطاقة مفقودة من نفس النوع، بنسبة ربح 2.5 وعائد 94.41%.
توزيع البدلة 1-2-2-2
| تمت الإزالة من البدلة | يدفع | احتمال يفوز | مُتوقع يعود |
|---|---|---|---|
| 1 | 2.50 | 0.377634 | 0.944085 |
| 2 | 4.33 | 0.207455 | 0.898280 |
| 2 | 4.33 | 0.207455 | 0.898280 |
| 2 | 4.33 | 0.207455 | 0.898280 |
يوضح الجدول التالي احتمال الفوز، ونسب الفوز، والعائد المتوقع عند ظهور البطاقات السبعة الأولية بتوزيع 1-1-2-3. يُرجى ملاحظة أن أفضل الاحتمالات تكون عند وجود بطاقة مفقودة من نفس النوع بنسبة ربح 2.63 وعائد 94.49%.
توزيع البدلات 1-1-2-3
| تمت الإزالة من البدلة | يدفع | احتمال يفوز | مُتوقع يعود |
|---|---|---|---|
| 1 | 2.63 | 0.359279 | 0.944904 |
| 1 | 2.63 | 0.359279 | 0.944904 |
| 2 | 4.50 | 0.196660 | 0.884970 |
| 3 | 10.00 | 0.084783 | 0.847830 |
يوضح الجدول التالي احتمال الفوز، ونسب الفوز، والعائد المتوقع عند ظهور البطاقات السبعة الأولية بتوزيع 1-1-1-4. يُرجى ملاحظة أن أفضل الاحتمالات تكون عند وجود بطاقة مفقودة من نفس النوع، بنسبة ربح 2.87 وعائد 93.80%.
توزيع البدلات 1-1-1-4
| تمت الإزالة من البدلة | يدفع | احتمال يفوز | مُتوقع يعود |
|---|---|---|---|
| 1 | 2.87 | 0.326832 | 0.938008 |
| 1 | 2.87 | 0.326832 | 0.938008 |
| 1 | 2.87 | 0.326832 | 0.938008 |
| 4 | 26.00 | 0.019503 | 0.507078 |