على هذه الصفحة
ملحق سيك بو
على هذه الصفحة
مقدمة

الصورة مأخوذة من كتاب قواعد فندق/كازينو كلاريدج.
مكافآت سيك بو عبر الإنترنت عرض الكل
- قليل :
لولا استثناء الثلاثية، لما كان لهذا الرهان أي ميزة للكازينو. احتمالية الحصول على ثلاثية 1، 2، أو 3 هي 3/216. احتمالية أي مجموع بين 3 و10 هي 1/2، أو 108/216. لذا، فإن احتمالية الفوز بثلاثية هي 108/216 - 3/216 = 105/216. وبالتالي، تكون ميزة اللاعب (105/216)*(+1) + (111/216)*(-1) = -6/216 = ~-2.78%.
- مرتفع : انظر منخفض.
- رقم محدد :
احتمال ظهور صفر لرقم معين هو (5/6) 3 = 125/216.
احتمال الحصول على رقم معين هو 3*(1/6) 1 *(5/6) 2 = 75/216.
احتمال الحصول على رقمين محددين هو 3*(1/6) 2 *(5/6) 1 = 15/216.
احتمال الحصول على ثلاثة من عدد معين هو (1/6) 3 = 1/216.
وبالتالي فإن ميزة اللاعب هي (125/216)*(-1) + (75/216)*(+1)+ (15/216)*(+2) + (1/216)*(+3) = -17/216 =~-7.780%. - المجموع 4 :
هناك ثلاث طرق لرمي 4 نردات: (1+1+2، 1+2+1، 2+1+1). بالتالي، تكون نسبة ربح اللاعب 3/216*(+60) + (213/216)*(-1) = -33/216 = -15.278%.
- المجموع 5 :
هناك ست طرق لرمي ٥ أوراق: (١+١+٣، ١+٣+١، ٣+١+١، ١+٢+٢، ٢+١+٢، ٢+٢+١). وبالتالي، تكون نسبة ربح اللاعب ٦/٢١٦*(+٣٠) + (٢١٠/٢١٦)*(-١) =-٣٠/٢١٦ = -١٣.٨٨٩٪.
- المجموع 6 :
هناك ١٠ طرق لرمي ٦: (١+١+٤، ١+٤+١، ٤+١+١، ١+٢+٣، ١+٣+٢، ٢+١+٣، ٢+٣+١، ٣+١+٢، ٣+٢+١، ٢+٢+٢). وبالتالي، تكون ميزة اللاعب ١٠/٢١٦*(+١٧) + (٢٠٦/٢١٦)*(-١) = -٣٦/٢١٦ = -١٦٫٦٦٧٪.
- المجموع 7 :
هناك 15 طريقة للحصول على 7: (1+1+5، 1+5+1، 5+1+1، 1+2+4، 1+4+2، 2+1+4، 2+4+1، 4+1+2، 4+2+1، 1+3+3، 3+1+3، 3+3+1، 2+2+3، 2+3+2، 3+2+2). وبالتالي فإن ميزة اللاعب هي 15/216*(+12) + (201/216)*(-1) =-21/216 = -9.722%.
- المجموع 8 :
هناك ٢١ طريقة لرمي ٨ نردات: (١-٦-٦ * ٣ طرق، ١-٢-٥ * ٦ طرق، ١-٣-٤ * ٦ طرق، ٢-٢-٤ * ٣ طرق، ٢-٣-٣ * ٣ طرق). وبالتالي، تكون نسبة ربح اللاعب ٢١/٢١٦ * (+٨) + (١٩٥/٢١٦) * (-١) = -٢٧/٢١٦ = -١٢٫٥٠٠٪.
- المجموع 9 :
هناك ٢٥ طريقة لرمي ٩ نردات: (١-٢-٦ * ٦ طرق، ١-٣-٥ * ٦ طرق، ١-٤-٤ * ٣ طرق، ٢-٢-٥ * ٣ طرق، ٢-٣-٤ * ٦ طرق، ٣-٣-٣ * طريقة واحدة). وبالتالي، تكون ميزة اللاعب ٢٥/٢١٦ * (+٦) + (١٩١/٢١٦) * (-١) = -٤١/٢١٦ = -١٨٫٩٨٢٪.
- المجموع 10 :
هناك ٢٧ طريقة لرمي ١٠ نردات: (١-٣-٦ * ٦ طرق، ١-٤-٥ * ٦ طرق، ٢-٢-٦ * ٣ طرق، ٢-٣-٥ * ٦ طرق، ٢-٤-٤ * ٣ طرق، ٣-٣-٤ * ٣ طرق). وبالتالي، تكون نسبة ربح اللاعب ٢٧/٢١٦ * (+٦) + (١٨٩/٢١٦) * (-١) = -٢٧/٢١٦ = -١٢٫٥٠٠٪.
- المجموع 11 : انظر المجموع 10
- المجموع 12 : انظر المجموع 9
- المجموع 13 : انظر المجموع 8
- المجموع 14 : انظر المجموع 7
- المجموع 15 : انظر المجموع 6
- المجموع 16 : انظر المجموع 5
- المجموع 17 : انظر المجموع 4
- رقمين :
لنفترض أن الرقمين المختارين هما ١ و٢. هناك ٣٠ تركيبة تتضمن ١ و٢: ١-٢-١ * ٣ طرق، ١-٢-٢ * ٣ طرق، ١-٢-٣ * ٦ طرق، ١-٢-٤ * ٦ طرق، ١-٢-٥ * ٦ طرق، ١-٢-٦ * ٦ طرق. وبالتالي، تكون نسبة ربح اللاعب ٣٠/٢١٦ * (+٥) + (١٨٦/٢١٦) * (-١) = -٣٦/٢١٦ = -١٦٫٦٦٧٪.
- ثلاثية محددة :
هناك طريقة واحدة فقط لرمي ثلاثية محددة. وبالتالي، تكون أفضلية اللاعب هي ١/٢١٦*(+١٨٠) + (٢١٥/٢١٦)*(-١) = -٣٥/٢١٦ = -١٦.٢٠٪.
- أي ثلاثية :
هناك ست طرق لرمي النرد الثلاثي. وبالتالي، تكون نسبة ربح اللاعب 6/216*(+30) +(210/216)*(-1) = -30/216 = -13.889%.
- زوج محدد :
لنفترض أن الزوج المختار هو واحد. هناك ١٦ طريقة لرمي نردين أو ثلاثة من هذا الرقم: ١+١+١، ١+١+٢ * ٣ طرق، ١+١+٣ * ٣ طرق، ١+١+٤ * ٣ طرق، ١+١+٥ * ٣ طرق، ١+١+٦ * ٣ طرق. وبالتالي، تكون نسبة ربح اللاعب ١٦/٢١٦ * (+١٠) + (٢٠٠/٢١٦) * (-١) = -٧٢/٢١٦ = -١٨.٥٢٪.
فيما يلي صيغة لعدد s من النقاط على عدد n من النرد، مأخوذة من كتاب نظرية المقامرة والمنطق الإحصائي لريتشارد أ. إبستاين، الصيغة 5-14.
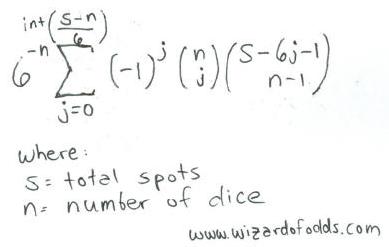
على سبيل المثال، دعنا نلقي نظرة على عدد الطرق للحصول على 11 نقطة على 3 نرد.
int[(sn)/6] = int[(11-3)/6] = int[1.33] = 1
المجموع سيكون 6 -3 * [-1 0 *combin(3,0)*combin(11-6*0-1,3-1) + -1 1 *combin(3,1)*combin(11-6*1-1,3-1) ] =
1/216 * [1*1*الجمع(10,2) + -1*3*الجمع(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12.5%
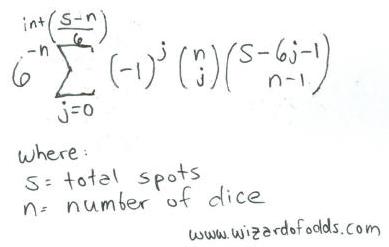










.png)










