WOO logo

يوصي المعالج

لغز المستطيل المطوي


في هذه النشرة الإخبارية أقدم لكم لغزًا رياضيًا من إصدار نوفمبر من نشرة مينسا.

لنفترض أن لديك مستطيلًا بمساحة ١×٤. الآن، اطوِ هذا المستطيل بحيث تتداخل زواياه المتقابلة، كما هو موضح في هذا الرسم التخطيطي.

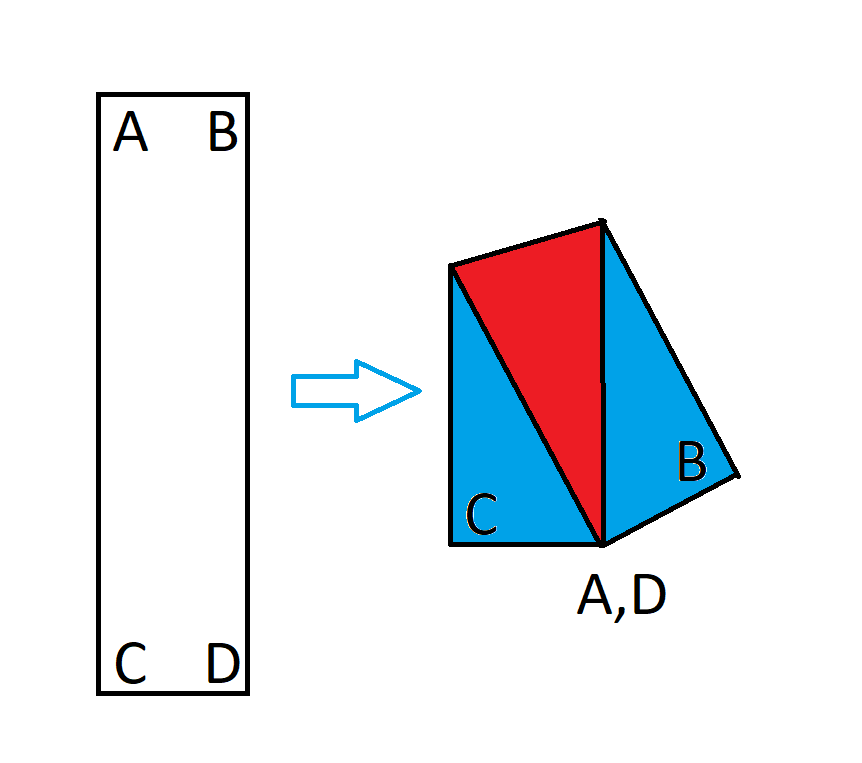
مستطيل 1 × 4

بعد طيّ المستطيل، يُشكّل شكلًا خماسيًا غير منتظم. ما نسبة الجزء الذي تتداخل فيه الورقة من هذا الشكل الخماسي إلى المساحة الكلية؟ بمعنى آخر، نسبة المساحة الحمراء في الصورة أعلاه إلى المساحة الكلية.

قم بالتمرير إلى الأسفل للحصول على الإجابة والحل.

إجابة

الإجابة هي 17/47 = تقريبًا 0.3617

حل

لتوضيح الحل، دعوني أُحدد بعض النقاط الإضافية، كما هو موضح في الصورة التالية. F هي نقطة المنتصف بين E وG.

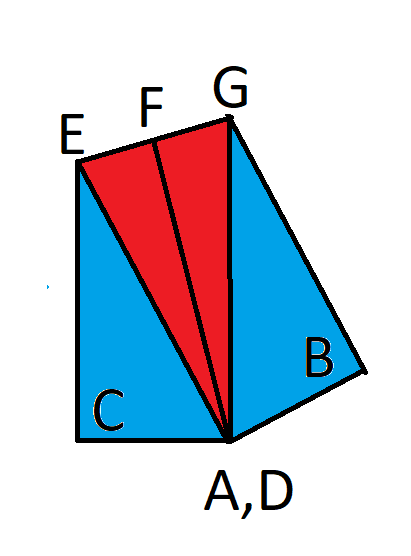
مستطيل 1x4، خماسي - الحل

نحن نعلم:

التيار المتردد = 1

CE + AE = 4

دعونا نحل AE باستخدام نظرية فيثاغورس:

1 2 + (CE) 2 = (AE) 2

عند استبدال 4 – CE بـ AE نحصل على:

1 2 + (CE) 2 = (4 – CE) 2

1 + (م) 2 = 16 – 8 (م) + (م) 2

8(CE) = 15

CE = 15/8

بالعودة إلى 1 2 + (CE) 2 = (AE) 2 ، يمكننا حل (AE) لأننا نعرف EC:

(AE) 2 = (CE) 2 + 1 2

(AE) 2 = (15/8) 2 + 1 2

(AE) 2 = 225/64 + 64/64

(AE) 2 = 289/64

6;font-family: 'Open Sans',sans-serif;color: #313131!important">AE = 17/8

قبل الطي، كان الطول من أ إلى د قطر المستطيل. باستخدام فيثاغورس مجددًا، يكون الطول هو الجذر التربيعي (17).

(AF) هو نصف هذا الطول، أو sqrt(17)/2.

بمعرفة AE وAF، يمكننا حل EF باستخدام فيثاغورس مرة أخرى:

(AE) 2 = (EF) 2 + (AF) 2

(17/8) 2 = (EF) 2 + (جذر(17)/2) 2

289/64 = (EF) 2 + 17/4

289/64 = (EF) 2 + 272/64

(EF) 2 = 17/64

EF = الجذر التربيعي(17)/8

كما ذكرنا سابقًا، F هي نقطة المنتصف بين E وG. هذا EG = 2*sqrt(17)/8 = sqrt(17)/4.

المثلث الأحمر، AEG = (1/2) × القاعدة × الارتفاع =

= (1/2) × جذر(17/4) × جذر(17)/2

= (1/2) × (17/8) = 17/16

مساحة المثلث ACE = (1/2)*القاعدة*الارتفاع =

(1/2) × 1 × (15/8) = 15/16.

مساحة الخماسي بالكامل = AEG + 2*ACE =

(17/16) + 2*(15/16) = 47/16

وبالتالي فإن مساحة المنطقة الحمراء إلى كامل الخماسي =

(17/16) / (47/16) = 17/47 = تقريبًا 0.3617


كتبه: Michael Shackleford