برهان قابلية القسمة على 3

هذا الأسبوع، سآخذ استراحة من تفاهات الرؤساء وأجرب شيئًا جديدًا. لطالما استمتعتُ بالبرهان الرياضي الجيد. إلى أن تنفد أفكاري، سأستعرض بعض النظريات الرياضية الشهيرة وأحاول شرح صحتها بأبسط طريقة ممكنة. بدايةً، سأُبيّن هذا الأسبوع أنه إذا كان مجموع أرقام أي عدد صحيح قابلًا للقسمة على 3، فإن العدد الصحيح قابل للقسمة على 3. ولكن، قبل ذلك، أقدم لكم لغز المنطق الأسبوعي المعتاد.

لغز المنطق

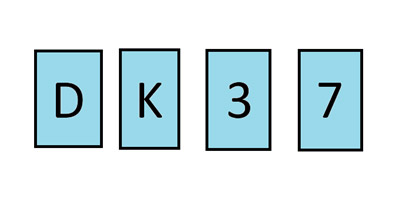
أربع بطاقات على طاولة. كما ترى، البطاقات المكشوفة مُعلّمة بـ D، K، 3، و7. تعلم أن كل بطاقة تحمل حرفًا على أحد وجهيها ورقمًا على الآخر. من المفترض أن هناك قاعدة تصنيع تنص على أن البطاقة التي تحمل حرف D على أحد وجهيها يجب أن تحمل الرقم 3 على الوجه الآخر. أي بطاقتين يجب قلبهما للتأكد من اتباع هذه القاعدة؟

الجواب سيكون في نهاية النشرة الإخبارية.

إثبات قابلية القسمة على 3

كما ذكر في المقدمة، يمكننا اختبار ما إذا كان العدد الصحيح قابلاً للقسمة بالتساوي على 3 على النحو التالي:

1. خذ مجموع الأرقام.
2. إذا كان المجموع وفقًا للقاعدة ١ قابلًا للقسمة على ٣ بالتساوي، فسيكون العدد الأصلي قابلًا للقسمة أيضًا. كذلك، إذا لم يكن المجموع قابلًا للقسمة على ٣، فلن يكون العدد الأصلي قابلًا للقسمة أيضًا.

لننظر إلى رقم هاتف البيت الأبيض، على سبيل المثال، وهو 2024567041. مجموع الأرقام هو 2+0+2+4+5+6+7+0+4+1 = 31. 31 لا يقبل القسمة على 3، وبالتالي فإن الرقم الأصلي لا يقبل القسمة أيضًا.

لإثبات نجاح هذا الأمر، قم بتقسيم الرقم الأصلي على النحو التالي:

6؛ عائلة الخطوط: 'Open Sans'، sans-serif؛ اللون: #313131 !important؛ ">2024567041 = (2*1000000000) + 0 + (2*10000000) + (4*1000000) + (5*100000) + (7*1000) + 0 + (4*10) + (1*1)

بعد ذلك، قم بتقسيم قوى العدد 10 إلى قسمين، 1 وباقي العدد:

= (2*(999999999+1)) + 0 + (2*(9999999+1)) + (4*(999999+1)) + (5*(99999+1)) + (7*(9999+1)) + 0 + (4*(9+1)) + (1*(0+1))

من الواضح أن أي عدد يحتوي على 9 جميعها قابل للقسمة بالتساوي على العددين 3. على سبيل المثال، 99999 = 3 * 33333.

وبناء على ذلك، دعونا نعيد ترتيب المصطلحات في الرقم أعلاه.

= (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) + (2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1)

من البديهي أن كل حد من الحدود السبعة الأولى قابل للقسمة على 3 بالتساوي، لأنها تقسم بالتساوي على عدد يحتوي على 9. بمعنى آخر، (2*999999999) + (2*9999999) + (4*99999) + (5*99999) + (7*9999) + (4*9) + (1*0) قابل للقسمة على 9 بالتساوي، لذا يُمكننا حذف هذا الجزء. لنترك لكم:

(2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1) = 2+0+2+4+5+6+7+0+4+1 = 31

هذا هو مجموع الأرقام، والذي يساوي 31. ونظرًا لأن هذا الجزء المتبقي لا يمكن قسمته بالتساوي على 3، فإن العدد بأكمله لا يمكن قسمته بالتساوي أيضًا.

تُستخدم هذه القاعدة نفسها لاختبار قابلية القسمة على 9. إذا كان مجموع أرقام العدد الأصلي قابلاً للقسمة على 9، فسيكون العدد بأكمله قابلاً للقسمة أيضًا. والعكس صحيح أيضًا، إذا لم يكن مجموع أرقام العدد قابلاً للقسمة على 9 بالتساوي، فلن يكون العدد بأكمله قابلاً للقسمة أيضًا.

حل لغز المنطق

دعونا نطلق على القاعدة التي تنص على أن 3 يجب أن يكون على الجانب الآخر من قاعدة D اسم قاعدة "D-3".

1. • من الواضح أنه يتعين علينا قلب بطاقة D للتأكد من أن الجانب الآخر هو 3.
2. • يجب أن يحتوي الجانب الآخر من بطاقة K على رقم.نظرًا لأن الجانب الآخر لا يمكن أن يحصل على D، فإن هذه البطاقة لا تساعدنا في دحض قاعدة D-3 التي تم اتباعها.
3. يجب أن يحتوي الوجه الآخر للبطاقة رقم 3 على حرف. إذا كان هذا الحرف D، فهو يدعم قاعدة D-3. أما وجود أي حرف آخر على الوجه الآخر، فلا يفيدنا. لذا، إما أن تكون هذه البطاقة متوافقة مع قاعدة D-3 أو لا تكون ذات صلة. في كلتا الحالتين، نبحث عن بطاقة تخالف القاعدة لإبطال قاعدة D-3. أي حرف موجود على الوجه الآخر لن يُبطل قاعدة D-3، لذا لا داعي للتحقق منه.
4. يجب أن يحتوي الوجه الآخر للبطاقة 7 على حرف. إذا كان هذا الحرف D، فإن هذه البطاقة تُبطل قاعدة D-3. لذا، يجب التحقق منها للتأكد من أنها ليست بطاقة D-7، وهو اختصار لادعاء D-3.

وبالتالي، فإن البطاقات D و7 هي البطاقات الوحيدة التي يجب التحقق منها.