WOO logo

يوصي المعالج

متطابقة أويلر

هذا الأسبوع نخوض تحديًا كبيرًا، وهو إثبات متطابقة أويلر. إن كنتم قد نسيتموها، فهي ربما أجمل متطابقة في الرياضيات: e ^(πi +1) = 0. أنا معجبٌ جدًا بهذه المتطابقة، حتى أنني كتبتها على بطاقة عملي، وربما أوشمها على جسدي. ولكن قبل ذلك، أقدم لكم لغز المنطق الأسبوعي المعتاد.

لغز منطقي

لديك أربع سلاسل تتكون كل منها من ثلاث حلقات. كيف يمكنك ربطها معًا لتكوين حلقة دائرية من جميع الحلقات الـ 12 مع قطع ثلاث حلقات فقط؟

إثبات متطابقة أويلر

تُعد معادلة أويلر واحدة من أشهر المعادلات في الرياضيات، والتي تنص على أن e πi +1 = 0. والمثير للدهشة فيها أنها تجمع بين أهم خمسة أرقام في الرياضيات: 0، 1، e، π و i.

يتطلب حلّي معرفة صيغة متسلسلة تايلور . وللتذكير، فهي كالتالي:

صيغة

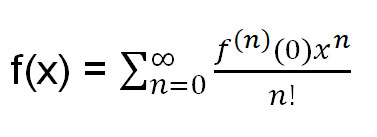
حيث f (n) (0) = المشتقة النونية لـ f(x) عند 0.

أجد هذه المعادلة شخصياً من أروع وأجمل المعادلات في الرياضيات. بالنسبة لي، هي دليل على وجود شيء إلهي في الرياضيات.

مع ذلك، إليك ثلاثة متسلسلات تايلور للدوال الشائعة التي سنحتاجها:

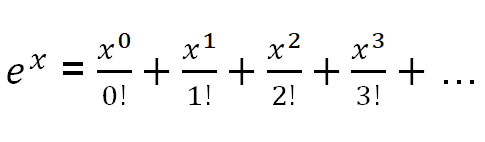
التوسعات
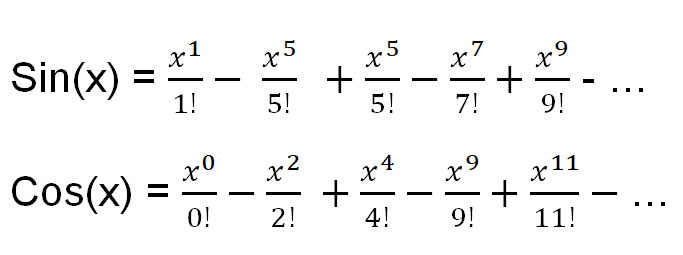
expansions

لنستخدم متسلسلة تايلور لـ e x لإيجاد e πi .

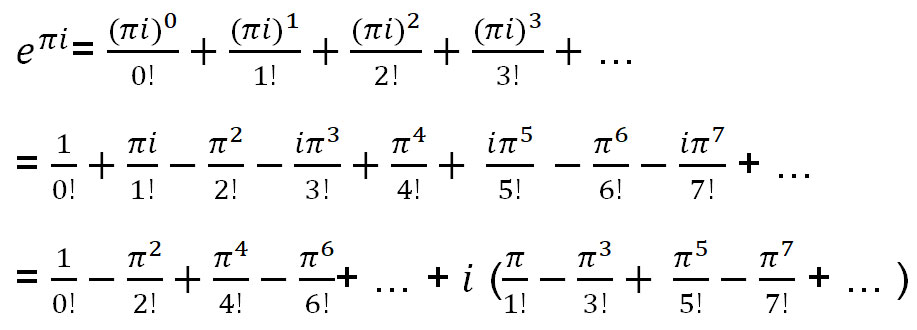
التوسعات

يمكن التعبير عن المعادلة أعلاه كدوال لـ sin(x) و cos(x):

= cos(π)+i × sin⁡(π)

= -1 + i × 0

= -1

إذن، لدينا e πi = -1. ويمكن إعادة ترتيب ذلك إلى الشكل المعتاد:

e πi +1 = 0

حل لغز المنطق

  1. خذ إحدى السلاسل الأربع وافتحها وافصل الحلقات الثلاث. سمِّ السلاسل الثلاث الأخرى 1 و2 و3.
  2. استخدم حلقة واحدة لدمج السلسلتين 1 و 2، مما يؤدي إلى إنشاء سلسلة مكونة من سبع حلقات.
  3. استخدم حلقة أخرى لدمج سلسلة الحلقات السبع من الخطوة 2 مع السلسلة 3، مما يؤدي إلى إنشاء سلسلة مكونة من 11 حلقة.
  4. استخدم الحلقة الأخيرة لربط طرفي السلسلة المكونة من 11 حلقة من الخطوة 3 لإنشاء دائرة مكونة من 12 حلقة.