كيفية تطبيق قواعد تصنيف الشطرنج

نتناول هذا الأسبوع طريقةً لتحسين تصنيفك في لعبة الشطرنج، دون تحسين أدائك إطلاقًا. مع العلم أن هذه ميزة صغيرة، وهي ذات أهمية أكاديمية بالأساس. ولكن، كالمعتاد، أقدم لكم لغز المنطق الأسبوعي.

لغز المنطق

هناك 50 شخصًا في صف واحد، مُرقَّمون من 1 إلى 50 تسلسليًا. الشخص الأول في الصف هو رقم 1. كل شخص إما أن يقول الحقيقة أو يكذب. الجميع يعلم صدق الآخرين.

كل الأشخاص ذوي الأرقام الزوجية يقولون: "كل من أمامي كاذب".

كل الناس ذوي الأرقام الفردية يقولون: "كل من خلفي كاذب".

من يقول الحقيقة؟

كيفية تطبيق قواعد تصنيف الشطرنج

نظام تصنيف الشطرنج الأكثر شيوعًا، على حد علمي، هو نظام إيلو. سُمي على اسم أرفاد إيلو. ويُستخدم النظام نفسه في ألعاب ورياضات أخرى.

تعتمد هذه الطريقة على صيغة تُحدد احتمال فوز أي لاعب في اللعبة بناءً على تقييميهما. يحصل الفائز على نقاط تتناسب مع احتمال خسارته، وكذلك الخاسر على نقاط تتناسب مع احتمال فوزه. تُمنح نقطة واحدة للفوز، و0.5 نقطة للتعادل، و0 نقطة للتعادل.

يعتمد النظام على الافتراض، الذي أتفق معه، والذي مفاده أن أداء اللاعب يمكن أن يتم تصميمه بعد رقم عشوائي مرسوم على منحنى الجرس، مع تصنيف اللاعب باعتباره المتوسط.اللاعب الذي يحصل على الرقم الأعلى يفوز.

الطريقة التي يتم بها تحديد احتمال الفوز هي كما يلي:

ليكن r1 = تصنيف اللاعب 1.

ليكن r2 = تصنيف اللاعب 2.

p = احتمال فوز اللاعب 1.

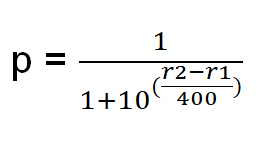
لنلقِ نظرة على مثال. لنفترض أن r1 = 1900 وr2 = 2000.

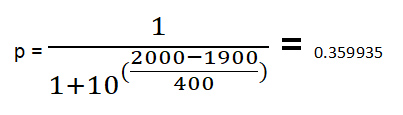
بافتراض أن 1 نقطة تُعطى للفوز و0 نقطة للخسارة، فإن الزيادة في التصنيف تكون 32* (النقاط الفعلية - احتمال الفوز).

في مثالنا السابق، إذا خسر اللاعب 1، كما هو متوقع، ينخفض تقييمه بمقدار 11.52 نقطة، ويرتفع تقييم اللاعب 2 بنفس المقدار. إذا فاز اللاعب 1، يرتفع تقييمه بمقدار 20.48 نقطة، وينخفض تقييم اللاعب 2 بنفس المقدار.

يعتمد نظام إيلو على انحراف معياري في الأداء، كما هو مُمَثَّل بطريقة الأرقام العشوائية الموضحة أعلاه، وهو 200. أفترض صحة هذا. مع ذلك، فإن صيغة احتمال الفوز، التي تُبنى عليها جداول إيلو، لا تتوافق مع هذا الانحراف المعياري، إلا إذا كان الفرق في التقييمات 0 أو 189.

الاحتمال الصحيح لفوز اللاعب الذي لديه تصنيف r1 هو:

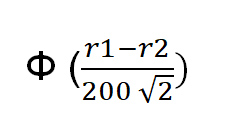
حيث الدالة Φ(x) = احتمال أن يكون المتغير العشوائي المعياري الطبيعي أقل من x. في إكسل، الصيغة الصحيحة هي norm.s.dist((r1-r2)/(200*sqrt(2)),1).

لننظر إلى حالة يكون فيها فرق التصنيف 100. لنفترض أن اللاعب 1 هو الأضعف. تشير صيغة ELO إلى أن احتمال فوز اللاعب 1 هو 35.99%. مع ذلك، فإن احتمال فوزه الفعلي، بناءً على انحراف معياري في الأداء قدره 200، هو 36.18%. بمعنى آخر، فوز اللاعب 1 باللعبة رهان جيد ورهان سيء للاعب 2. أُظهر أن الزيادة المتوقعة في تصنيف اللاعب 1 والخسارة المتوقعة للاعب 2 هي 0.06 نقطة.

لنلقِ نظرة الآن على فرق تصنيفات لعبة 300، حيث يكون اللاعب 1 هو الأضعف. هنا، تمنح صيغة Elo اللاعب 1 فرصة فوز بنسبة 15.10%، بينما أظهرتُ أنها 14.44%. هذا يجعل المشاركة في اللعبة رهانًا سيئًا للاعب 1 ورهانًا جيدًا للاعب 2. الخسارة المتوقعة للاعب 1 هي 0.21 نقطة، وكذلك الربح المتوقع للاعب 2.

إن الرياضيات التي تكمن وراء الاحتمالات الفعلية تعتمد على المنحنى الغاوسي وهي أكثر تعقيدًا مما أرغب في الخوض فيه في هذه النشرة الإخبارية.

خلاصة القول هي أنه إذا كان فارق النقاط أكثر من ١٨٩، فإن الفوز بالمباراة رهان جيد للفريق المرشح للفوز. وبالمثل، إذا كان أقل من ١٨٩، فإن الفوز بالمباراة رهان جيد للفريق الأضعف.

مع ذلك، التحيز ضئيل. لن أقبل أو أرفض الألعاب بناءً على هذه المعلومات. بل أعتقد أنه من الأفضل اختيار أي لعبة من أجل حب الشطرنج.

قراءة إضافية: مقالة ويكيبيديا عن نظام تصنيف ELO.

إجابة لغز المنطق

الشخصان 2 و 49 هما الوحيدان اللذان يقولان الحقيقة.

حل لغز المنطق

لنبدأ بالشخص الأول. إذا كان صادقًا، فالجميع يكذبون. أما الشخص الثالث، فيقول إن الجميع من سن الرابعة إلى الخمسين يكذبون.إذا كان ذلك صحيحًا، فالشخص الثالث صادق. أما الشخص الأول فيقول إنه يكذب. وهذا يؤدي إلى تناقض. وبالتالي، لا بد أن الشخص الأول يكذب.

الشخص الثاني يقول إن الشخص الأول يكذب فقط. هذا يجعل الشخص الثاني صادقًا.

كل شخص ذي رقم زوجي من ٤ إلى ٥٠ يقول إن الشخص الثاني يكذب. هذا يجعلهم جميعًا كاذبين.

الشخص ٤٩ يقول إن الشخص ٥٠ يكذب، وهذا صحيح. هذا يجعل الشخص ٤٩ صادقًا.

كل شخص رقمه فردي من ٣ إلى ٤٧ يقول إن الشخص ٤٩ يكذب. هذا يجعلهم جميعًا كاذبين.

وهكذا فإن الأشخاص الوحيدين الذين يقولون الحقيقة هم الرقمان 2 و49.