WOO logo

يوصي المعالج

برهان نظرية الزاوية المحيطية (الجزء 1)

نعود هذا الأسبوع إلى موضوعي المعتاد وهو إثبات نظرية رياضية. وهذه المرة، سنتناول نظرية الزاوية المحيطية. هذا البرهان أكثر تعقيدًا من المعتاد، لذا سأقسمه إلى جزأين، وسأنشر الجزء الثاني الأسبوع المقبل. ولكن قبل ذلك، أقدم لكم لغز المنطق الأسبوعي المعتاد.

لغز منطقي

في الرسم البياني أدناه، حرك عملة واحدة لتشكيل صفين من أربع عملات لكل صف.

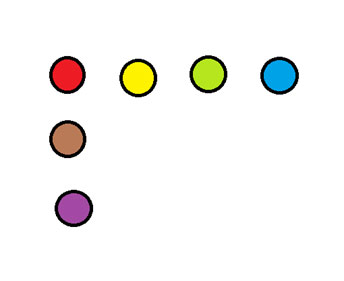
رسم بياني

يظهر الجواب في أسفل النشرة الإخبارية.

برهان نظرية الزاوية المحيطية (الجزء 1)

قبل شرح نظرية الزاوية المحيطية، دعوني أحدد بعض النقاط على الدائرة في الرسم التخطيطي التالي.

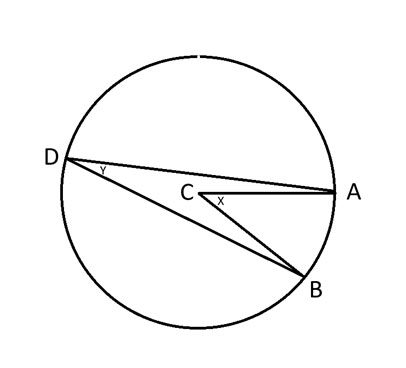
دائرة

أ، ب، د = أي ثلاث نقاط على الدائرة.

ج = مركز الدائرة.

x = الزاوية ACB.

ص = الزاوية أ ب ب.

تنص نظرية الزاوية المحيطية على أن الزاوية 2y = x.

في هذه النشرة، سأسعى لإثبات ذلك في الحالة الخاصة التي يشكل فيها AD أو BD قطرًا للدائرة. في الأسبوع المقبل، سأتوسع في ذلك للحالة العامة لموقع D.

لنسمي الحالة المحددة التي يشكل فيها AD قطرًا للدائرة الحالة 1. إليك رسم تخطيطي جديد لتلك الحالة.

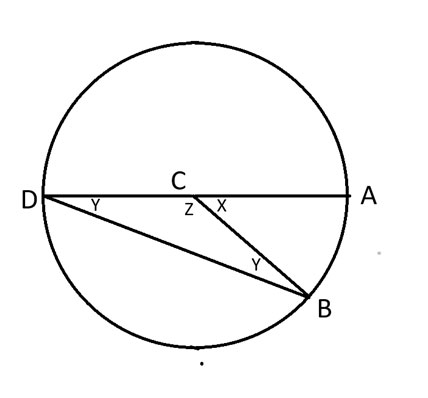
إعلان تخطيطي

في الرسم التخطيطي أعلاه، يشكل AD قطراً للدائرة التي تقع C في مركزها.

يمكننا القول أن x+z = 180 درجة، لأنها تشكل نصف مجموع 360 درجة للدائرة.

يشكل المثلث BCD مثلثًا متساوي الساقين. وبالتالي، فإن الزاوية CDB = CBD = y.

كما هو موضح في رسالتي الإخبارية بتاريخ 13 نوفمبر 2025، فإن مجموع الزوايا الداخلية للمثلث يساوي 180 درجة. بعبارة أخرى، z + 2y = 180 درجة.

لنعد كتابة المعادلتين:

z = 180 – x

z = 180 – 2y

لنضع كليهما في معادلة، لأنهما كلاهما يساوي z.

180 – س = 180 – 2ص

-س = -2ص

x = 2y.

لقد أثبتنا بذلك الحالة الخاصة لنظرية الزاوية المحيطية، حيث تشكل نقطتان على الدائرة قطراً. سنبني على هذا في الأسبوع القادم لإثباتها في الحالة العامة.

حل لغز المنطق

انقل العملة الزرقاء فوق العملة الحمراء. في الرسم البياني أدناه، تُظهر الأرقام عدد العملات في كل كومة.

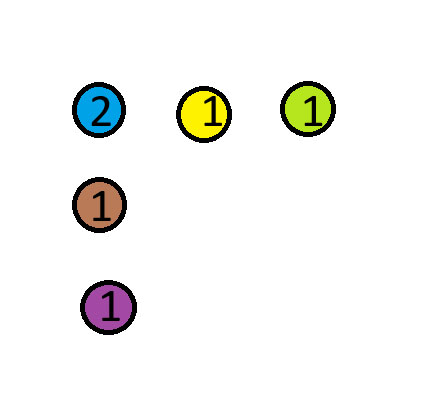
عملات معدنية

شكر وتقدير: حصلت على هذا اللغز من قناة Mind Your Decisions على يوتيوب. هذا هو اللغز رقم 3 في الفيديو المرفق.