برهان نظرية الزاوية المحيطية (الجزء الثاني)

ربما تتذكرون أنني بدأت الأسبوع الماضي بإثبات نظرية الزاوية المحيطية. هذا الأسبوع، سننهيها. ولكن قبل ذلك، أقدم لكم لغز المنطق الأسبوعي المعتاد.

لغز منطقي

أي من العبارات التالية صحيحة؟

1. إحدى هذه العبارات خاطئة.
2. اثنان من هذه العبارات خاطئان.
3. ثلاثة من هذه العبارات خاطئة.
4. أربع من هذه العبارات خاطئة.
5. خمس من هذه العبارات خاطئة.
6. ستة من هذه العبارات خاطئة.
7. سبعة من هذه العبارات خاطئة.
8. ثمانية من هذه التصريحات خاطئة.
9. تسع من هذه العبارات خاطئة.
10. عشر من هذه العبارات خاطئة.

يظهر الجواب في أسفل النشرة الإخبارية.

نظرية الزاوية المحيطية (الجزء 2)

دعني أذكرك بما تنص عليه نظرية الزاوية المحيطية.

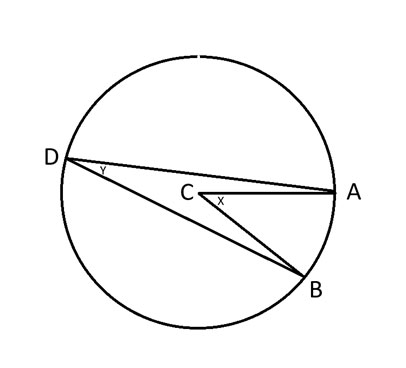
أ، ب، د = أي ثلاث نقاط على الدائرة.

ج = مركز الدائرة.

x = الزاوية ACB.

ص = الزاوية أ ب ب.

تنص نظرية الزاوية المحيطية على أن الزاوية 2y = x.

في الأسبوع الماضي، أثبتُ صحة هذا في الحالة الخاصة التي يكون فيها AD أو BD قطرًا للدائرة. سأستخدم ذلك هذا الأسبوع لإثبات صحة النظرية في الحالة العامة لـ D.

سأقوم بتحليل جميع المواقع المحتملة لـ D على النحو التالي:

الحالة 1 = AD أو BD يشكلان قطرًا للدائرة (تم إثبات ذلك الأسبوع الماضي)

الحالة 2 = تقع النقطة D (أو هل هي "تقع"؟) على طول القوس على الجانب المقابل من الدائرة من النقطتين A و B.

الحالة 3 = جميع الحالات الأخرى

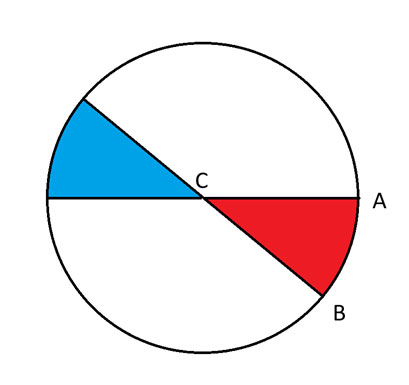
بمعنى آخر، ستغطي الحالة الثانية الحالات التي يكون فيها D على طول حافة الدائرة في المنطقة الزرقاء. أما الحالة الثالثة فستغطي المواقع الأخرى خارج تلك الشريحة الزرقاء.

لنستخدم الرسم التخطيطي التالي للمناقشة.

يترك:

س = س1 + س2

ص = ص1 + ص2

z = z1 + z2

نسعى لإثبات أن x = 2y

رسمتُ خطاً دقيقاً من النقطة د إلى النقطة ج، مشكلاً قطراً للدائرة. النقطة هـ هي نقطة تقاطع هذا الخط مع الجانب الآخر من الدائرة.

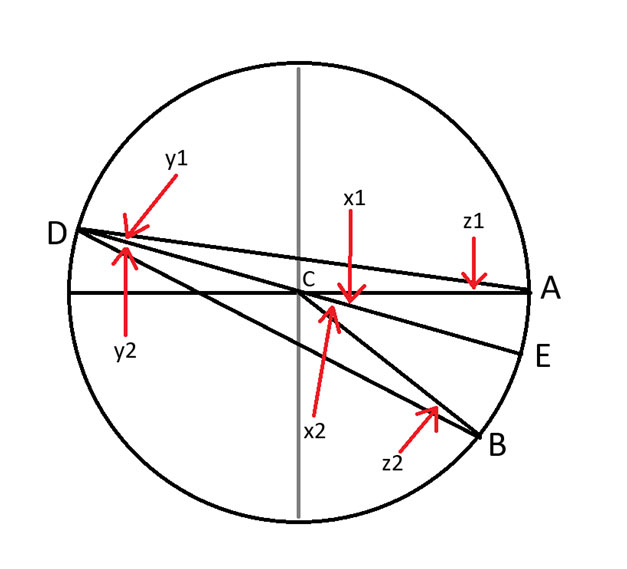
كان ينبغي أن تكون الأرقام في الزوايا مكتوبة بخط سفلي، لكن برنامج الرسم الخاص بي لم يسمح بذلك.

لننظر إلى المثلث ADE.

بما أن DE يشكل قطرًا، يمكننا استخدام ما أثبتناه الأسبوع الماضي لإظهار 2x1 = 2y1.

والآن لننظر إلى المثلث EDB.

وبنفس المنطق، 2x ₂ = y ₂ .

بإضافة هذه المعادلات:

2x ₁ + 2x ₂ = y ₁ + y ₂

2( _x1 + _x2 ) = _y1 + _y2

2x = y

وهكذا انتهينا من الحالة الثانية.

لنلقِ نظرة على الحالة الثالثة.

نسعى هنا إلى إثبات أن 2x ₁ = y ₁ .

من الحالة 1:

_2x² = _y²

2(x ₁ + x ₂ ) = y< ₁ +y ₂

بطرح المعادلة العليا من المعادلة السفلى:

2x ₁ = y ₁

وقد أثبتنا الحالة الثالثة.

حل لغز المنطق

العبارة التاسعة فقط هي الصحيحة.

حل لغز المنطق

لدينا عشرة تصريحات متناقضة. إذا كان لديك عشرة أشخاص يقولون أشياء مختلفة، فإما أن يكون شخص واحد منهم على صواب أو لا أحد منهم على صواب.

لنفترض أن جميع العبارات العشر خاطئة. في هذه الحالة، ستكون العبارة رقم 10 صحيحة. وهذا يعني أن تسع عبارات فقط ستكون خاطئة. وبالتالي، يوجد تناقض. لا بد من وجود عبارة صحيحة. ولكن ما هي؟

إذا كانت عبارة واحدة صحيحة، فإن تسع عبارات خاطئة. العبارة رقم 9 هي التي تقول ذلك. وبالتالي، فإن العبارة رقم 9 فقط هي الصحيحة.