لغز رياضيات كبير لمكالمة زووم
طُرح السؤال التالي في نشرتي الإخبارية الأسبوع الماضي. للتذكير، إليك السؤال.
سؤال
لنفترض أن جميع أعضاء مجلس النواب الأمريكي، البالغ عددهم 435 عضوًا، انضموا إلى مكالمة زووم واحدة، من التاسعة صباحًا إلى العاشرة صباحًا. مع ذلك، ليس من الضروري حضور المكالمة كاملةً، بل جزء منها فقط. يختار كل عضو عشوائيًا لحظةً محددةً للدخول والخروج، ضمن نطاق الساعة الواحدة.
ما احتمال أن يتداخل حضور ممثل واحد على الأقل مع حضور جميع الممثلين الآخرين في المكالمة؟ بمعنى آخر، رؤية وجوه جميع الأعضاء الآخرين خلال فترة حضوره، وليس بالضرورة جميعهم في نفس الوقت.
يرجى التمرير عبر هذه الصور لرؤية إجابتي والحلي.


إجابة
2/3
حل
استراتيجيتي العامة في الأسئلة التي تشمل مجموعة كبيرة من الأشخاص هي البدء بشخصين. بعد إيجاد الإجابة، أنتقل إلى ثلاثة. ثم، إذا لم يكن الأمر صعبًا جدًا، أنتقل إلى أربعة. إذا لاحظتُ نمطًا معينًا، فمن المرجح أن ينطبق هذا النمط على أي عدد من الأشخاص.
مراجعة الرياضيات الأساسية
قبل الخوض في التفاصيل، سأستخدم دالة combin(x,y) بشكل متكرر. هذا هو عدد طرق اختيار y عنصر من مجموعة x. على سبيل المثال، عدد طرق اختيار خمس بطاقات من أصل 52، حيث لا يهم الترتيب، هو combin(52,5) = 2,598,960. يمكن التعبير عن الإجابة بالصيغة x! / (y! * (xy)!).
في هذه الحالة، لا تعني علامة التعجب أنني أصرخ، بل تُمثل دالة العامل. هذا هو عدد طرق ترتيب أي عدد مُحدد من العناصر. على سبيل المثال، إذا كنتَ بحاجة لقراءة ستة كتب، كتابًا واحدًا في كل مرة، فإن عدد الطلبات الممكنة للكتب هو 6!. إجابة الحالة العامة لـ n هي 1*2*3*…*n. في حالة الكتب الستة، الإجابة هي 1*2*3*4*5*6 = 720.
قضية شخصين
بعد ذلك، لنحل مسألة حالة الشخصين. لا يهم التوقيت الدقيق لدخول وخروج الأشخاص من المكالمة، المهم هو ترتيب الأحداث. لنستخدم حرفًا لتمثيل دخول/خروج شخص معين من المكالمة. بدءًا من اليسار، يمثل الاستخدام الأول للحرف دخول المكالمة، والثاني مغادرتها.
6;font-family: 'Open Sans',sans-serif;color: #313131!important">من بين الأماكن الأربعة في سجل المكالمات، هناك combin(4,2)=6 طرق يمكنك من خلالها وضع الحرف A:1. AABB
2. أباب
3. أبا
4. باب
5. بابا
6. بي بي ايه ايه
دعنا نتحقق مما إذا كان كلا المتصلين متصلين في نفس الوقت في كل سيناريو:
1. AABB - لا، جاء A وغادر قبل أن ينضم B إلى المكالمة.
2. ABAB - نعم، كان هناك تداخل بين وصول B ومغادرة A.
3. آبا - نعم، كان هناك تداخل بين وصول ب ومغادرته.
4. BAAB - نعم، كان هناك تداخل بين وصول A ومغادرة A.
5. بابا - نعم، كان هناك تداخل بين وصول أ ومغادرة ب.
6. BBAA - لا، جاء B وغادر قبل أن ينضم A إلى المكالمة.
كل سيناريو محتمل بنفس القدر. أربعة من أصل ستة سيناريوهات تداخلت، وبالتالي فإن احتمال التداخل في حالة الشخصين هو ٢/٣.
قضية ثلاثة أشخاص
عدد سجلات المكالمات في حالة الأشخاص الثلاثة هو حاصل ضرب عدد الطرق التي يمكن للشخص (أ) من خلالها اختيار مكانين من أصل 6 أماكن في السجل، وعدد الطرق التي يمكن للشخص (ب) من خلالها اختيار مكانين من أصل 4 أماكن متبقية. هذا يساوي combin(6,2)*combin(4,2) = 15*6 = 90.
سيكون من الممل سرد جميع التسعين. لنبسط الأمور بافتراض انضمام الشخص أ أولاً. لا بد أن يكون أحدهم أولًا، لذا قد يكون أ.
أولاً، لنفترض أن الحدث التالي في سجل المكالمات هو مغادرة أ. لنمثل هذا بـ AA????. بغض النظر عن كيفية دخول ب و ج إلى المكالمة ومغادرتهما لها، لن يتداخل أي منهما مع أ. وبالتالي، فإن احتمال نجاح سيناريو AA هو 0. واحتمال سيناريو AA نفسه هو 1/5، لأنه بعد أن احتل أ المركز الأول، كان هناك خمسة أحداث محتملة للوقوع بعد ذلك: أ، ب، ب، ج، ج.
ثانيًا، لننظر في الحالة التي ينضم فيها A أولاً، ثم يدخل B، ثم يغادر A. في هذه الحالة، يمثل B أي شخص آخر غير A (الذي أنهى المكالمة بالفعل). يُمثَّل هذا بـ ABA???. الأحرف المتبقية التي يجب وضعها هي B وC وC. من بين الطرق الثلاث التي يمكن بها وضع B (BCC وCBC وCCB)، ينتج عن CBC وCCB تداخل B مع كلٍّ من A وC.وبالتالي، فإن احتمال النجاح في سيناريو ABA هو ٢/٣. واحتمال هذا السيناريو نفسه هو pr(انضمام أي شخص غير A)*pr(خروج A) = (٤/٥)*(١/٤) = ١/٥، حيث pr(x) يمثل احتمال الحدث x.
ثالثًا، لننظر إلى الحالة التي ينضم فيها A أولًا، ثم يدخل B، ثم يغادر B. يُمثَّل هذا بـ ABB???. الأحرف المتبقية التي يجب وضعها هي A وC وC. من بين الطرق الثلاث التي يمكن بها وضع A (ACC وCAC وCCA)، ينتج عن CAC وCCA تداخل A مع كلٍّ من B وC. وبالتالي، فإن احتمال النجاح في سيناريو ABB هو 2/3. واحتمال هذا السيناريو نفسه هو pr (انضمام أي شخص آخر غير A) * pr (خروج B) = (4/5) * (1/4) = 1/5.
رابعًا، لننظر إلى الحالة التي ينضم فيها A أولاً، ثم يدخل B، ثم ينضم C. يُمثَّل هذا بـ ABC???. الأحرف المتبقية التي يجب وضعها هي A وB وC. من السهل ملاحظة أنه أينما يغادر A المكالمة، سيتداخل مع B وC. لذا، فإن احتمال النجاح في هذا السيناريو هو 1. احتمال هذا السيناريو نفسه هو pr (انضمام أي شخص آخر غير A) * pr (انضمام الشخص الثالث) = (4/5) * (2/4) = 2/5.
لقد تناولنا كل سيناريو محتمل، كما يتضح من الاحتمالات (1/5 + 1/5 + 1/5 + 2/5) مجموعها 1. وبأخذ حاصل الضرب النقطي لاحتمال كل سيناريو واحتمال نجاحه نحصل على: (1/5)*0 + (1/5)*(2/3) + (1/5)*(2/3) + (2/5)*1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3.
قضية أربعة أشخاص
لو كان وقتي ضيقًا، لظننتُ أن إجابة السؤال الأصلي هي ٢/٣، لأنها تنطبق على حالتي الشخصين والثلاثة. مع ذلك، يبدو هذا غير مُرضٍ، لذا لننتقل إلى حالة الأربعة أشخاص.أستطيع تقسيم الأمر إلى عشرة سيناريوهات محتملة، على النحو التالي:
- آآآ؟؟؟؟
احتمال السيناريو = 1/7
احتمال النجاح = 0 (لا يمكن لأحد أن يتداخل مع أ)
- أبا ؟؟؟؟
احتمال السيناريو = 1/7
احتمال النجاح = 16/30
- أبا ؟؟؟؟
احتمال السيناريو = 1/35
احتمال النجاح = 0 (لا يمكن لأحد أن يتداخل مع ب)
- ايه بي سي ؟؟؟؟
احتمال السيناريو = 4/35
احتمال النجاح = 2/3
- ايه بي سي ايه ؟؟؟؟
احتمال السيناريو = 4/35
احتمال النجاح = 5/6
- ايه بي سي بي ايه ؟؟؟؟
احتمال السيناريو = 1/35
احتمال النجاح = 2/3
- ايه بي سي بي سي ؟؟؟؟
احتمال السيناريو = 1/35
احتمال النجاح = 2/3
- أ ب ب د ؟؟؟؟
احتمال السيناريو = 2/35
احتمال النجاح = 1 (أ سوف يتداخل مع ب، ج، د)
- ايه بي سي سي ؟؟؟؟
احتمال السيناريو = 4/35
احتمال النجاح = 5/6
- أ ب ج د ؟؟؟؟
احتمال السيناريو = 8/35
احتمال النجاح = 1 (أ سوف يتداخل مع ب، ج، د)
أعتذر عن عدم تناول الرياضيات لكل موقف بعناية، لكنني لم أرغب في أن يستغرق هذا الحل وقتًا طويلاً وأردت ترك بعض العمل للقارئ.
يوضح الجدول التالي جميع السيناريوهات العشرة للقضية المكونة من أربعة أشخاص.
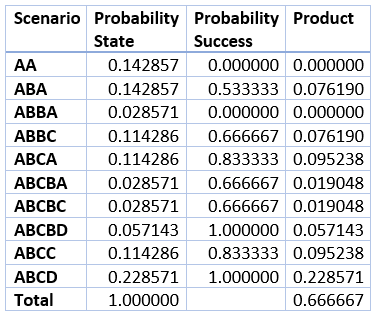
تُظهر الخلية الموجودة في أسفل يمين الجدول احتمالية 2/3.
ملخص
لقد أظهرنا احتمالًا قدره ٢/٣ للحالات المكونة من شخصين، وثلاثة، وأربعة أشخاص. ومن المنطقي أن يستمر هذا الاحتمال لأي عدد من الأشخاص. وقد أثبتت عمليات المحاكاة والحسابات التي أجراها أشخاص أذكى مني صحة هذا.

