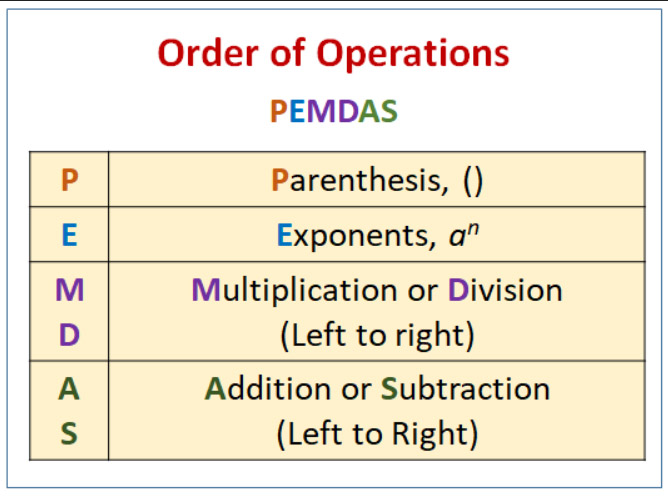
كيفية تطبيق قاعدة PEMDAS.

إذا كنت مثلي، فستجد في بثك المباشر على فيسبوك عددًا لا حصر له من أسئلة ترتيب العمليات. وتتبعها مئات الإجابات في التعليقات، أغلبها خاطئ. أما عدد من يعترفون بخطئهم فهو صفر دائمًا.

ما الذي يجعل رأيي صحيحًا؟ أولًا، إذا سمحتم لي بالحديث عن نفسي، أود أن أعتبر نفسي مرجعًا رائدًا في رياضيات ألعاب الكازينو. ابحثوا عن أي لعبة كازينو أو مصطلح، وستجدون اسمي في كل مكان. إضافةً إلى ذلك، لديّ شهادة في الرياضيات والاقتصاد من جامعة كاليفورنيا في سانتا باربرا، وأنا عضو متقاعد في جمعية الاكتواريين. مهما كان ما أفعله منذ تخرجي من الجامعة، فهو ذو طابع رياضي.

ومن الأمثلة على هذا السؤال:

6 ÷ 2 (1 + 2) = ؟

توقف لحظة وحاول معرفة ذلك.

إذا كانت إجابتك ١، فأنت مخطئ. أظن أنك مخطئ لأنك تتبع قاعدة PEMDAS العامة لترتيب العمليات. هذه قاعدة تُدرّس في الصف الخامس تقريبًا. إحدى طرق تذكرها التي تعلمتها هي "من فضلك، معذرة عمتي العزيزة سالي". الغرض منها تعليم الأطفال تقييم التعبيرات بالترتيب التالي:

1. 1. قوسين
2. 2. الأسس
3. 3. الضرب
4. 4. القسمة
5. 5. الحساب
6. 6. الطرح

ربما كان معلمك في المدرسة الابتدائية يعتقد حقًا أن هذا صحيح. ومع ذلك، فهو ليس كذلك. لا أعرف من أين بدأ، لكنني أظن أنه أسلوب مبسط للذاكرة يفهمه الأطفال في سن العاشرة بسهولة. تكمن مشكلة تبسيط أي شيء في أنه، وإن كان قد يؤدي إلى الإجابة الصحيحة في أغلب الأحيان، إلا أن هناك استثناءات للقاعدة.في حالة PEMDAS، فسيؤدي ذلك إلى قيام شخص ما بحل مشكلة 6 ÷ 2 (1 + 2) المذكورة سابقًا بهذه الطريقة:

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) لأنك تقوم بتقييم الأقواس أولاً
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 لأنه لا يوجد عامل خارج الأقواس يعني الضرب
3. 6 ÷ 2 × 3 = 6 ÷ 6 لأن الضرب يتم قبل القسمة، وفقًا لـ PEMDAS
4. 6 ÷ 6 = 1

يكمن الخطأ في المنطق أعلاه في الخطوة الثالثة. الضرب لا يأتي دائمًا قبل القسمة. هما متساويان في الأولوية. عندما يظهر كلاهما في نفس التعبير، ابدأ بالآخر على اليسار.

أود أن أضيف أنه ليس بالضرورة أن يسبق الجمع الطرح. فهما متساويان في الأولوية. ومع ذلك، في حالة الجمع والطرح، حيث لا تنطبق قواعد أعلى، لا يهم أيهما تبدأ.

هذه هي الطريقة الصحيحة لتقييم 6 ÷ 2 (1 + 2):

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) لأنك تقوم بتقييم الأقواس أولاً
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 لأنه لا يوجد عامل خارج الأقواس يعني الضرب
3. 6 ÷ 2 × 3 = 3 × 3 لأنه في كل من الضرب والقسمة، يتم التقييم من اليسار أولاً
4. 3 × 3 = 9

وهنا سؤال آخر لك:

7 + 7 ÷ 7 + 7 × 7 – 7 = ؟

على فيسبوك، تجد الإجابة ٥٦. هذا خطأٌ يرتكبه الناس، ليس بسبب PEMDAS، بل لأن "آلتي الحاسبة قالت إن الإجابة ٥٦". هذه إجابةٌ خاطئةٌ وغير دقيقة، يُقدمها من يكتفون بالتنقل من اليسار إلى اليمين.السبب الخاطئ هو:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 14 ÷ 7 + 7 × 7 – 7 لأنك تقيم من اليسار أولاً
2. 14 ÷ 7 + 7 × 7 – 7 = 2 + 7 × 7 – 7 لأنك تقيم من اليسار أولاً
3. 2 + 7 × 7 – 7 = 9 × 7 – 7 لأنك تقيم من اليسار أولاً
4. 9 × 7 – 7 = 63 – 7 لأنك تقيم من اليسار أولاً
5. 63 – 7 = 56

الطريقة الصحيحة لتقييم هذا الأمر هي:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 7 + 1 + 7 × 7 – 7 لأن القسمة تحل محل الجمع وتقع على يسار الضرب
2. 7 + 1 + 7 × 7 – 7 = 7 + 1 + 49 – 7 لأن الضرب يتفوق على الجمع والطرح
3. 7 + 1 + 49 – 7 = 8 + 49 – 7 لأنه بين الجمع والطرح يتم إجراء العملية التي تقع في أقصى اليسار أولاً
4. 8 + 49 – 7 = 57 – 7 لأنه بين الجمع والطرح نقوم بالعملية التي على أقصى اليسار أولاً
5. 57 – 7 = 50

لاحظ أن هذا أمرٌ صحيحٌ في نظام PEMDAS. يخطئ الناس في استخدامه لعدم استخدامه الآلات الحاسبة بشكل صحيح. من الضروري ترتيب الأرقام والعمليات الحسابية بالترتيب الصحيح. هذا أسهل بكثير مع الآلات الحاسبة التي تستخدم التدوين البولندي العكسي، مثل HP15C. بالمناسبة، أي شخص يمتلك HP15C أو 12C هو صديقي على الفور.

ختامًا، أودُّ أن أُضيفَ لمسةً خاصةً إلى ألغاز ترتيب العمليات هذه، من حيث منطقها وتصميمها. أعترفُ أنني سرقتُ الصور من جوجل. استُلهم هذا اللغز من لغزٍ مشابه، ولكنه أصعب، من قناة "انتبه لقراراتك" على يوتيوب. أرجو أن تنشروه بأنفسكم أينما شئتم؛ آملُ أن ينتشر على نطاقٍ واسع.

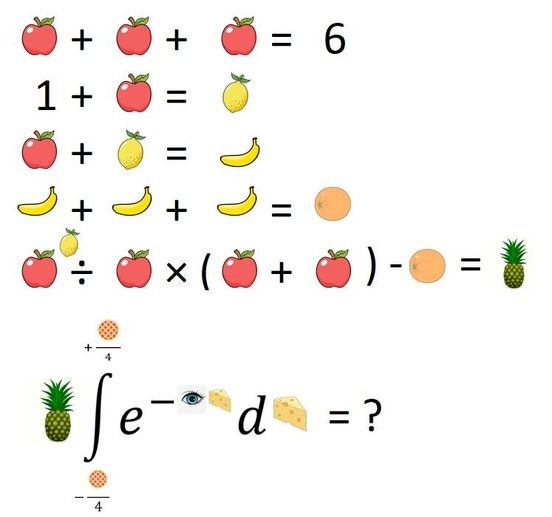
يتم منح جزء من الائتمان لحل الأناناس فقط والائتمان الكامل لحل التكامل.

سأنشر الإجابات في نشرة ٢٩ يونيو. إلى ذلك الحين، أتمنى أن تكون حظوظكم دائمًا في صالحكم.

كتبه: Michael Shackleford