جنون مارس 2025

لغز المنطق

قبل أن نصل إلى موضوع إحصائيات بطولة مارس لهذا الأسبوع، حان وقت لغزنا المنطقي الأسبوعي المعتاد. ها هو.

يلعب ثلاثة لاعبين لعبة. تُقذف ثلاث عملات معدنية، واحدة لكل لاعب، دون أن يراهم أحد. بناءً على نتيجة رمي كل عملة، يُعصب عينا اللاعب، ثم تُعطى له قبعة سوداء أو بيضاء. تُزال العصابة، ويُسمح لكل لاعب برؤية قبعات اللاعبين الآخرين، ولكن ليس قبعته.

يُمنح كل لاعب ورقة اقتراع سرية لتسجيل لون قبعته. الخيارات هي الأسود، والأبيض، والموافق. لنجاح التجربة، يجب أن تكون جميع أصوات اللاعبين الثلاثة صحيحة. أما إذا صوّت جميع اللاعبين الثلاثة "موافق"، فإن التجربة تُعتبر فاشلة.

يُمنح اللاعبون بعض الوقت لوضع استراتيجياتهم. ما هي الاستراتيجية التي يمكنهم استخدامها لتحقيق نسبة نجاح ٧٥٪؟

تحديثات بطولة مارس مادنس

كنتُ أراهن بكثافة على رهانات بطولة مارس مادنس. ومن الأمثلة الشائعة على ذلك رهانات "أكثر/أقل" على إجمالي عدد المباريات التي ستفوز بها فرق في مؤتمر المحيط الهادئ 12. ولتقييم هذه الرهانات، كان من المفيد معرفة عدد المباريات التي يتوقع فوز أي فريق مصنف.

تُحسم بعض الرهانات في الجولة الأولى. على وجه الخصوص، هل سيفوز فريق مصنف بـ ١٣ تصنيفًا أو أكثر بالمباراة؟ إليك بعض الأمثلة من رهانات هذا العام.

هذا العام، كان صاحب أدنى تصنيف (أو أعلى رقم تصنيف) للفوز هو 12. لذا، لم يكن أي من الرهانات المذكورة أعلاه ليفوز.

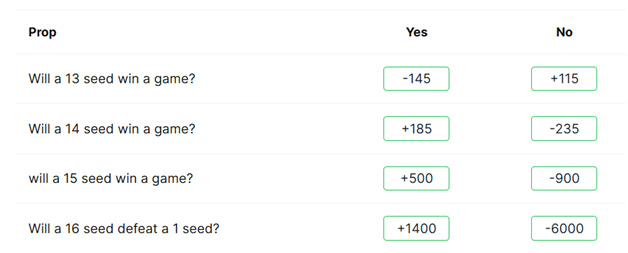
يوضح الجدول التالي احتمالية فوز أي فريق مصنف بمباراة في الجولة الأولى، بالإضافة إلى احتمالية فوز أي من الفرق الأربعة المصنفة. ويستند الجدول إلى أربعين عامًا من بطولة الرابطة الوطنية لرياضة الجامعات (NCAA) من عام ١٩٨٥ إلى عام ٢٠٢٥.

بذرة	انتصارات فريق محددة	أي فريق يفوز بالجولة الأولى
1	98.75%	100.00%
2	92.50%	100.00%
3	85.63%	99.96%
4	79.38%	99.82%
5	64.38%	98.39%
6	61.25%	97.75%
7	61.25%	97.75%
8	50.00%	93.75%
9	50.00%	93.75%
10	38.75%	85.93%
11	38.75%	85.93%
12	35.63%	82.83%
13	20.63%	60.31%
14	14.38%	46.25%
15	7.50%	26.79%
16	1.25%	4.91%

هذا العام، كان متوسط تصنيف المصنفين الذين نجحوا في تجاوز الدور الأول ٥.٣٤. أما المتوسط العام للبطولة فهو ٥.٨٤.

في الجولة الثانية، كان متوسط تصنيفات الفرق المؤهلة للتأهل إلى دور الستة عشر 3.44. أما متوسط تصنيفات البطولة فهو 4.52. أما أقل تصنيفات الفرق المؤهلة للتأهل بعد مباراتين فكان 10. بمعنى آخر، لم يُقدم الفريق الأضعف أداءً جيدًا هذا العام في الجولتين الأوليين.

في الجولة الثالثة، كان متوسط تصنيفات البقاء في دور الثمانية 1.625. أما متوسط البطولة فهو 3.30. أما أقل تصنيف تأهل لثلاث مباريات فكان 3 مباريات، منها مباراة واحدة فقط. هذا يعادل الرقم القياسي للبطولة لأدنى تصنيف تأهل، وهو 3 مباريات. وقد حدث هذا مرتين سابقًا، في عامي 2007 و2009. ويُسجل متوسط تصنيف البقاء 1.625، وهو رقم قياسي منخفض جديد في تاريخ البطولة.

في الدور نصف النهائي، حصدت جميع الفرق الأربعة المركز الأول. حدث هذا مرة واحدة فقط في تاريخ البطولة، عام ٢٠٠٨. هناك رهان شائع على العدد الدقيق للفرق المصنفة من الدرجة الأولى التي ستتأهل إلى الدور نصف النهائي. إليكم هذا الرهان من Covers هذا العام.

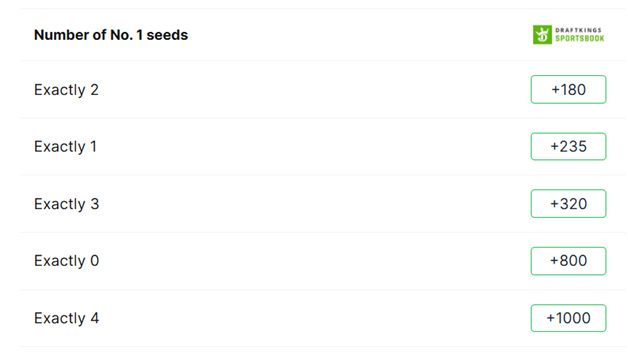
يوضح الجدول التالي عدد المصنفين الأول الذين وصلوا إلى الدور نصف النهائي خلال 40 عامًا من تاريخ البطولة.

#1 البذور	عدد	احتمال
4	2	5.00%
3	4	10.00%
2	15	37.50%
1	16	40.00%
0	3	7.50%
المجموع	40	100.00%

احتمال وصول أي مصنف رقم واحد إلى الدور قبل النهائي هو 41.25%.

لا شك أن وجود الفرق الأربعة المتأهلة إلى الدور قبل النهائي كفرق مصنفة رقم واحد يعني أن فريقين مصنفين رقم واحد سيتأهلان إلى المباراة النهائية وسيفوزان بها أيضًا.

رهان آخر هو احتمالية فوز الفريق الفائز بمباراة البطولة. إليكم رهانات "كوفر" لهذا العام.

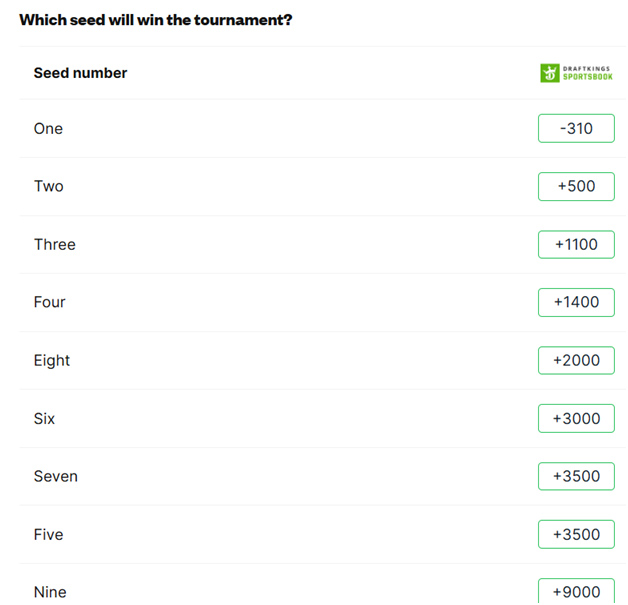
يوضح الجدول التالي عدد المرات التي فاز فيها كل مصنف بالمباراة النهائية.

البذرة الفائزة	عدد	احتمال
1	26	65.00%
2	5	12.50%
3	4	10.00%
4	2	5.00%
5	0	0.00%
6	1	2.50%
7	1	2.50%
8	1	2.50%
من 9 إلى 16	0	0.00%
المجموع	40	100.00%

بالعودة إلى الانتصارات المتوقعة حسب التصنيف، إليكم جدول محدث، بما في ذلك البيانات من هذا الموسم.

بذرة	متوسط الانتصارات
1	3.34
2	2.33
3	1.84
4	1.56
5	1.14
6	1.06
7	0.89
8	0.73
9	0.59
10	0.61
11	0.64
12	0.51
13	0.24
14	0.16
15	0.11
16	0.01

أحد الأسئلة التي تُطرح عليّ كثيرًا هو احتمالية الحصول على قوس مثالي. بافتراض اتباع استراتيجية اختيار اللعبة الأعلى تصنيفًا (أو الرقم الأدنى) دائمًا، باستثناء الاختيار العشوائي في حالة 1 ضد 1، فإن احتماليتي المُحدّثة، بما في ذلك بيانات هذا الموسم، هي 1 من 287,548,153.

إجابة لغز المنطق

ينبغي أن تكون الإستراتيجية على النحو التالي:

1. • إذا رأيت قبعتين بألوان متعاكسة، فامرر.
2. • إذا رأيت قبعتين من نفس اللون، فاختر اللون المعاكس.

وهذا ما يمكننا أن نتوقع حدوثه وفقًا للألوان الثلاثة:

1. • ثلاثة لاعبين سود: سيشاهد جميع اللاعبين لاعبين سودًا ويصوتون للأبيض. سيكون الجميع مخطئين، وبالتالي ستفشل التجربة.
2. • قبعتان سوداوان، وقبعة بيضاء: سيشاهد اللاعب الأبيض قبعتين سوداوين، وسيصوّت بشكل صحيح للقبعة البيضاء. سيشاهد اللاعبان الأسودان قبعة من كل لون، وسيجتازان الاختبار. التجربة ناجحة.
3. • قبعة سوداء، قبعتان بيضاوان: سيشاهد اللاعب الأسود قبعتين بيضاوين، وسيصوّت بشكل صحيح للقبعة السوداء. سيشاهد اللاعبان الأبيضان قبعة من كل لون، وسيجتازان الاختبار. التجربة ناجحة.
4. • ثلاثة بيض: سيشاهد جميع اللاعبين بيضتين ويصوتون للأسود. سيكون الجميع مخطئين، وبالتالي تفشل التجربة.

احتمال وجود ثلاثة ألوان بيضاء أو ثلاثة ألوان سوداء هو 2*(1/2) ³ = 25%. البديل هو تقسيم اللونين بنسبة 2-1، باحتمال 75%. كما هو موضح أعلاه، مع تقسيم اللونين بنسبة 2-1، ستنجح التجربة.