إثبات تباعد السلسلة التوافقية

سيكون برهان هذا الأسبوع هو تقارب المتسلسلة التوافقية. ولكن قبل ذلك، أقدم لكم لغز المنطق الأسبوعي المعتاد.

لغز منطقي

يوجد يوم الاثنين طفلان في حضانة المستشفى، صبي وفتاة.

يوم الثلاثاء، انضم مولود جديد إلى العائلة.

يوم الأربعاء، يتم اختيار طفل عشوائياً. إنه صبي.

ما هو احتمال أن يكون المولود الذي ولد يوم الثلاثاء ذكراً؟

إثبات تباعد السلسلة التوافقية

المتسلسلة التوافقية هي مجموعة معكوسات جميع الأعداد الصحيحة. بعبارة أخرى، 11 ، 12 ، 13 ، 14 ،6؛ نوع الخط: 'Open Sans'، sans-serif؛ اللون: #313131 !important؛"> 1 5 ,…, 1 ∞ . يُقال إن المتسلسلة متباعدة إذا كان مجموع جميع عناصرها لانهائيًا. هذا ليس واضحًا في حالة المتسلسلة التوافقية لأن عناصرها تتناقص إلى ما لا نهاية. ومع ذلك، دعني أثبت أن المجموع لانهائي بالفعل.

الطريقة الأولى: اختبار المقارنة

إذا استطعت إثبات أن سلسلة أخرى ذات عناصر متساوية أو أقل متباعدة، فلا بد أن تكون السلسلة التوافقية متباعدة أيضاً.

السلسلة التوافقية: 1 1 ، 1 2 ، 1 3 ، 1 4 ، 1 5 ، 1 6 ،6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 7 , 1 8 , 1 9 , 1 10 , 1 11 , 1 12 , 1 13 ,…, 1 ∞ .

السلسلة 2: 1 1 ، 1 2 ،6؛ نوع الخط: 'Open Sans'، sans-serif؛ اللون: #313131 !important;"> 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 ,6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 16 , 1 16 , 1 16 , 1 32 ,…, 1 ∞ .

تبدأ السلسلة الثانية بنفس العنصرين اللذين تبدأ بهما السلسلة التوافقية. ثم، لكل n ≥ 2، تتكرر السلسلة بمقدار 1 / ²ⁿ × ^2n-1 مرة. لاحظ أن كل عنصر في السلسلة الثانية يساوي أو يقل عن نظيره في السلسلة التوافقية. يمكن تقسيم السلسلة الثانية إلى مجموعات مجموعها يساوي 1 / ²ⁿ × ^2n-1 = 1/2 . دعني أوضح ذلك بإعطاء كل مجموعة لونًا مختلفًا:

السلسلة 2: 1 1 ،6؛ نوع الخط: 'Open Sans'، sans-serif؛ اللون: #313131 !important;"> 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6؛ نوع الخط: 'Open Sans'، sans-serif؛ اللون: #00A0D1 !important;"> 1 16 ، 1 16 ، 1 16 ، 1 16 ، 1 32 (16 مرة)، 1 64 (32 مرة) …، 1 ∞

1 + ( 1 2 X ∞)= ∞

الطريقة الثانية: حساب التفاضل والتكامل

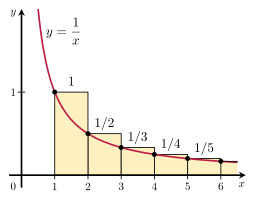
لاحظ أن مساحة المستطيلات الصفراء أكبر من المساحة تحت المنحنى الأحمر. مساحة المنحنى الأحمر هي:

∫ ₁ ^∞ 1 x dx = ln(x) + c من 1 إلى ∞ = ln(∞) + c – ln(1) – c = ∞.

حل لغز المنطق

إجابة مختصرة

هناك تفسيران محتملان لما حدث. لنسميهما س و ص.

X = تمت إضافة ولد يوم الثلاثاء، وتمت ملاحظة ولد آخر يوم الأربعاء. احتمال حدوث ذلك هو (1/2) × (2/3) = 2/6 = 1/3.

Y = تمت إضافة فتاة يوم الثلاثاء، ولوحظ وجود ولد يوم الأربعاء. احتمال حدوث ذلك هو (1/2) × (1/3) = 1/6.

س + ص = 1/3 + 1/6 = 1/2

السؤال هو ما احتمال وقوع الحدثين، حيث يمثل X الحدث الذي وقع. وبالتالي، فإن احتمال وقوع X هو X/(X+Y) = (1/3)/(1/2) = 2/3.

إجابة مطولة

تنص صيغة الاحتمال الشرطي البايزي على أن احتمال وقوع الحدث A بشرط وقوع الحدث B يساوي احتمال وقوع الحدثين A وB معًا، مقسومًا على احتمال وقوع الحدث B، حيث احتمال وقوع الحدث x هو احتمال وقوع أي حدث x. لنفترض أن:

أ = ولد تمت إضافته يوم الثلاثاء

6؛ نوع الخط: 'Open Sans'، sans-serif؛ اللون: #313131 !important؛ ">ب = صبي شوهد يوم الأربعاء

في هذه الحالة:

Prob(A given B) = Prob(Boy added on Tuesday given boy observation on Wednesday) = Prob(Boy added on Tuesday and boy observation on Wednesday)/Prob(Boy observation on Wednesday).

في حال عدم توفر معلومات عن سحب يوم الثلاثاء، فإن احتمال أن يكون المولود ذكراً هو ٥٠٪. وبافتراض أن المولود الذي تم سحبه يوم الثلاثاء كان ذكراً، فإن احتمال أن يكون المولود الذي تم سحبه يوم الأربعاء ذكراً هو ٢/٣.

وبالمثل، في حال عدم توفر معلومات عن سحب يوم الثلاثاء، فإن احتمال أن تكون المولودة أنثى في ذلك اليوم هو ٥٠٪. وبافتراض أن المولودة التي سُحبت يوم الثلاثاء كانت أنثى، فإن احتمال أن يكون المولود الذي سُحب يوم الأربعاء ذكراً هو ١/٣.

احتمال سحب ولد يوم الأربعاء يساوي احتمال (إضافة ولد يوم الثلاثاء) * احتمال (سحب ولد يوم الأربعاء) + احتمال (إضافة بنت يوم الثلاثاء) * احتمال (سحب ولد يوم الأربعاء) = (1/2) * (2/3) + (1/2) * (1/3) = 1/2.

احتمالية إضافة ولد يوم الثلاثاء وسحب ولد يوم الأربعاء = (1/2)*(2/3) = 1/3.

وبالتالي، فإن الإجابة هي (1/3)/(1/2) = 2/3.