جدولة الدوري

موضوع هذا الأسبوع هو كيفية جدولة بطولة بنظام الدوري. قبل أن أتعمق أكثر، نظام الدوري هو نظام بطولة يلعب فيه كل لاعب ضد لاعب آخر. في بطولة تضم n لاعبًا، يكون عدد المباريات n(n-1)/2.

من السهل سرد جميع الثنائيات المحتملة n(n-1)/2 بين n لاعب. مع ذلك، يُفضل القيام بذلك في جولات، حيث يلعب كل لاعب مرة واحدة في كل جولة. إليك كيفية القيام بذلك مع عدد زوجي من اللاعبين. لنأخذ حالة الثمانية لاعبين كمثال. في الصورة التالية، نُسمّي اللاعبين من A إلى H، ونُظهر اللاعبين في مباراة داخل المستطيلات الأربعة. تُشكّل هذه المباريات الأربع الجولة الأولى. لاحظ كيف يلعب الجميع.

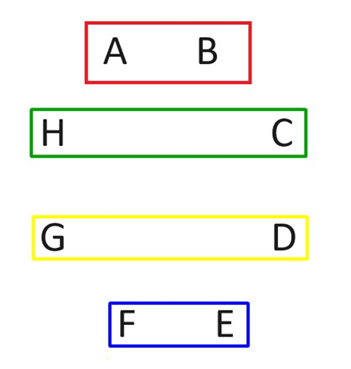
في الجولة الثانية، أبقِ اللاعب أ في نفس موقعه. ثم أدر جميع اللاعبين الآخرين باتجاه عقارب الساعة، كما هو موضح في الرسم التخطيطي التالي.

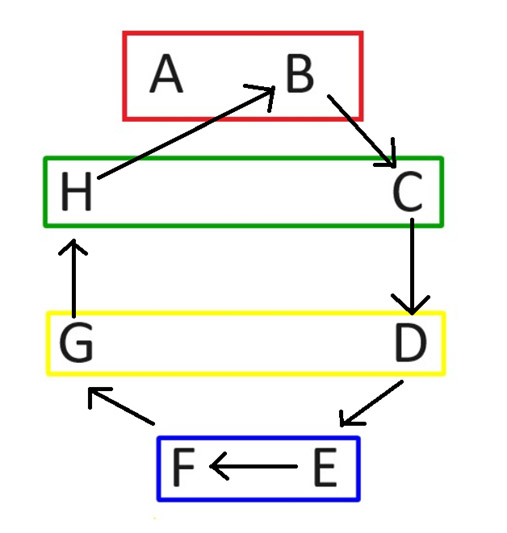
وبعد التدوير، ستكون مباريات الجولة الثانية على النحو التالي:

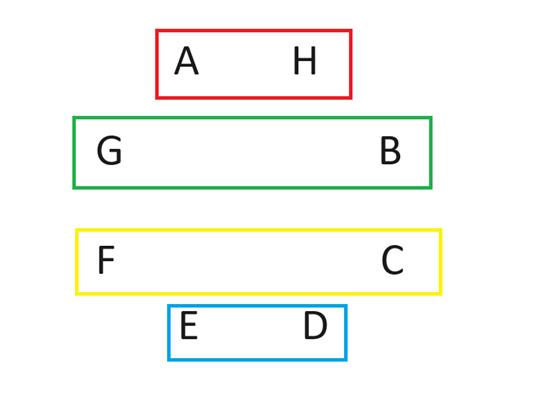
استمر في فعل ذلك حتى يلعب الجميع ضد اللاعب أ. لا أستطيع شرح سبب نجاح هذه الطريقة، لكنها تنجح ببساطة. تُجدي نفعًا مع أي عدد زوجي من اللاعبين. لمزيد من النقاش حولها، ابحث عن "طريقة الدائرة" و"دورة روبن".

يوضح الجدول التالي جميع المباريات في حالة الثمانية لاعبين. لاحظ كيف يلعب كل لاعب ضد الآخر مرة واحدة فقط.

دائري	اللاعب 1	اللاعب 2
1	أ	ب
1	ح	ج
1	ج	د
1	ف	هـ
1	أ	ح
2	ج	ب
2	ف	ج
2	هـ	د
3	أ	ج
3	ف	ح
3	هـ	ب
3	د	ج
4	أ	ف
4	هـ	ج
4	د	ح
4	ج	ب
5	أ	هـ
5	د	ف
5	ج	ج
5	ب	ح
6	أ	د
6	ج	هـ
6	ب	ف
6	ح	ج
7	أ	ج
7	ب	د
7	ح	هـ
7	ج	ف

إذا كان عدد اللاعبين فرديًا، يكفي إضافة لاعب وهمي إلى البطولة للحصول على عدد زوجي. من يلعب ضد اللاعب الوهمي يحصل على إعفاء في تلك الجولة، أي أنه يتغيب عن اللعب. وبالتالي، سيُمنح الجميع جولة واحدة حيث لا يشاركون. هكذا يبدو الأمر في بطولة مكونة من سبعة لاعبين.

دائري	اللاعب 1	اللاعب 2
1	أ	ب
1	الوداع	ج
1	ج	د
1	ف	هـ
2	أ	الوداع
2	ج	ب
2	ف	ج
2	هـ	د
3	أ	ج
3	ف	الوداع
3	هـ	ب
3	د	ج
4	أ	ف
4	هـ	ج
4	د	الوداع
4	ج	ب
5	أ	هـ
5	د	ف
5	ج	ج
5	ب	الوداع
6	أ	د
6	ج	هـ
6	ب	ف
6	الوداع	ج
7	أ	ج
7	ب	د
7	الوداع	هـ
7	ج	ف

أخيرًا، لنفترض أن هذه بطولة تنس، ولكل ملعب جانب جيد وآخر سيئ. من المحتمل أن يكون الجانب السيئ مواجهًا للشمس. ما هي الطريقة العادلة لضمان تساوي عدد مرات ظهور الجوانب الجيدة والسيئة لكل لاعب؟

لحل هذه المشكلة، أقترح استخدام " توسعة ليزارد سبوك "، كما هو موضح في نظرية الانفجار العظيم. تعمل هذه الطريقة للعب حجرة ورقة مقص مع أي عدد فردي من الرموز. لتحديد اللاعب الذي يحصل على الجانب الجيد بدقة، لنأخذ حالة اللاعبين السبعة. يوضح الرسم البياني التالي اللاعب الذي يحصل على الجانب الجيد، كما هو موضح بالسهم الذي يشير إلى اللاعب الذي يحصل على الجانب السيئ.

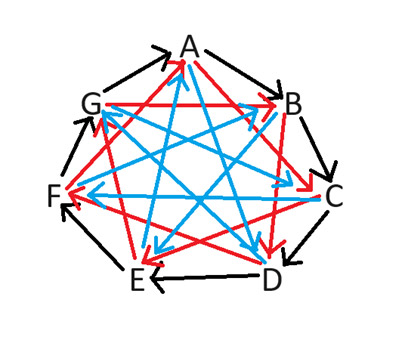
على سبيل المثال، إذا لعب اللاعبان ب و د، سيحصل ب على الجانب الجيد، لأن السهم بينهما يشير إلى د. ليس من الصعب فهم كيفية رسم المخطط. تشير الأسهم دائمًا باتجاه عقارب الساعة. يجب رسمها لكل عدد ممكن من الفجوات من ١ إلى ٣.

مع ذلك، ليس من الضروري رسم مثل هذا المخطط، بل حلقة من الحروف فقط. فكّر في كلا الطريقتين للدوران حول الدائرة باتجاه عقارب الساعة للانتقال من لاعب إلى آخر. الطريقة الأقل خطوات هي التي تحصل على الجانب الجيد. لنفترض وجود لعبة بين B وF. عند الدوران باتجاه عقارب الساعة، تكون المسافة من B إلى 4 أربع خطوات، ومن F إلى B ثلاث خطوات. بما أن ثلاثة أقل من أربعة، فإن F يحصل على الجانب الجيد.

يوضح الجدول التالي جميع المباريات الممكنة في دورة روبن مكونة من سبعة لاعبين، بما في ذلك اللاعبين الذين يحصلون على الجانبين الجيد والسيئ.

دائري	الجانب الجيد	الجانب السيئ
1	أ	ب
1	ج	الوداع
1	د	ج
1	هـ	ف
2	أ	الوداع
2	ج	ب
2	ج	ف
2	د	هـ
3	ج	أ
3	ف	الوداع
3	ب	هـ
3	ج	د
4	ف	أ
4	هـ	ج
4	د	الوداع
4	ب	ج
5	هـ	أ
5	د	ف
5	ج	ج
5	ب	الوداع
6	أ	د
6	ج	هـ
6	ف	ب
6	ج	الوداع
7	أ	ج
7	ب	د
7	هـ	الوداع
7	ف	ج

للأسف، لا تُجدي استراتيجية موازنة الجوانب هذه نفعًا مع عدد زوجي من اللاعبين. ذلك لأن المسافتين متساويتان حول الدائرة عندما يكون اللاعبان على جانبين متقابلين تمامًا. إذا اضطررت لذلك، يُمكن استخدام هذه الطريقة في جميع المواجهات الأخرى، ولكن سيتعين على اللاعبين اختيار اللاعبين عشوائيًا عندما يكونون على بُعد 180 درجة على الدائرة.

هذا كل ما سأتناوله في هذا الموضوع حاليًا. أحتفظ بحق التوسّع فيه في نشرة إخبارية مستقبلية. من المواضيع المحتملة لمزيد من النقاش المباريات التي تضم ثلاثة لاعبين أو أكثر، بالإضافة إلى استخدام ملاعب متعددة حيث يُفضّل موازنة عدد مرات لعب كل لاعب على كل ملعب.

وفي الختام، أتمنى لكم جميعا عيد حانوكا سعيدًا!

كتبه: Michael Shackleford