نظرية مجموع زوايا المثلث يساوي 180 درجة

من المعروف أن مجموع الزوايا الداخلية لأي مثلث يساوي ١٨٠ درجة. في هذه النشرة الإخبارية، سأقدم برهانًا بسيطًا. ولكن قبل ذلك، سأقدم لغز المنطق الأسبوعي المعتاد.

لغز المنطق

لدى ملك ٤٩ قطعة ذهبية. وزن كل قطعة ١، ٢، ٣، ... ٤٩ غرامًا. كيف يُقسّمها على سبعة أبناء بحيث يحصل كل ابن على سبع قطع ذهبية، بحيث يكون مجموع الأوزان متساويًا؟

دليل على أن مجموع الزوايا الداخلية لأي مثلث يساوي 180 درجة.

سأبدأ برسم مثلث عشوائي وتسمية الزوايا.

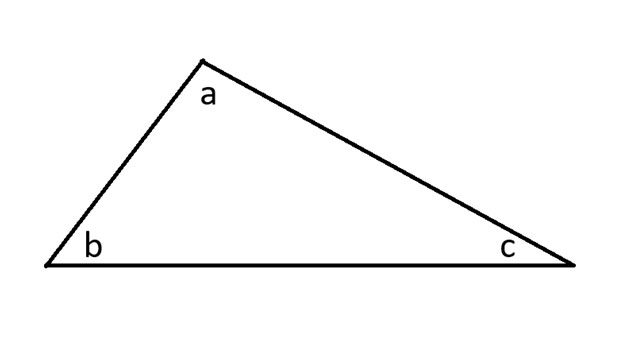
بعد ذلك، سأقوم بتمديد جميع الأضلاع الثلاثة للمثلث بالإضافة إلى رسم خط موازٍ يلامس الزاوية أ.

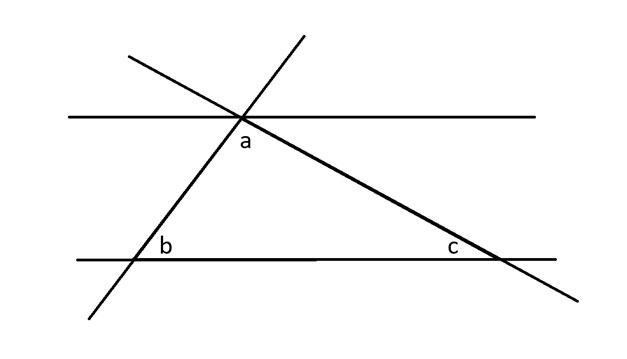
بعد ذلك، سأطبق نظرية الزاوية المعاكسة على الزاوية ب، والتي تقول إن الزوايا عند الزوايا المتقابلة لخطين متقاطعين متساوية.

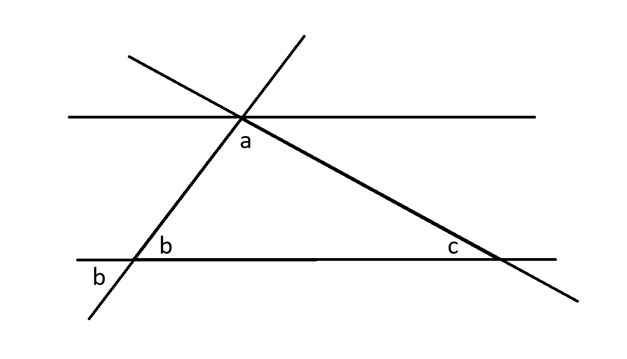
عندما يقطع قطرٌ مجموعةً من الخطوط المتوازية، فإنه يُكوّن نفس الزوايا عند تقاطعه مع كل خط. أطبّق ذلك لإظهار زاوية أخرى قياسها ب درجة بجوار الزاوية أ. ثم أفعل الشيء نفسه مع الزاوية ج.

6؛ عائلة الخطوط: 'Open Sans'، sans-serif؛ اللون: #313131 !important; ">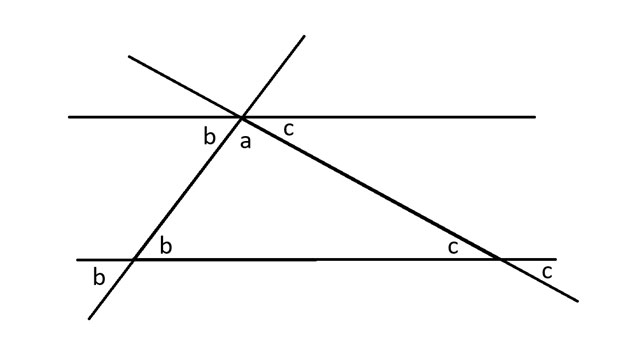

هناك ٣٦٠ درجة في الدائرة. وبالتالي، هناك ١٨٠ درجة في نصف الدائرة. بمعنى آخر، بالنظر إلى الزوايا في أسفل الخط الموازي العلوي، فإن أ + ب + ج = ١٨٠ درجة. هذه هي أيضًا زوايا المثلث الأصلي. وبالتالي، فإن مجموع زوايا المثلث يساوي ١٨٠ درجة.

حل لغز المنطق

اصنع مربعًا سحريًا، وأعطِ كل ابن عملات معدنية في أي عمود. يمكنك أيضًا تقسيم العملات المعدنية إلى صفوف. قد تسأل: "كيف تصنع مربعًا سحريًا ٧×٧؟". تُعرف الطريقة التالية باسم الطريقة السيامية، وقد اكتُشفت في الهند منذ زمن بعيد.

لنبدأ بشبكة مُسمّاة مثل لوحة سفينة حربية مقاس 7 × 7.

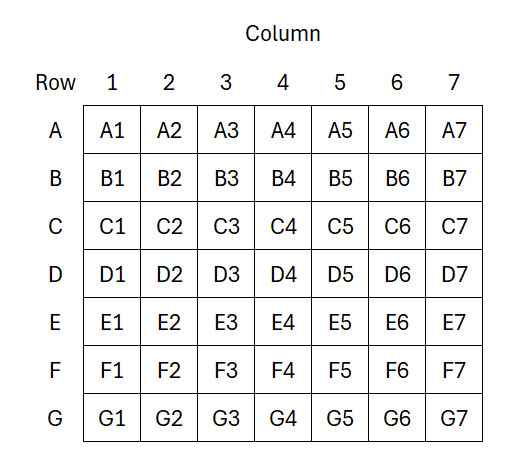
ابدأ بالرقم ١ في الخلية A4. ثم اتبع القواعد التالية:

1. أضف دائمًا 1 إلى الرقم السابق للوضع التالي.
2. اذهب دائمًا في اتجاه الشمال الغربي، إلا إذا كانت تلك المساحة مشغولة أو كنت بالفعل في الصف A أو العمود 7.
3. إذا كنت في الصف A، فانتقل إلى العمود G للرقم التالي.
4. إذا كنت في العمود 7، فانتقل إلى العمود 1 للحصول على الرقم التالي.
5. ستؤدي المكالمة A7 إلى التفاف كلا الاتجاهين إلى G1.
6. إذا كان المربع التالي الذي يجب عليك الذهاب إليه مشغولاً، فانتقل إلى المربع التالي للرقم التالي (يجب أن يكون فارغًا).

وهنا كيف نبدأ:

1. 1 في الخلية A4.
2. نحن في الصف A، لذا قم باللف إلى الصف G، ووضع 2 في الخلية G5.
3. ثم نضع 3 في F6، 4 في E7.
4. نحن في العمود 7، لذا نلتف حوله، ونضع 5 في D1.
5. ضع 6 في C2، 7 في B3.
6. ثم نأتي إلى A4، ولكنها مشغولة بالرقم 1. لذا، ننزل ونضع الرقم التالي، وهو 8، في C3.
7. استمر في التكرار حتى يمتلئ المربع السحري.

وهذا هو الشكل الذي سيبدو عليه الأمر عند الانتهاء منه:

jpg" />

ستعمل هذه الطريقة مع أي مربع سحري ذي أبعاد فردية.

ثم، حدد ما إذا كنت ستقسم حسب الصفوف أم الأعمدة. كل واحد من العملات الموجودة في أحد الصفوف/الأعمدة هو ابن العملة. على سبيل المثال، إذا قسمت حسب الأعمدة، سيحصل الابن 1 على العملات التالية: 30، 38، 46، 5، 13، 21، و22.